2. Пропорциональные отрезки в прямоугольном треугольнике.

Дата: 2025-06-02; Просмотры: 15
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Билеты по геометрии 8 класс, 2023 год

Билет №1

1. Параллелограмм (определение, свойства, признаки). Доказать: в параллелограмме противоположнее стороны и углы равны.

2. Пропорциональные отрезки в прямоугольном треугольнике.

3. Найти диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см2.

Билет №2

1. Трапеция (определение, виды, свойства равнобедренной трапеции). Доказать: в равнобедренной трапеции диагонали равны.

2. Соотношения между сторонами и углами прямоугольного треугольника (определение синуса, косинуса, тангенса острого угла прямоугольного треугольника, формулы)

3. В прямоугольной трапеции основания равны 5 и 17 см, а большая боковая сторона 13 см. Найти площадь трапеции.

 

 

Билет №3

1. Прямоугольник (определение, свойства). Доказать: диагонали прямоугольника равны.

2. Свойства биссектрисы угла, серединного перпендикуляра к отрезку

3. Найти сторону квадрата, площадь которого равна площади прямоугольника со смежными сторонами 8 см и 18 см.

 

 

Билет №4

1. Ромб (определение, свойства). Доказать: диагонали ромба взаимно-перпендикулярны и делят его углы пополам.

2. Таблица значений синуса, косинуса, тангенса углов 30°, 45°, 60°.

3. В трапеции АВСD с большим основанием AD диагональ АС перпендикулярна к боковой стороне СD, 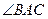= 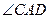. Найти АD, если периметр АВСD равен 20 см, а 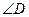= 60°.

 

 

Билет №5

1. Квадрат (определение, свойства). Доказать: ромб, у которого один угол прямой, является квадратом.

2. Четыре замечательные точки треугольника.

3. В треугольнике два угла равны 45° и 90°, а большая сторона 20 см. Найти две другие стороны.

 

 

Билет №6

1. Площадь многоугольника, свойства. Площадь квадрата, прямоугольника (формулы). Доказать: теорему о площади параллелограмма S = ah

2. Признаки равенства треугольников, прямоугольных треугольников.

3. Найти площадь равнобедренной трапеции, если известно, что ее основания равны 10 см и 24 см, а боковая сторона равна 25 см.

 

Билет №7

1. Треугольник (определение, виды треугольников). Вывести формулу площади треугольника S = 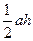. Назвать две формулы площади для треугольников.

2. Свойства хорд, пересекающихся внутри окружности и двух касательных.

3. Стороны АВ и ВС треугольника АВС равны соответственно 16 и 22 см., а высота, проведенная к стороне АВ, равна 11 см. Найти высоту, проведенную к стороне ВС.

 

 

Билет №8

1. Трапеция (определение, виды). Вывод формулы площади трапеции.

2. Теоремы об отношении площадей подобных треугольников; треугольников, имеющих по равному углу; треугольников, имеющих равные высоты.

3. Точки D и E лежат на стонах АВ и АС треугольника АВС. Найти 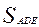, если АВ = 5 см, АС = 6 см, AD = 3 см, AE = 2 см. 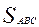= 10 см2.

 

 

Билет №9

1. Прямоугольный треугольник. Доказательство теоремы Пифагора.

2. Касательная к окружности (определение, свойство, признак).

3. Диагонали ромба равны 14 и 48 см. Найти сторону ромба.

 

 

Билет №10

1. Подобные треугольники (определение, коэффициент подобия, признаки подобия). Доказательство признака по двум углам.

2. Центральные и вписанные углы (определение, свойства).

3. Вершины треугольника АВС лежат на окружности с центром в точке О, 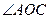= 80°, 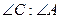= 3:4. Найти градусные меры дуг АВ, АС, ВС.

Билет №11

1. Теорема о биссектрисе угла треугольника (доказательство) (задача №535).

2. Формулы площадей четырехугольников (параллелограмм, прямоугольник, ромб, квадрат, трапеция).

3. Найти периметр ромба АВСD, в котором 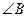=60°, АС=10,5 см.

 

 

Билет №12

1. Теорема о средней линии треугольника (доказательство).

2. Теорема Фалеса. Деление отрезка на n равных частей (задача №385, 396)

3. Стороны треугольника относятся как 4:5:6, а периметр треугольника, образованного его средними линиями равен 30 см. Найти средние линии треугольника.

 

 

Билет №13

1. Свойство о медианах треугольника (доказательство).

2. Признаки параллельности прямых.

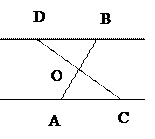
3. На рисунке АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, OD = 6,3 см. Докажите, что АС || BD.Найдите: а) DB : АС; б)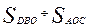

 

 

Билет №14

1. Свойства прямоугольного треугольника. Доказать свойство прямоугольного треугольника с углом в 30⁰.

2. Свойства углов при параллельных прямых.

3. Найти периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.