Расчет интерференционной картины от двух когерентных источников

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

9. Классические интерференционные опыты (опыт Юнга, зеркала Френеля, бипризма Френеля). Расчет интерференционной картины от двух цилиндрических волн.

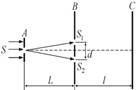Опыт Юнга

Образование интерференционной картины можно наблюдать в рассмотренном опыте Юнга, использующем метод деления волнового фронта.

Прошедший через узкую длинную щель S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя, параллельными между собой узкими щелями S₁ и S₂, расположенными близко друг к другу на равных расстояниях от S. Эти щели действуют как вторичные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Расстояние между соседними полосами равно: 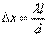Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными.

Зеркала Френеля

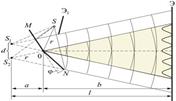Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу.

Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой . Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источникам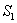и и 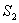, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на 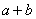, где 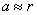- расстояние от S до ребра зеркал, b - расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно: 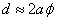. Поэтому ширина интерференционной полосы на экране равна: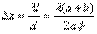

Бипризма Френеля

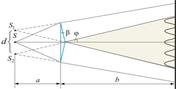В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы. Можно считать, что здесь образуются два близких мнимых изображения S₁ и S₂ источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол .

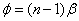Расчет интерференционной картины от двух когерентных источников

Пусть имеется два когерентных источника S1 и S2 в виде двух узких длинных параллельных щелей, лежащих в одной плоскости и расположенных в воздухе (w=l) на расстоянии D друг от друга. Экран, на котором наблюдается интерференцион­ная картина, расположен в плоскости, параллельной плоскости источников, на расстоянии L от нее/S1и S2 являются ис­точниками волн с цилиндрическим фронтом частотой со. На экра­не в области перекрытия световых пучков АВ (называемой полем интерференции) наблюдается интерференционная картина в виде полос, параллельных щелям

Рассчитаем интенсивность результирующего колебания в произвольной точке М, отстоящей на расстоянии х от оси сим­метрии системы Будем считать, что амплитуды свето­вых волн от источников S1 и S2 одинаковы и равны Ео.

Тогда колебания, дошедшие в точку М, будут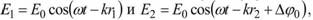

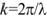
где г\ и г2 - расстояния от точки М до источников S\ и Si,

волновое число, Аф0 - начальная разность фаз световых волн, ис­пускаемых источниками S\ и Si.

Складываясь в точке М, колебания дадут

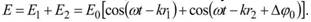
Воспользовавшись известной тригонометрической формулой преобразования суммы косинусов двух углов, получим

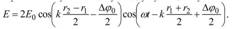
В только последний сомножитель описывает волновой процесс, следовательно, это выражение можно переписать в следующем виде:

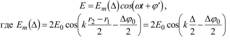
амплитуда колебании в точке М, а ср - начальная фаза колеба­ний. Согласно (1.12) интенсивность световых колебаний в точке М будет

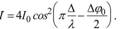
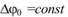
(источники S1 и S2 когерентные), то интенсивность результирующего колебания будет зависеть только от разности хода 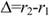, из-за наличия которой между лучами, дошедшими до точки М, возникает разность фаз 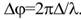тогда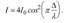

Если 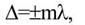где m=0,1,2,3... - целое число, называемое порядком интерфе­ренции, то разность фаз оказывается кратной 2m, колебания в точке М будут происходить в фазе - наблюдается максимум ин­тенсивности.

Если 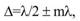то световые волны до точки М дойдут в противофазе - наблюда­ется минимум интенсивности.Рассчитаем основные характеристики интерференционной картины, т.е. положение максимумов и минимумов на экране и их периодичность. Будем попрежнему считать, что показатель преломления среды n=1 .Видно, что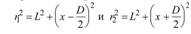

тогда 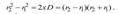Но обычно при наблюдении интерференционных картин выпол­няется соотношение D«x«L , тогда можно считать, что r1+r2~2L и получаем

Находим координаты точек, где будут наблюдаться максимумы интенсивности 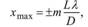координаты минимумов интен­сивности: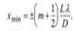

Расстояние между соседними максимумами или минимумами на­зовем шириной интерференционной полосы: 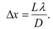Видно, что расстояние между интерференционными по­лосами увеличивается с уменьшением расстояния между источ­никами D. Для того, чтобы интерференционная картина наблю­далась отчетливо, необходимо выполнение условия D«L.

10. Интерференция света на плоскопараллельной пластине. Полосы равного наклона.