Определение коэффициента внутреннего трения воздуха
Муромский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича и
Николая Григорьевича Столетовых»
Кафедра: «ФПМ»
Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА № 6.05
Определение коэффициента внутреннего трения воздуха
и средней длины свободного пробега его молекул
Утверждено на методическом
семинаре кафедры ФПМ
Зав. кафедрой ____________
Лабораторная работа № 6.05
Определение коэффициента внутреннего трения воздуха
и средней длины свободного пробега его молекул
ЦЕЛЬ РАБОТЫ: Изучение одного из методов измерения коэффициента внутреннего трения (вязкости) газов (воздуха).
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: Установка для измерений, секундомер, сосуд для сбора воды.
Вопросы для подготовки к выполнению лабораторной работы.
1. Ознакомьтесь с устройством и принципом действия установки.
2. Изучите методику измерений.
3. На чём основано измерение коэффициента вязкости воздуха в данной работе?
4. Как вы понимаете механизм вязкости газов?
5. Что называется коэффициентом вязкости газов? От чего он зависит?
6. Что называется градиентом скорости?
7. Составьте таблицу для записи результатов измерений.
8. Как оценить ошибки измерений?
Задание к работе
1. Выполните необходимые измерения не менее 5 раз.
2. Вычислите по данным измерений не менее 5-и значений коэффициента вязкости η
3. Найдите среднюю скорость V молекул воздуха при комнатной температуре.
4. Вычислите коэффициент вязкости η и среднюю скорость молекул воздуха, вычислите среднюю длину свободного пробега его молекул λ.
5. Зная среднюю длину свободного пробега λ молекул воздуха, вычислите их эффективный диаметр d .
Дополнительные задания (по указанию преподавателя)
1. Зная λ и эффективный диаметр молекул воздуха, вычислите число его молекул в 1 см3 и в 1 м3.
2. Вычислите массу одного киломоля и коэффициент диффузии воздуха.
3. Вычислите число столкновений молекул воздуха за 1 сек. и найдите его коэффициент теплопроводности.
4. Вычислите удельные теплоёмкости воздуха СP и СV, давление атмосферы по вашим измерениям.
5. Вычислите кинетическую энергию молекул в 1 см3 воздуха при температуре ваших опытов.
6. Вычислите коэффициенты диффузии и теплопроводности воздуха.
Внутреннее трение (вязкость) наблюдается во всех агрегатных состояниях вещества при перемещении его слоёв относительно друг друга.
Рассмотрим механизм внутреннего трения в газах.
Представим себе, что газ движется по трубе так, что можно легко выделить очень тонкие слои газа, движущиеся относительно стенок трубы с разными скоростями ū (рис.1).
Молекулы газа прилипают к стенкам трубы и поэтому граничный слой практически не пере 
мещается. По мере удаления от стенок трубы скорость слоёв газа будет возрастать и достигать наибольшего значения на оси трубы.
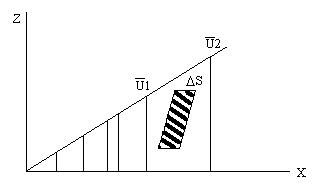
Рис. 1
Между слоями жидкости действуют более или менее значительные силы внутреннего трения. Эта сила может быть найдена по формуле:
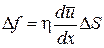(1)
где η – коэффициент вязкости (внутреннего трения),
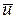– скорость движения газа,
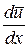– градиент скорости,
ΔS – площадь соприкосновения двух слоёв газа, на которую действует сила Δf.
Рассмотрим явление внутреннего трения с позиций молекулярно-кинетической теории газов.
Молекулы газа, протекающие по трубе, участвуют в двух движениях: в беспорядочном тепловом с некоторой скоростью V и в направленном по трубе со скоростью соответствующего слоя ū.
Положим, что все молекулы газа имеют одинаковую среднюю скорость V и одинаковую массу m.
Рассмотрим два соседних слоя газа, движущихся со скоростями ū1 и ū2. На границе слоёв выделим площадку ΔS (рис. 1). Каждая молекула газа обладает импульсом m(V + ū). Поскольку V по нашему предположению одинакова для всех молекул газа, то различие импульсов молекул разных слоёв определяется различием скоростей этих слоёв.
Вследствие беспорядочности теплового движения молекул газа, они будут переходить из одного слоя в другой. При переходе из слоя движущегося с большей скоростью ū2, в слой с меньшей скоростью ū1 каждая молекула будет передавать вследствие столкновений молекулам последнего некоторый добавочный импульс (m·ū2 – m·ū1) и, тем самым, будет ускорять более медленный слой. При переходе из более медленного слоя в более быстрый слой молекулы получают от него добавочный импульс (m·ū2 - m·ū1) и тем самым притормаживают более быстрый слой.
Таким образом, между слоями движущегося газа непрерывно происходит обмен импульсов, что приводит к возникновению силы взаимодействия между слоями. Это и будет сила внутреннего трения. Найдём значение этой силы, действующей на площадку между выделенными слоями (рис. 1).
В среднем по оси OX в каждой единице объёма газа движется 1/3n молекул. Очевидно, что через площадку слева направо за Δt пройдёт:
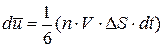
молекул, которые переносят импульс: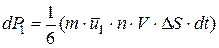 
(2)
молекулы, пролетающие через ΔS справа налево, переносят импульс:
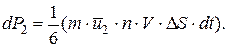(3)
Вследствие теплового движения молекул газа через площадку переносятся за dt импульс.
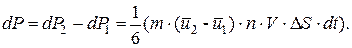(4)
Сила внутреннего трения, приложенная к площадке равна:
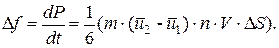(5)
Очевидно, через выделенную площадку ΔS вероятнее всего пройдут молекулы, находящиеся от неё на расстоянии, не превышающем средней длины их свободного пробега. Выразим скорости ū1 и ū2 так:
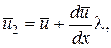
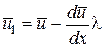(6)
Учтём, что произведение числа молекул n в единице объёма на массу m одной молекулы есть плотность газа ρ = n·m. С учётом (6) формула (5) примет вид:
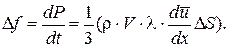(7)
Сравнивая (7) с(1) получим, что
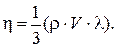(8)
Таким образом, на основе молекулярно-кинетической теории получена формула для вычисления коэффициента вязкости газа.
Эксперимент
Для определения коэффициента вязкости воздуха в данной работе используется капиллярный вискозиметр (Рис. 2). Он состоит из аспиратора А с краном К и пробкой В, соединённого трубками с водяным манометром М и капилляром С. С капилляром соединен осушительный фильтр или трубка Ф, сообщающаяся с другим коленом манометра М. В аспиратор наливается вода. Открыв кран К, из аспиратора вытекает вода. Через капилляр С и трубку Ф протекает воздух. Вытекающая вода собирается в сосуд Д.
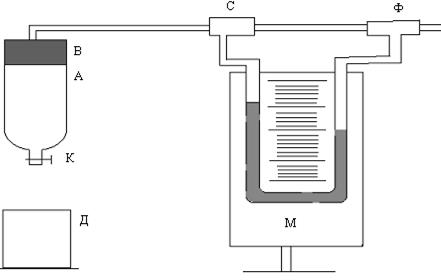
Рис 2.
При этом на концах капилляра С возникает разность давлений ΔР, которая устанавливается формулой Пуазейля:
)
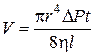
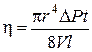где, r = 0,2 мм – радиус капилляра;
l = 9,8 мм – его длина.
Объём воздуха V , прошедшего за время t через капилляр С, определяется по шкале, нанесённой на аспираторе. Как видно из (9) для измерения коэффициента вязкости воздуха необходимо измерить объём воды, вытекающей за время t из аспиратора при закрытом пробкой его верхнем конце, а также разность давлений ΔР на концах капилляра. Для этого при закрытом кране К вынимают пробку В, наполняют аспиратор водой. Закрывают аспиратор пробкой В и осторожно открывают кран К, выпуская воду тонкой струйкой. Выжидают некоторое время, пока установится стационарное течение воздуха через капилляр, включают секундомер и измеряют время t, объём V и разность ΔР. Результаты измерений заносят в таблицу.
Вычисление средней длины свободного пробега молекул воздуха
и эффективного диаметра его молекул.
Вычислив η по формуле (9) и оценив ошибки измерений по формуле (8) вычисляют λ.
Средняя длина свободного пробега молекул газа λ оценивается формулой:
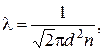(10)
где, d – эффективный диаметр молекулы,
n – число молекул в единице объёма (в 1 м3), его можно вычислить по формуле:
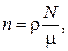
где N – число Авогадро,
ρ = 1,29 кг/м3 – плотность воздуха,
µ – масса одного киломоля воздуха µ = 29 кг/кмоль.
Средняя длина свободного пробега молекул вычисляется по формуле:
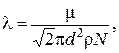(12)
Из (12) найдите d.
Контрольные вопросы
1. Какие явления переноса вы знаете?
2. Чем обусловлено явление диффузии?
3. Каков механизм теплопроводности с точки зрения молекулярно-кинетической теории газов?
4. Дайте характеристику методам и измерениям используемым в данной работе.
Литература
1. И.В. Савельев «Курс общей физики» т. I изд. Наука ГРФМЛ, 1977г. гл. 16 § 128-130
2. Г.А. Зисман и Д.М. Тодео. «Курс общей физики» т. I стр. 138-135.