Изучение второго начала термодинамики и определение приращения энтропии
Муромский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича и
Николая Григорьевича Столетовых»
Кафедра: Физика
Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА № 6.04
ИЗУЧЕНИЕ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ И ОПРЕДЕЛЕНИЕ ПРИРАЩЕНИЯ ЭНТРОПИИ
Утверждена на методическом семинаре кафедры ФПМ
________________Зав. кафедрой
ТЕХНИКА БЕЗОПАСНОСТИ
1. Проверить правильность сборки схемы.
2. Убедиться в исправности приборов.
3. В процессе работы не дотрагиваться руками до тигеля, т.к. находящееся в нем олово нагревается до температуры 2310С.
4. Не дотрагиваться руками до открытых токоведущих частей схемы.
ИЗУЧЕНИЕ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ И ОПРЕДЕЛЕНИЕ ПРИРАЩЕНИЯ ЭНТРОПИИ.
ЦЕЛЬ РАБОТЫ: построить кривую нагревания олова и найти соответствующее приращение энтропии.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: тигель с оловом, термопара, ртутный термометр, милливольтметр, сосуд с водой.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Любая термодинамическая система состоит из большого числа микрочастиц и является системой макроскопической. Для такой системы принято различать макроскопические и микроскопические состояния. Макросостояние системы определяется макроскопическими параметрами. Это – давление Р, температура Т, объем V и т. п. Они характеризуют систему как единое целое. Микросостояние системы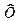 
определяется значением координаты и импульса (скорости) частицы системы.
,
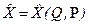где Q – координата частицы,
Р –импульс частицы.
Макросостояние описываются параметрами P, V, T. Оно может оставаться неизменным в течение большого промежутка времени. Однако, вследствие беспорядочного движения координаты и импульсы частиц системы непрерывно изменяются. Следовательно, непрерывно изменяется большое число микросостояний. Число микросостояний, соответствующих данному макросостоянию, называется статистическим весом или термодинамической вероятностью W этого макроскопического состояния. Очевидно, что статистический вес можно рассматривать как одну из важнейших характеристик теплового состояния термодинамической системы. Именно статистический вес связывает макросостояние системы с ее микросостоянием. Однако, статистический вес оказывается неудобной характеристикой макросостояния, так как является не аддитивной величиной.
Принято на практике применять другую величину, пропорциональную натуральному логарифму статистического веса макросостояния:
S = K · ln W, (1)
где S – энтропия термодинамической системы,
К – постоянная Больцмана, равная 1,38·10-23 Дж/К.
Из изложенного выше следует, что термодинамическая вероятность определяет степень беспорядочности теплового движения частиц системы:
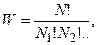
где N – число молекул в данной системе,
N1 – число молекул со скоростями u1,
N2 – число молекул со скоростями u2, и т.д.
И энтропия этой системы может служить мерой беспорядочности движения частиц.
Методом статистической физики можно вычислить для многих термодинамических систем их статистические веса и их энтропию. Однако, изменение энтропии можно вычислить на основе законов термодинамики. Энтропия любой макроскопической системы является функцией состояния, дифференциал которой равен элементарному количеству теплоты, деленному на абсолютную температуру, при которой эта теплота сообщается системе:
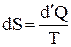. (2)
Уравнение (2) справедливо для обратимых процессов. Как известно, абсолютное (подавляющее) большинство процессов в природе являются необратимыми. Для необратимых процессов:
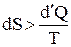. (3)
Объединяя (2) и (3), получим:
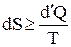. (4)
Уравнение (4) можно рассматривать как математическую формулу второго начала термодинамики. Если же система замкнутая, слабо взаимодействующая с внешними силами, то можно считать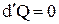 
. Тогда же из (4) следует:
dS = 0. (5)
Энтропия замкнутой (изолированной) системы не может убывать. Она остается неизменной. Полученный вывод является одной из возможных формулировок второго начала термодинамики. Так как тепловые процессы в разомкнутой системе необратимы, то из (4) получим:
dS > 0.
Это означает, что процессы, происходящие в разомкнутой системе, сопровождаются возрастанием энтропии. Возрастание энтропии в данном случае связано с переходом системы в равновесное состояние. Но равновесному состоянию соответствует наибольший статистический вес. Поэтому процессы в разомкнутой системе протекают в направлении перехода ее из менее вероятных неравновесных состояний в, соответственно, более вероятные – равновесные с наибольшей термодинамической вероятностью. Следовательно, второе начало термодинамики определяет направление протекания самопроизвольных процессов в природе.
На основе соотношения (4) найдем приращение энтропии при нагревании и плавлении металла и при следующем нагревании жидкого металла. Интегрируя (4), имеем:
.
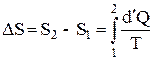Подсчитаем количество теплоты, необходимое для нагревания металла от температуры Т1 до температуры плавления Тпл:
dQ1 = mcdT;
.
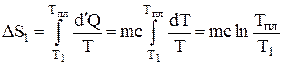Далее металл плавится при Т = Тn1 = const. Приращение энергии DS2 при плавлении:
.
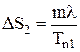Наконец приращение энтропии при нагревании расплавленного металла до температуры Т2:
,
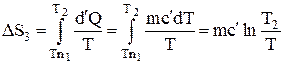Здесь m – масса металла,
с – его удельная теплоемкость,
l – удельная теплота плавления,
с’ – удельная теплоемкость жидкого металла.
Полагая с = с’, найдем суммарное приращение энтропии:
DS = DS1 + DS2 +DS3,
,
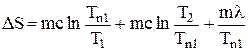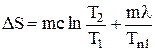. (6)
Формула (6) является расчетной для данной лабораторной работы. В работе используется олово. Его масса m = 240 г, удельная теплоемкость с = 230 Дж/кгК, удельная теплота плавления l = 5,86*104 Дж/кг.
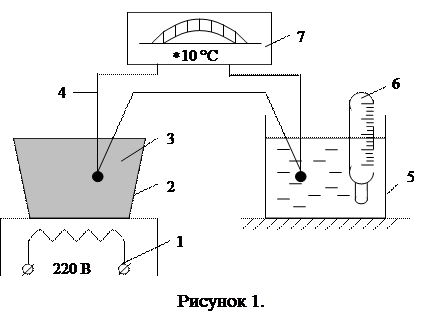
ОПИСАНИЕ УСТАНОВКИ.
Работа выполняется на установке, схема которой приведена на рис. 1. Она состоит из нагревателя 1, тигеля 2 с металлом 3, термопары 4, один спай которой находится при постоянной температуре в калориметре 5 с водой. Температура воды в калориметре определяется по ртутному термометру 6. Термопара подключена к милливольтметру 7, одна из шкал которого проградуирована в градусах Цельсия. С помощью термопары определяется температура металла в процессе его нагревания. Однако, следует заметить, что милливольтметр показывает не истинную температуру металла, а разность температур металла и жидкости в калориметре. Поэтому при нагревании металла его температуру tм надо определять по формуле:
tм = tэ + tр, (7)
 |
где tэ – температура по шкале милливольтметра,
tр – показания ртутного термометра.
Абсолютные температуры, входящие в формулу (6), вычисляются по формулам:
Т1 = tр + 273°С, Т2 = tэ2 + tр + 273°С, Тn1 = tэn1 + tр + 273°С. (8)
ВЫПОЛНЕНИЕ РАБОТЫ.
Установка находится в собранном состоянии. Снимают показания ртутного термометра. После проверки лаборантом установки включают нагреватель в сеть. Одновременно включают секундомер и через каждые 30 с записывают показания милливольтметра tэ и заносят результаты в таблицу. Через некоторое время металл начнет плавиться, его температура не будет изменяться до полного расплавления металла, tм – температура плавления металла.
Когда металл расплавится полностью, его температура снова будет повышаться. Продолжают нагревать жидкий металл до температуры на 40-50°С выше температуры плавления металла. Данные измерения заносят в таблицу, на основе которой строят график зависимости температуры металла от времени при нагревании. Определив температуру tэ, tэ2, tэn1, по формулам (8) находят соответствующие абсолютные температуры, и по формуле (6) находят приращение энтропии.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Как вы понимаете макросостояние и микросостояние термодинамической системы?
2. Что называется статистическим весом состояния?
3. Дайте определение энтропии.
4. Какие процессы называются обратимыми, а какие необратимыми? Приведите примеры.
5. Сформулируйте второе начало термодинамики и раскройте его статистический смысл.
6. Сделайте выводы из результатов выполнения данной работы.
ЛИТЕРАТУРА:
1. Савельев И. В. Курс общей физики, т. 1, «Наука», М., 1982, стр. 325-356.
2. Ландау Л. Д., Ахнезер А. И., Лифшиц Е. М. Курс общей физики. Механика и молекулярная физика. «Наука» ГРФМЛ М., 1965, стр. 185-194.
3. Зисман Г. А., Тодес О. М. Курс общей физики, т. 1, «Наука» ГРФМЛ М., 1969, стр. 177-194.