Лабораторная работа n 6. 02
Муромский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича и
Николая Григорьевича Столетовых»
Кафедра: «ФПМ»
Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА N 6.02
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ
ГАЗА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ
Утверждена на методическом
семинаре кафедры ФПМ
Зав.кафедрой _____________
Лабораторная работа № 6.02
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ
ГАЗА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ
Цель работы: изучение одного из возможных методов измерения Ср/Cv и определение этого отношения для воздуха.
Приборы и материалы: стеклянный баллон, манометр, поршневой насос.
ТЕХНИКА БЕЗОПАСНОСТИ
1. Осторожно обращаться с баллоном и водным манометром, не ставить их на край стола.
Согласно первому закону термодинамики количество теплоты dQ которое сообщается термодинамической системе, идёт на увеличение её внутренней энергии du и на совершение системой механической работы dA, т.е.
dQ = du + dA (1)
Элементарная работа dA есть работа расширения, равная произведению давления Р на произведение объёма dv
dA = pdv (2)
Как известно из термодинамики количество теплоты и механическая работа зависят от вида процесса. Например, для нагревания термодинамической системы на 1 К при изохорическом и изобарическом процессах надо провести ей разное количество теплоты. Величина, измеряемая количеством теплоты, необходимым для нагревания системы, называется теплоёмкостью системы С.
C = dQ/dT (3)
С учётом (1) и (2) запишем
C = dQ/dT = du/dT + pdv/dT (4)
Эта величина измеряется в джоулях на кельвин Дж/К. Теплоёмкость, отнесённая к одному молю вещества называется молярной теплоёмкостью Cm. Она измеряется в джоулях на моль-кельвин Дж/моль К. Теплоёмкость единицы массы вещества называется удельной теплоёмкостью Суд. Она измеряется Дж/кг К. Очевидно
Cm = C/m, Cуд = C/m (5)
где m - молярная масса.
Значение теплоёмкости зависит от процесса нагревания вещества. Наибольший интерес представляют теплоёмкости для случаев, когда нагревание происходит при постоянном объёмеúCmnú при постоянном давлении ÷Cmrú. В дальнейшем рассматриваем процессы в идеальном газе при измерении температуры, когда масса газа остаётся неизменной и равна 1 молю вещества. Рассмотрим изохорический процесс. Процесс называется изохорическим, если объём тела при изменении температуры остаётся постоянным, т.е. V=const. В этом случае dv=0. Следовательно, и dA=0, т.е. при этом вся подводимая к газу теплота идёт на увеличение его внутренней энергии. Тогда из уравнения (4) следует, что
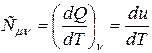 (7)
(7)
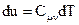 (8)
(8)
Это означает, что внутренняя энергия идеального газа зависит только от температуры. Рассмотрим изобарический процесс. Это процесс протекающий при постоянном давлении ôР = constô. Для этого случая соотношение (4) перепишется в виде:
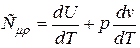 (9)
(9)
Поскольку при атмосферном давлении и комнатных температурах воздух можно с достаточно хорошим приближением считать идеальным газом, то, в этом случае можно использовать уравнение Клапейрона - Менделеева, которое для одного моля газа запишется так
PV = RT (10)
где R – универсальная газовая постоянная. Дифференцируя соотношение (10) получим PdV + VdP = RdT
Так как P = const, то dP = 0, следовательно, получаем
PdV = RdT (11)
Подставим (7) и (11) в формулу (9), получим
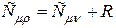 (12)
(12)
Это уравнение Майера. Оно показывает, что Сr > Cn
Это объясняется тем, что при нагревании газа при постоянном объёме всё количество теплоты идёт только на увеличение внутренней энергии газа du=CmndT, при нагревании же газа при постоянном давлении, кроме теплоты, идущей на повышение внутренней энергии газа, необходимо ещё тепло для совершения работы расширения газа PdV.
Из (11) следует, что универсальная газовая постоянная определяет работу, совершаемую одним молем газа при нагревании на 1 К при постоянном давлении. Отношение 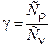 представляет собой характерную для газа величину. С учётом (12)
представляет собой характерную для газа величину. С учётом (12)
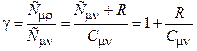 ;
; 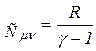 (13)
(13)
Непосредственное измерение 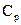 и особенно
и особенно 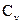 экспериментально затруднительно, так как теплоёмкость газа составит ничтожную долю теплоёмкости сосуда, заключающего газ, и поэтому измерение будет чрезвычайно ничтожно. Проще измерить отношение величин
экспериментально затруднительно, так как теплоёмкость газа составит ничтожную долю теплоёмкости сосуда, заключающего газ, и поэтому измерение будет чрезвычайно ничтожно. Проще измерить отношение величин 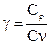
Это отношение 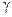 входит в уравнение Пуассона, описывающего адиабатический процесс, поэтому для определения
входит в уравнение Пуассона, описывающего адиабатический процесс, поэтому для определения 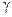 и предлагается метод адиабатического расширения. Этот процесс, протекающий без теплообмена с окружающей средой. Выведем уравнение адиабатического процесса (ур. Пуассона)
и предлагается метод адиабатического расширения. Этот процесс, протекающий без теплообмена с окружающей средой. Выведем уравнение адиабатического процесса (ур. Пуассона)
По первому началу термодинамики для адиабатического процесса имеем для одного моля газа 
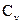 dT+PdV=0 (14)
dT+PdV=0 (14)
Из уравнения состояния идеального газа для одного моля имеем P= 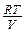
С учётом этого(14) запишется
C 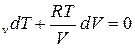
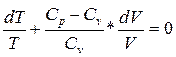
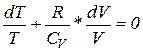
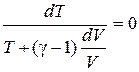
Интегрируя, а затем потенцируя полученное уравнение, найдём
TVγ-1 = const (15)
или в переменных (P,V)
PV 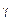 = const (16)
= const (16)
Соотношение (16) называется уравнением Пуассона. Оно описывает адиабатический процесс для идеального газа. Кривая, полученная из (16) на диаграмме (PV) называется адиабатой. Из молекулярно кинетической теории известно, что
С 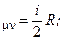 С
С 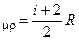 и
и 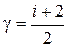 (16a)
(16a)
Здесь i число степеней свободы одной молекулы газа (для одноатомного I = 3, для двухатомного I = 5, для многоатомных газов I = 6)
ВЫПОЛНЕНИЕ РАБОТЫ
Установка для измерения состоит из стеклянного баллона А, соединённого резиновыми трубками с манометром Н. В баллоне А имеется 2 крана К1 и К2 (рис.1). Открывают кран К2. Воздух в сосуде будет иметь параметры P0; V0; T0
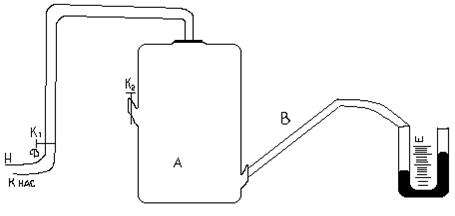
Рис. 1
P0,T0 – давление и температура окружающего воздуха. Закрывают кран К2. Открывают К1 и нагнетают в сосуд с помощью насоса Н немного воздуха. (Здесь следует иметь в виду, что при нагревании воздуха в сосуде давление в нём может возрасти настолько, что будет выброшена из манометра вода. Поэтому при нагревании воздуха в баллон разность уровней воды в коленах манометра не должна превышать 15-17 см). Температура и давление газа в сосуде несколько повысятся. Через некоторое время вследствие теплообмена с окружающей средой температура воздуха в сосуде станет равной Р0, то давление несколько понизится до Р1=Р0h1, где h1 – добавочное давление отсчитывается по манометру после прекращения теплообмена. Мысленно выделим близ крана К1 объём воздуха V и последим за изменением его параметров. После прекращения теплообмена его параметры V1; P1;T0 (рис.1). Откроем на очень короткое время кран К2, воздух в баллоне будет расширятся (причём быстро). Процесс расширения близок к адиабатическому, т.е. про быстром расширении воздух в баллоне не успевает обменяться теплом с окружающей средой. Температура газа упадёт до Т1, объём станет равным V2, а давление равным атмосферному (точка 2 рис.2). Вследствие теплообмена температура газа повысится до Т2, давление до Р2, объём останется прежним (точка 3 рис.2). Причём Р2=Р0+h2: h2 – отсчитывается по манометру. Точки 1 и 2 лежат на одной адиабате, следовательно, (Р1V1)γ = P0V2 отсюда
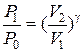
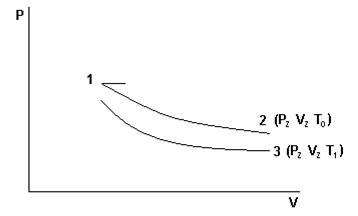
Точки 1 и 3 должны лежать на одной изотерме (T=T0=const) и можно записать P1V1=P2V2
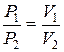 (18)
(18)
(18) возведём в степень 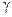
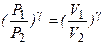
с учётом (17) получим 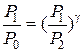
или учитывая найденные значения P1, P2
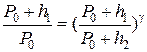 (19)
(19)
Логарифмируем (19)
Lg(P  + h
+ h  ) - lgP
) - lgP 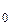 = g[lg(P
= g[lg(P 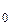 + h
+ h 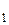 ) – lg(P
) – lg(P 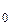 + h
+ h 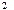 )]
)]
Отсюда g = 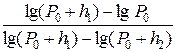
Так как давления P0, P0+h1 и P0+h2 мало отличаются друг от друга, то разность логарифмов можно принять пропорциональными разности самих давлений и приближённо принять
g = 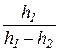
И мы получаем окончательную расчётную формулу для определения γ.
ЗАДАНИЕ К РАБОТЕ
1. Накачать в баллон воздух так, чтобы разность уровней жидкости в манометре не превышала 10-15 см. Закрыть кран К и выждать 2-4 мин, пока температура внутри баллона не станет равной температуре окружающей среды. При этом прекратится перемещение менисков в манометре. После этого отчистить показания манометра h1,отсчёт следует делать по нижнему краю мениска.
2. Быстро открыть кран К2, соединяющий баллон с атмосферой, и одновременно включить секундомер. Выдержать кран К2 открытым 5 сек. и быстро закрыть. При этом давление станет равным атмосферному, а температура понизится. Подождав 3 – 4 минуты пока температура не станет снова равной температуре окружающей среды, отсчитывают показание h2.
3. Повторяют пункты 1 и 2, выдерживая клапан открытым 5, 10, 15, 20 секунд и т. д. При этом до открытия крана К2 открывают кран К1 и, накачивая воздух в баллон(после выравнивания температуры), устанавливают тоже значение h1, что и в первом опыте. Проделывают не менее шести таких измерений. Результаты записывают в таблицу 1.
Таблица 1
| Отсчёт h1 по шкале манометра, дел | h1, дел. | τ, сек | Отсчёт h2 по шкале манометра, дел. | h2, дел. | ||
| Левый, дел. | Правый, дел. | Левый дел. | Правый дел. | |||
| 5 | ||||||
| 10 | ||||||
| 15 | ||||||
| 20 | ||||||
| 25 | ||||||
| 30 | ||||||
4. Построив график зависимости lgh2i=f(τ) определяют по графику величину h20 и определяют величину γ
5. Рассчитывают теоретическое значение коэффициента γ для воздуха по формуле (16а)
6. Рассчитывают относительную погрешность измерения 2.3 по формуле 2.4
Величина Δh20 так же, как и Δh1 может быть принята 0,5 мм. Но можно найти h20 по разносу точек на графике lgh2 = f(τ). Окончательные результаты измерений записывать в форме γ = γср ± Δγср.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Сформулируйте первое начало термодинамики и раскройте его физический смысл.
2.Дайте определение количества теплоты и внутренней энергии термодинамической системы.
3. Почему теплота и работа эквивалентны? В чём их принципиальное различие?
4. Какой процесс называется адиабатическим? Какому закону он подчиняется? Приведите пример адиабатического процесса. Постройте его график.
5. Дайте определение молярной теплоёмкости.
6. Что такое Ср и Сv? Что из них больше? Почему?
7. Вычислите Сμр и Сμν для идеального газа по молекулярно-кинетической теории.
8. Вывести уравнение Пуассона для переменных.
9. Какой процесс соответствует каждому этапу опыта(воздух накачиваем насосом, кран закрываем и т. д.)
10. Изобразите графически на диаграмме в координатах P,V процессы последовательно осуществимые в данной работе.
11. Почему перед снятием отсчётов h1 h2 нужно выжидать некоторое время?
ЛИТЕРАТУРА
1 И.В.Савельев. Курс общей физики т.1 изд. Наука 1977г. стр273-286
2.С.З Фриш, Курс общей физики т.1 гл XII §48,67
3.А.И.Китайгородский. Введение в физику. Наука 1973 стр14-153.
4.Л.П. Ландау, А.И.Ахиезер, Е.М.Лифшиц. Курс общей физики.








