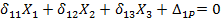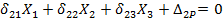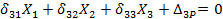Ус – ордината на эпюре (изгибающий момент от единичной силы) под центром тяжести эпюры М.

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

При вычислении перемещений строят эпюры изгибающих моментов от сил х1=1, х2=1, действующих поочередно на основную систему по направлению соответствующих лишних неизвестных.

 

 

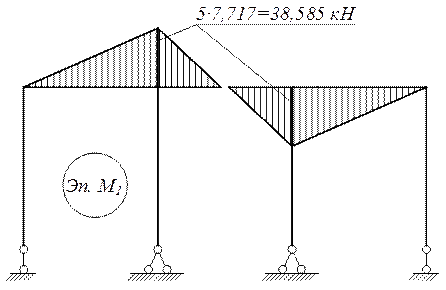
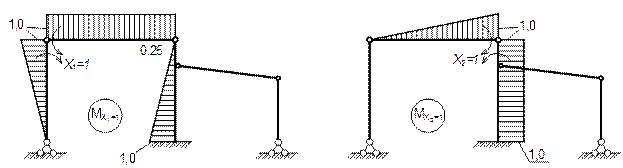
Эпюра М от единичной силы х1=1

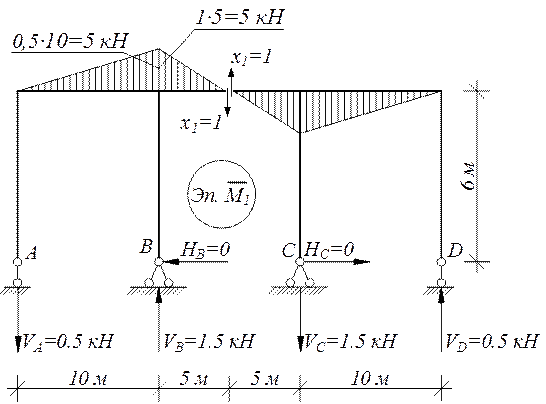
ΣMB=-VA∙10+1∙5=0; VA=0,5 kH;

ΣMA=-VB∙10+1∙15=0; VB=1,5 kH.

 

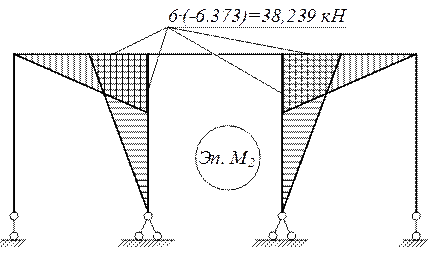
Эпюра М от единичной силы х2=1

 

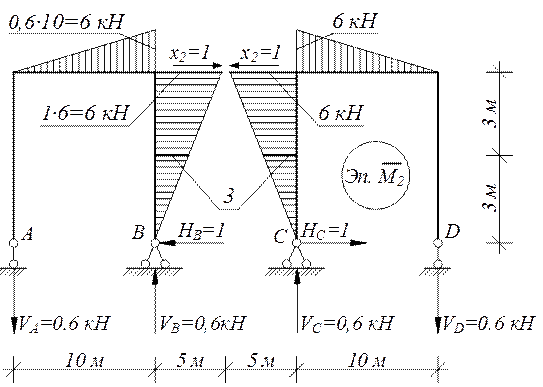
ΣMB=-VA∙10+1∙6=0; VA=0,6 kH;

ΣMA=-VB∙10+1∙6=0; VB=0,6 kH.

 

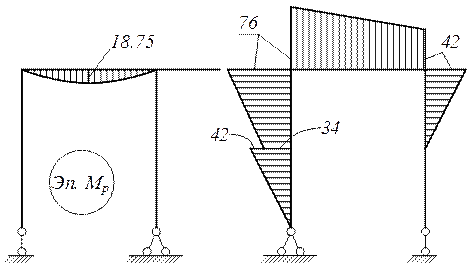
Грузовая эпюра М от заданной нагрузки

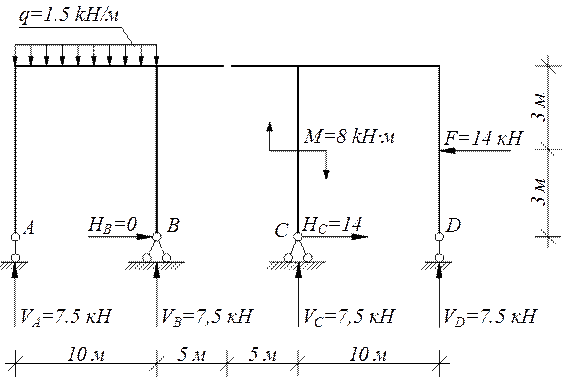
ΣMD =-14∙3+8+ VC ∙10=0; VC =3,4 kH ;

ΣME =8+3,4∙10- HC ∙3=0; HC =14 kH ;

ΣMC = VD ∙10+8+14∙3=0; VD =3,4 kH .

 

Грузовая эпюра Мр изгибающих моментов от заданной нагрузки в основной системе

 

 

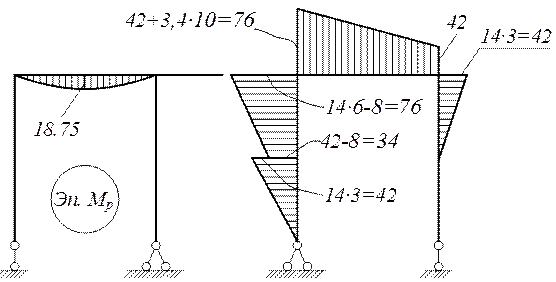
Все эпюры строятся на растянутых волокнах стержней рамы.

 

 

Перемножением единичных эпюр вычисляют все коэффициенты при неизвестных системы канонических уравнений.

 

Например, единичное перемещение 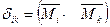вычисляют умножением единичной эпюры 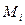на единичную эпюру .

 

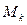Перемножением единичных эпюр 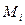с грузовой 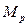вычислят все возможные или грузовые члены:

 

 

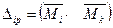
При перемножении эпюр необходимо соблюдать следующие условия:

1. Одна из эпюр должна быть прямолинейной.

2. Ордината Ус в выражении 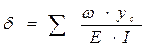должна быть взята с прямолинейной эпюры.

3. Если обе эпюры прямолинейны, то ордината Ус под центром тяжести можно брать из любой эпюры.

4. Произведение положительно, если обе эпюры одного знака, т.е. эпюры отложены с одной стороны стержня.

Если перемножаемые эпюры разных знаков, то произведение, а следовательно и перемещение – отрицательны.

 

Определяем коэффициенты канонических уравнений по правилу Верещагина:

 

 

 

 

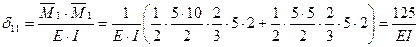
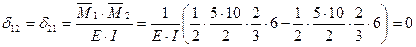
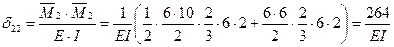
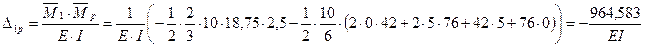
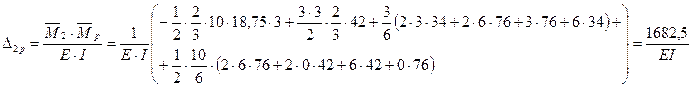
Для проверки правильности коэффициентов канонических уравнений строим суммарную единичную эпюру М.

 

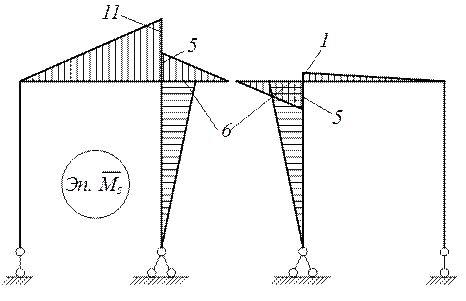
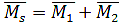
Универсальная проверка:

 

 

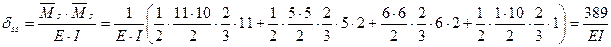
С другой стороны:

 

 

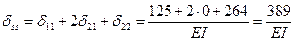
Постолбцовая проверка:

 

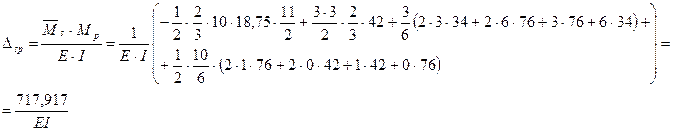
С другой стороны:

 

 

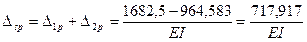
Подставляя найденные коэффициенты в канонические уравнения, определяем х1 и х2:

 

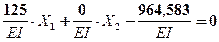X1=7,717 kH

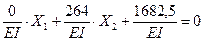X2=-6,373 kH

Поскольку рама симметрична, то изначально можно было использовать систему канонических уравнений вида

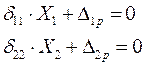
Строим исправленные эпюры моментов.

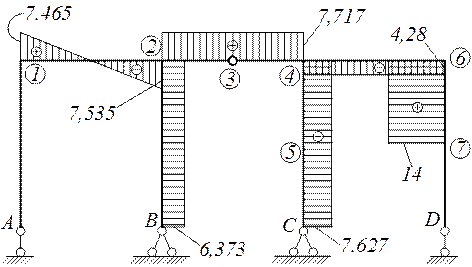
Окончательная эп. М ( M = M 1 + M 2 + Mp)

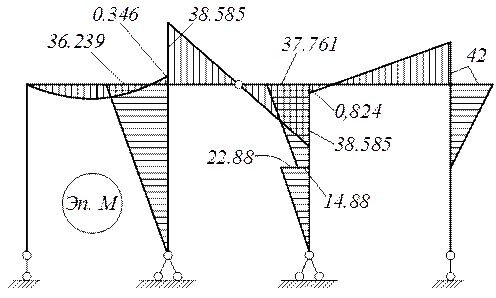
Проверка окончательной эпюры

 

 

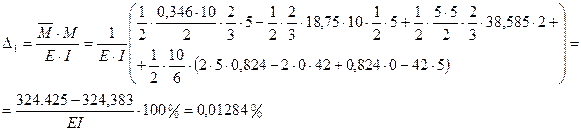
Окончательная эпюра построена верно.

 

 

Построение эпюр поперечных сил Q .

Эпюру Q строим по эпюре М, используя зависимость

 

 

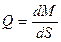
Иными словами, величина поперечной силы равна тангенсу угла наклона касательной к эпюре М в рассматриваемом сечении. Если для этого ось нужно повернуть на острый угол по часовой стрелке, то величина Q на этом участке положительна.

 

 

Q=dM/dx

 

 

 

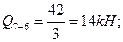
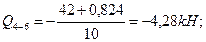
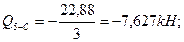
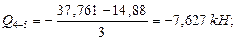
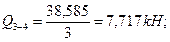
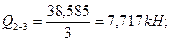
Q1-2=? Q1=? Q2=?

 

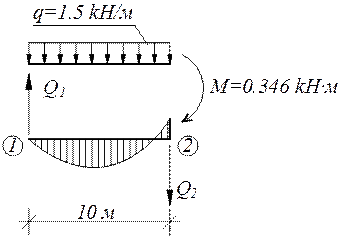
Q 2 =?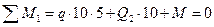

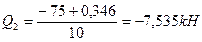
Q 1 =?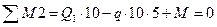

 

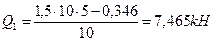
По полученным значениям строим эпюру Q.

 

По эпюре Q строим эпюру N.

 

При этом Q>0 вращает вырезанный узел по часовой стрелке.

 

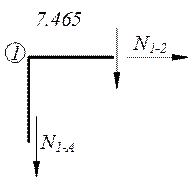
Σ Y=-7,465-N1-A=0; N1-A=-7,465kH

Σ X=N1-2=0; N1-2=0

 

 

 

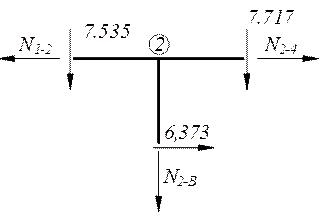
Σ Y=-7,535-7,717 – N2-B=0;

NEB= - 15,252 kH

Σ X=N2-4+6,373=0;

N2-4= - 6,373 kH

 

Σ X=NEF=0; NEF=0

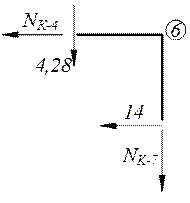
Σ Y= - 4,28 - NK-7=0; NK-7= - 4,28 kH

Σ X=-NK-4 - 14=0; NK-4= - 14 kH

 

 

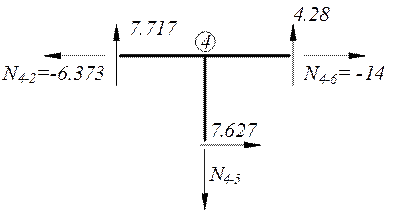
Σ Y = 7,717+4,28- N 4-5 =0;

N 4-5 = 11,997 kH

Σ X =6,373+7,627+14=0

 

Строим эпюру N по полученным данным

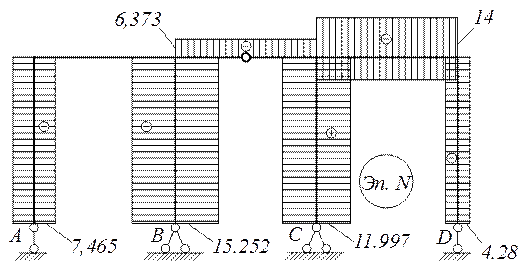
Проверка равновесия рамы

 

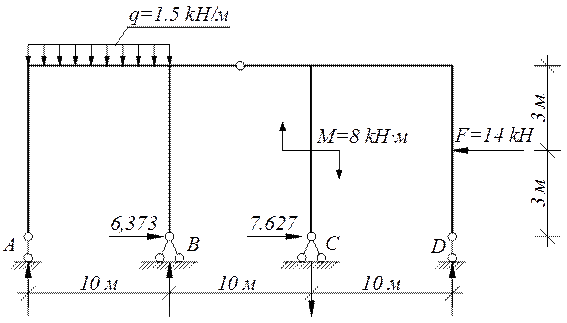
ΣX=6,373+7,627-14=0

Σ Y =-1,5∙10+7,465+15,272= - 11.997 + 4.28 = 0

Σ ME =(1.5∙102)/2 +8+14∙3-6,373∙6-7,627∙6-15,252∙10+11,997∙20-4,28∙30=0

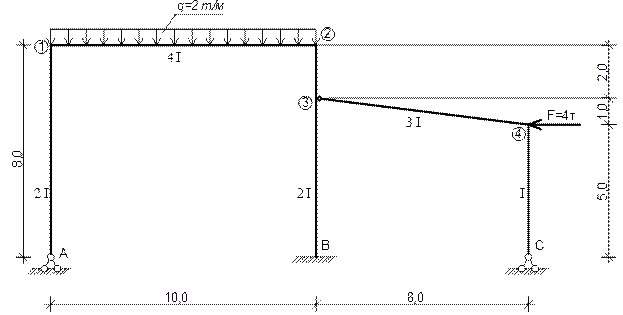
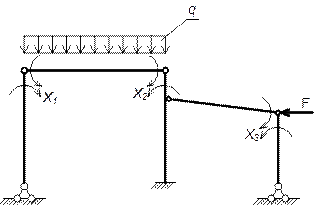
ПРИМЕР РАСЧЁТА ПЛОСКОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ СИЛ РАСЧЁТНАЯ СХЕМА

1. СТЕПЕНЬ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ РАМЫ РАВНА КОЛИЧЕСТВУ «ЛИШНИХ» СВЯЗЕЙ:

ССН=Соп + 3К – I -3 = 7 +3 ∙0 – 1 – 3 =3, где:

Соп - число опорных стержней;

Ш – приведенное число простых шарниров, связывающие диски между

собой;

3 – три статических условия равновесия

К – число замкнутых контуров.

 

2. ВЫБОР ОСНОВНОЙ СИСТЕМЫ.

Построение основных эпюр изгибающих моментов.

Основная система образуется из заданной рамы путём отбрасывания «лишних» связей и замены их силами, реакциями отброшенных связей, которые принимаются за основные неизвестные.

Рассмотрим несколько вариантов основной системы.

I вариант

 

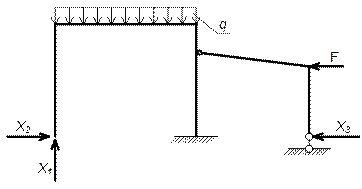
Основные эпюры

 

 

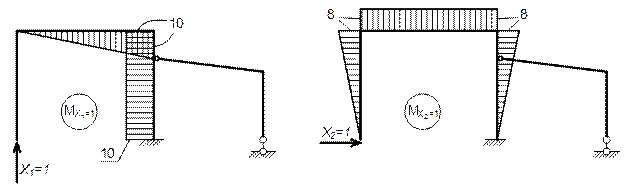
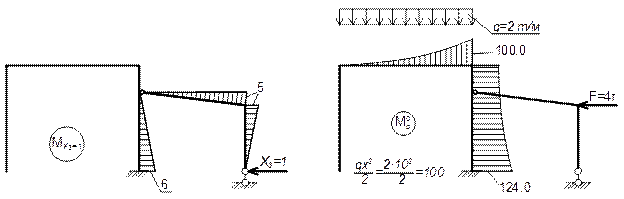
II вариант

Основные эпюры

 

 

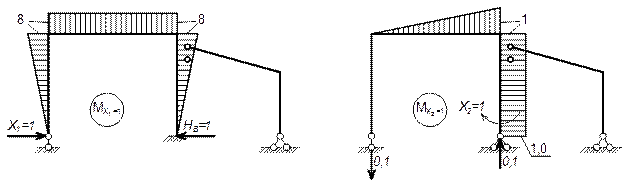
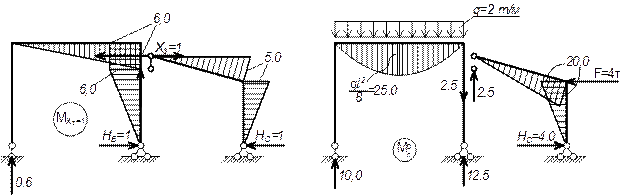
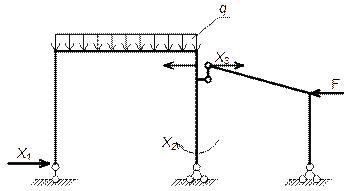
III вариант

Основные эпюры

 

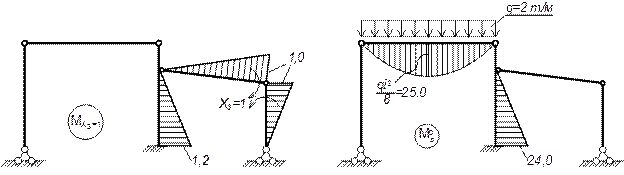
Рекомендуется самостоятельно рассмотреть и другие возможные вариант основной системы.

Анализируя приведенные варианты, приходим я выводу, что 3 вариант обеспечивают меньшую трудоемкость при вычислении перемещений и 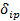(см.п.4) и большую надёжность при определении основных неизвестных [4, $61].

 

3. Принимаем для дальнейшего расчёта 3 варианта основной системы как более рациональной.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ