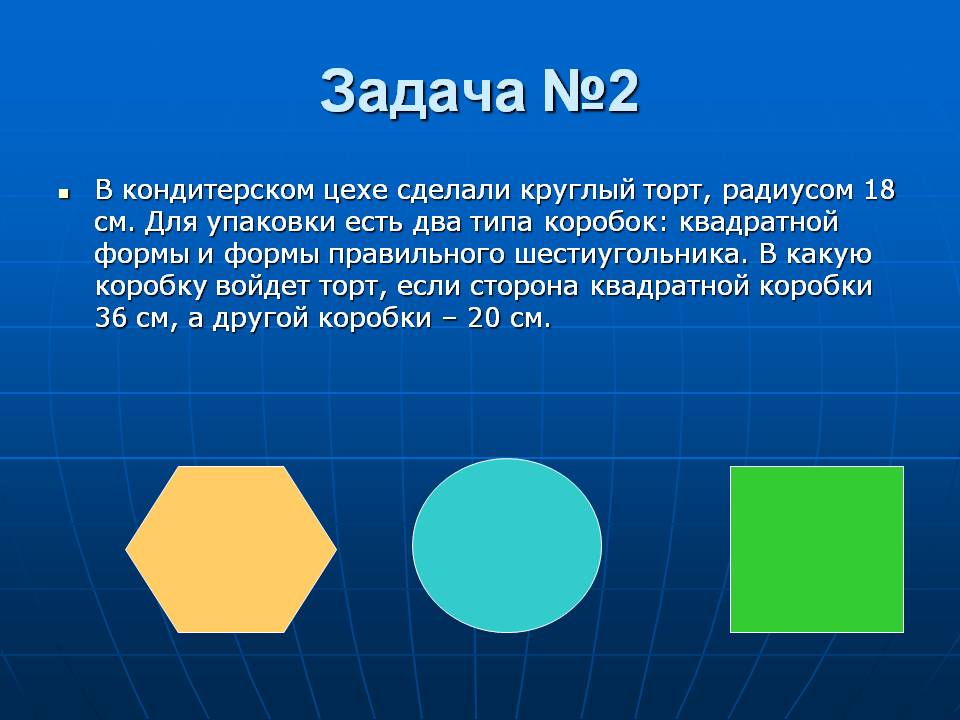
Правильный треугольник

Дата: 2025-06-14; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Обобщим информацию о правильном (равностороннем) треугольнике.
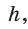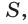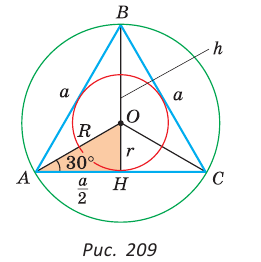
Запишем формулы высоты площади радиуса R описанной и радиуса 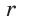вписанной окружностей правильного треугольника АВС со стороной 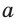(рис. 209):

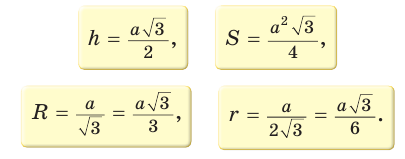
Из 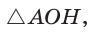где 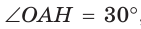, следует, что

При заданной стороне 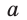правильного треугольника его можно построить при помощи циркуля и линейки, используя алгоритм построения треугольника по трем сторонам.

Так как Для построения описанной и вписанной оружностей правильного треугольника достаточно по- строить его медианы (высоты), точка пересечения которых будет центром искомых окружностей.

Правильный четырехугольник

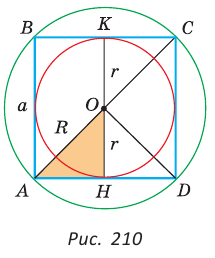
Пусть сторона квадрата ABCD равна 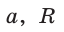— ра­диус описанной, 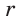— радиус вписанной окружности (рис. 210). Диаметр его описанной окружности ра­вен диагонали АС. В свою очередь, 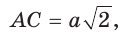откуда 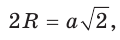или 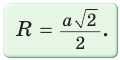Из равнобедренного прямоугольного треугольника также следует, что
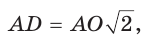
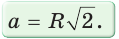
Диаметр КН окружности, вписанной в квадрат, равен длине стороны квадрата, т. е. КН = АВ = а, откуда 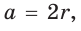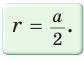[ Из прямоугольного равнобедренного треугольника АОН также следует,
что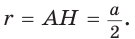

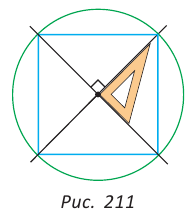
Для построения квадрата, вписанного в данную окружность с заданным центром, можно построить две взаимно перпендикулярные прямые, проходящие че­рез центр окружности (рис. 211). Эти прямые пересекут окружность в вершинах квадрата. Обоснуйте это утверждение. Выполните указанное построение при помощи чертежного треугольника.

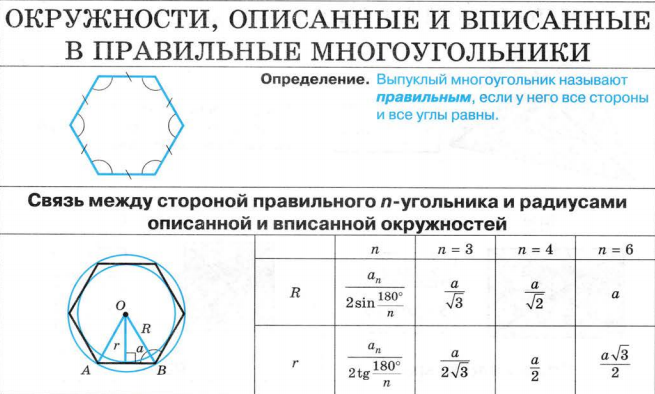
Правильный шестиугольник

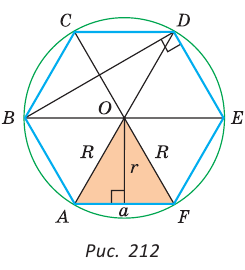
Рассмотрим правильный 6-угольник ABCDEF со стороной 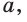вписанный в окружность с центром О и радиусом R (рис. 212). Его внутренние углы равны по 120°. Треугольник AOF равнобедренный,
так как ОА = OF = R, 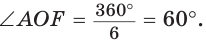Поэтому 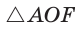— равносторонний, откуда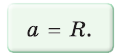

Так как радиус 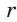вписанной окружности является высотой равностороннего треугольника со сто­роной а, то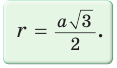

Поскольку 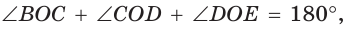то большая (главная) диаго­наль BE правильного шестиугольника проходит через его центр О, а все три большие диагонали AD, BE и CF разбивают его на шесть равных равносторонних треугольников. Площадь правильного шестиугольника

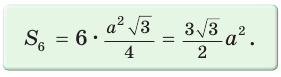
Меньшая (малая) диагональ BD правильного шестиугольника является диагональю ромба BCDO (ВС = CD = DO = ВО - а) с углами, равными 60° и 120°. Откуда 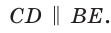Треугольник BDE является прямоугольным ( 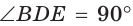как опирающийся на диаметр),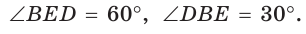
Кроме того, 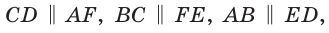а расстояния между указанными парами параллельных прямых равны 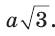Докажите это самостоятельно.
Построим при помощи циркуля и линейки правильный шестиугольник, вписанный в данную окружность с радиусом R(рис. 213, а). Воспользуемся тем, что а = R, где а — сторона правильного шестиугольника.

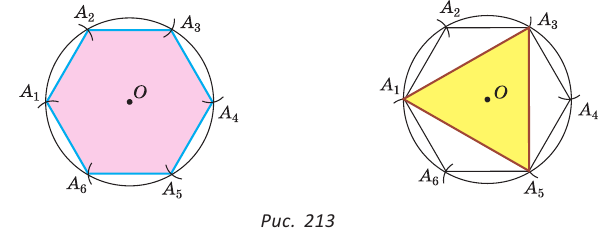
Одну вершину 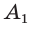шестиугольника берем на окружности произвольно. Из нее как из центра радиусом, равным радиусу R, делаем засечку на окружности и получаем вершину 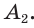Затем аналогично последовательно строим остальные вершины: 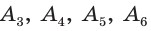— и соединяем их отрезками. Из равенства равносторонних треугольников (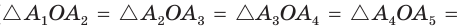

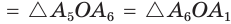) следует равенство углов построенного шестиугольника 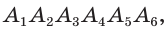откуда заключаем, что он — правильный.
Для построения правильного треугольника, вписанного в данную окружность, достаточно соединить отрезками через одну вершины правильного вписанного шестиугольника (рис. 213, б). Для построения правильного 12-угольника следует разделить дуги 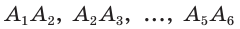пополам (построив серединные перпендикуляры к сторонам правильного шести­угольника) и каждую из точек деления соединить отрезками с концами соответствующей стороны.
Применяя указанный способ деления дуг пополам, можно с помощью циркуля и линейки построить множество правильных многоугольников.
Так, из правильного 4-угольника можно построить правильный 8-угольник, 16-угольник, и вообще любой правильный 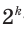-угольник, где 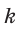— целое число, большее двух.

Пример №9

В окружности с центром О проведен диаметр BD, через середину радиуса OD проведена хорда АС, перпендикулярная диаметру BD (рис. 214). Доказать, что 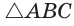— правильный.

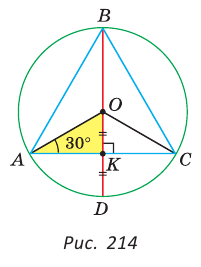
Доказательство:

Так как 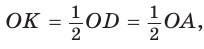то в прямоугольном треугольнике 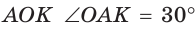. В равнобедренном треугольнике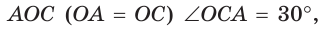 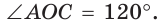Вписанный угол АВС равен половине центрального угла АОС, т. е. 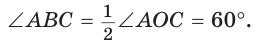Диаметр, перпендикулярный хорде, делит ее пополам.
Поэтому АК = КС. Так как в треугольнике АВС высо­та ВК является и медианой, то он — равнобедренный, АВ = ВС. Отсюда 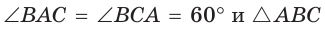— равно­сторонний, т. е. правильный. Что и требовалось доказать.
Замечание. Из задачи следует второй способ построения правильного треугольника, вписанного в окружность: строится диаметр BD, через середину радиуса OD проводится хорда АС, перпендикулярная диаметру. Треугольник АВС — правильный.

Пример №10

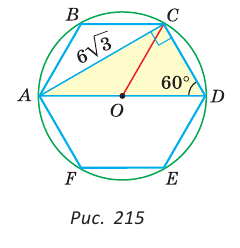
Дан правильный шестиугольник ABCDEF, диагональ АС равна 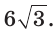Найти площадь шестиугольника (рис. 215).

Решение:

Вписанный угол ACD опирается на диаметр А D, поэтому он прямой. Из прямоугольного треугольника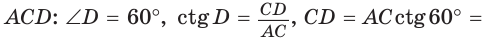


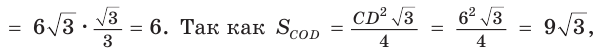
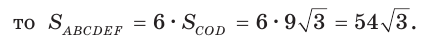
Ответ: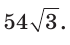

Пример №16

Существует ли правильный многоугольник, угол которого равен: 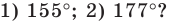В случае утвердительного ответа укажите вид многоугольника.

Решение:

1) Пусть 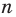— количество сторон искомого правильного многоугольника. С одной стороны, сумма его углов равна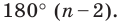

С другой стороны, эта сумма равна 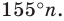Следовательно,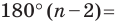 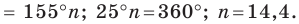Поскольку 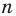должно быть натуральным числом, то такого правильного многоугольника не существует.

2) Имеем: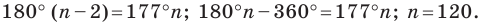

Ответ: 1) не существует; 2) существует, это — стодвадцатиугольник.

Пример №17

В окружность вписан правильный треугольник со стороной 18 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

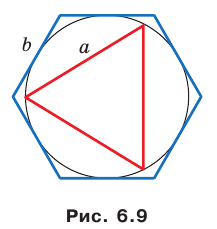
Решение:

Радиус окружности, описанной около правильного треугольника, вычисляют по формул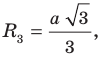е где 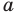— длина стороны треугольника (рис. 6.9). Следовательно,

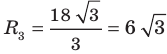(см)

По условию радиус окружности, вписанной в правильный шестиугольник, равен радиусу окружности, описанной около правильного треугольника, то есть 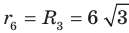см. Поскольку 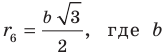— длина стороны правильного шестиугольника, то

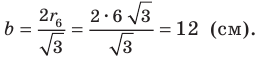
Ответ: 12 см.

Письменное задание:

1)Записать теорию

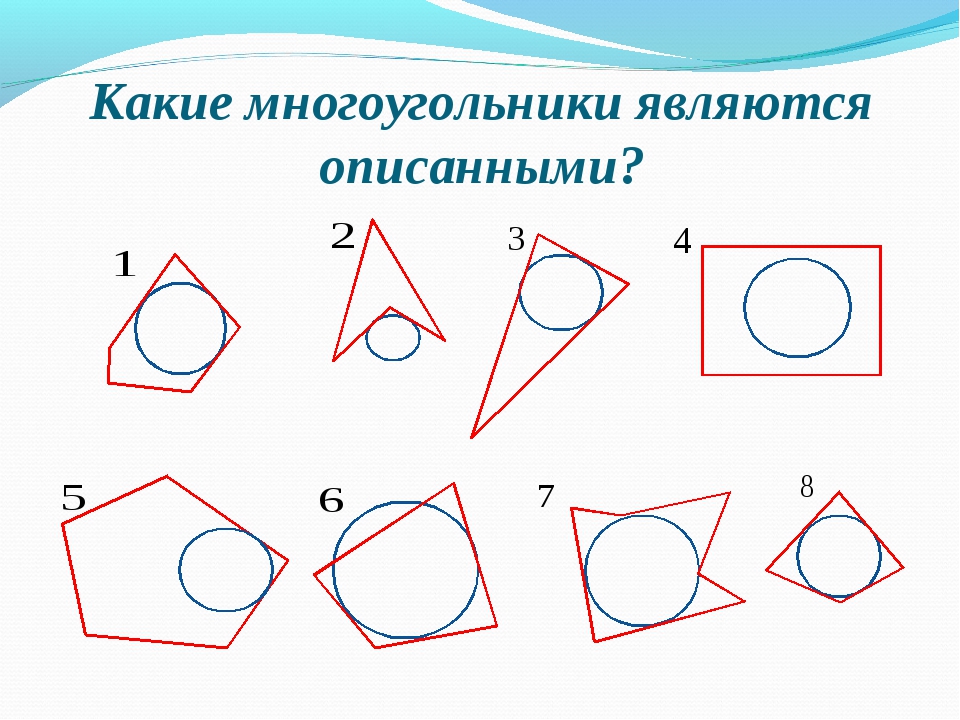
2)Ответить на вопрос: (записать номера фигур без рисунка)

3)Записать решение примера №16(документ).

Домашнее задание: решить задачу