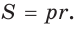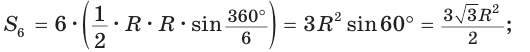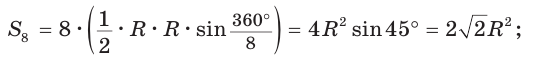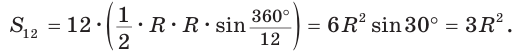Правильные многоугольники с примерами

Дата: 2025-06-14; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны и все углы равны.


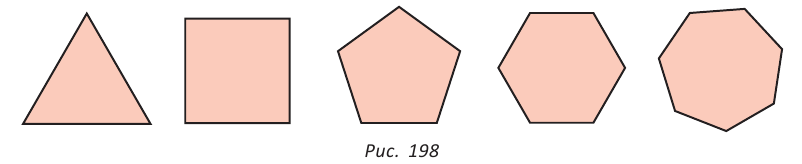
На рисунке 198 изображены правильные треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник. Правильный треуголь­ник — это равносторонний треугольник, а правильный четырехугольник — это квадрат.

Одной из простейших задач является задача нахождения величины внутреннего угла правильного многоугольника. Так как все углы правильного 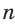-угольника равны между собой, а сумма углов любого 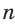-угольника равна 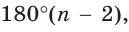то угол 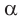правильного 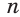-угольника можно найти по формуле

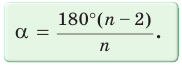
Например, для правильного шестиугольника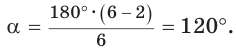

Теорема. Около любого правильного многоугольника можно описать окружность, в любой правильный многоугольник можно вписать окружность; центры этих окружностей совпадают.

Доказательство:

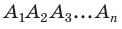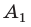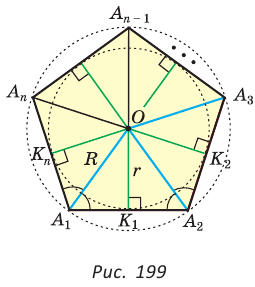
В правильном многоугольнике проведем биссектрисы внутренних углов и 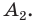Пусть О — точка пересечения этих биссектрис (рис. 199). Так как 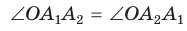как половины равных углов, то 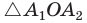— равнобедренный с основанием 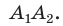Проведя отрезок 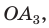получим 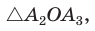равный 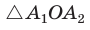по двум сторонам и углу между ними ( 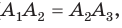сторона 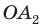— общая, ).

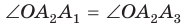Соединив точку О отрезками с остальными вершинами, получим множество равных равнобедренных треугольников. Отсюда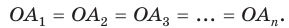

Поэтому окружность с центром О и радиусом 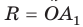пройдет через все вершины многоугольника 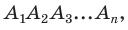т. е. будет его описанной окружностью.

А поскольку высоты указанных равных равнобедренных треугольников, проведенные к их основаниям, равны, т. е. 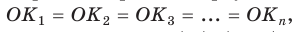то точка О — также и центр вписанной окружности многоугольника 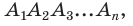радиус которой 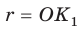. Теорема доказана.

Точка О называется центром правильного 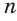-угольника.

Формулы радиусов описанной и вписанной окружностей правильного многоугольника

Пусть 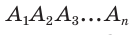— правильный 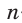-угольник со стороной 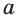, где О— его центр, 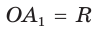— радиус описанной окружности, 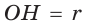— радиус вписанной окружности (рис. 202).

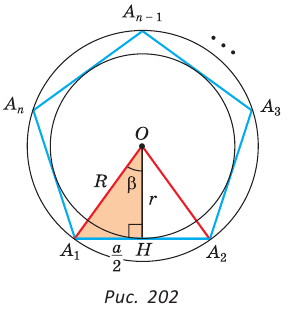
Так как 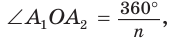а высота ОН равнобедренного треугольника 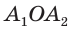является биссектрисой и медианой, то угол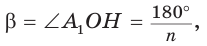 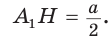Из прямоугольного треугольника 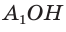находим:

а) 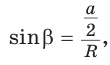откуда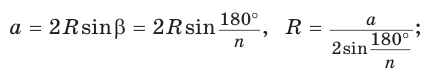

б) 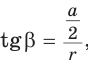откуда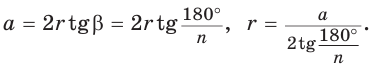

Замечание. Выведенные формулы запоминать не обязательно. Важно помнить способ их получения: решение прямоугольного треугольника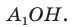

Примеры:

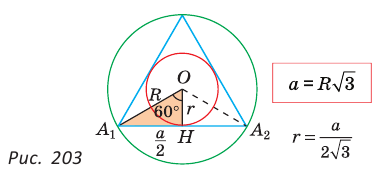
1) Для правильного треугольника (рис. 203) получим:

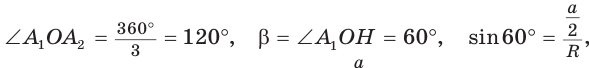откуда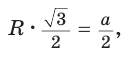

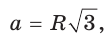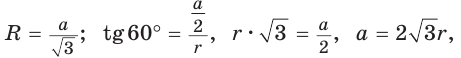или или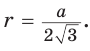

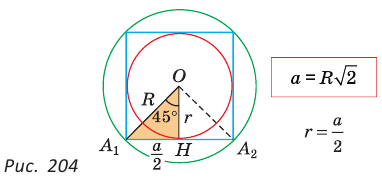
2) Для правильного четырехугольника (рис. 204) получим:

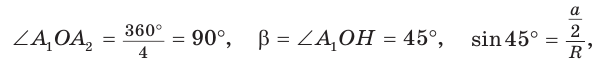откуда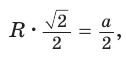

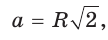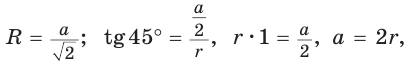или или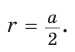

3) Для правильного шестиугольника (рис. 205)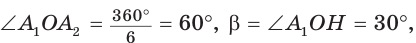

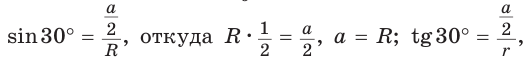
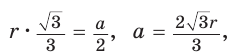или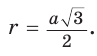

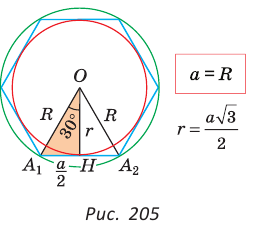
Полезно запомнить формулы, выражающие сторону 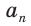правильного 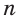-угольника через радиус R описанной окружности при 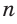= 3, 4, 6:

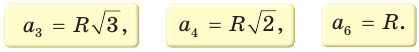
Для нахождения площади правильного 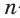-угольника 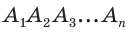с центром О и радиусом R описанной окружности можно найти площадь треугольника 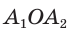по формуле 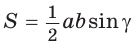и умножить ее на число таких треугольников, т. е. на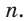

Пример:

Для нахождения радиуса 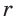окружности, вписанной в правильный мно­гоугольник, можно использовать формулу площади описанного многоугольника