Окружность, вписанная в правильный многоугольник
Известно, что в любой правильный треугольник можно вписать окружность. Рассмотрим вопрос о существовании окружности, вписанной в правильный многоугольник.
Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности. При этом многоугольник называется описанным около окружности.
Докажем, что в любой правильный многоугольник можно вписать окружность.
Теорема 2 (об окружности, вписанной в правильный многоугольник). В любой правильный многоугольник можно вписать единственную окружность.
I. Докажем существование окружности.
1) Пусть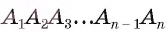 
— правильный многоугольник. Докажем, что существует точка, равноудаленная от прямых, содержащих стороны многоугольника (рис. 84).
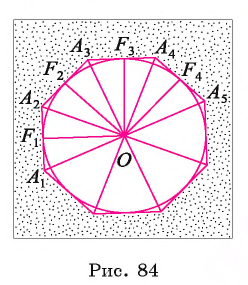
2) Пусть точка О — центр описанной около многоугольника окружности. Теперь проведем высоты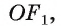 
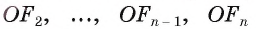соответственно треугольников 
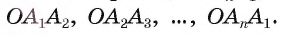Как было доказано в предыдущей теореме, эти треугольники равны между собой, следовательно, равны их высоты, т. е.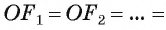 
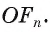
3) Таким образом, окружность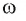 
с центром в точке О радиуса 
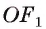проходит через точки 
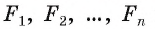и касается сторон многоугольника в этих точках, т. е. эта окружность вписана в правильный многоугольник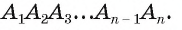 
Заметим также, что центр О вписанной в правильный многоугольник окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Подчеркнем, что для правильного многоугольника центр вписанной окружности совпадает с центром, описанной окружности.
II. Докажем, что вписанная окружность единственная.
Предположим, что существует еще одна окружность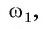 
вписанная в правильный многоугольник 
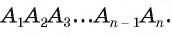Тогда центр Ох этой окружности равноудален от сторон многоугольника, т. е. точка О, лежит на каждой из биссектрис углов многоугольника, а значит, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. он равен 
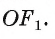Следовательно, окружности 
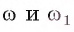совпадают.
Теорема доказана.
Центром, правильного многоугольника называется центр его вписанной и описанной окружностей.
Выражение элементов n-угольника через радиус вписанной или описанной окружностей
Пусть S — площадь правильного n-угольника,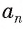 
— длина его стороны, Р — периметр, а г и R — радиусы вписанной и описанной окружностей соответственно.
1) Площадь S правильного n-уголъника, описанного около окружности, можно найти, зная периметр Р и радиус г вписанной окружности, по формуле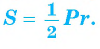 
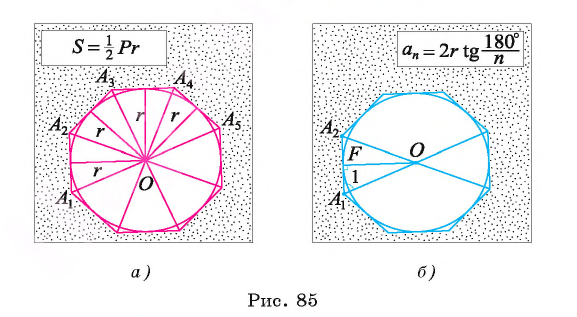
Соединим центр О правильного многоугольника с его вершинами (рис. 85, а). Тогда многоугольник разбивается на n равных треугольников, площадь каждого из которых равна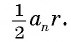 
Следовательно,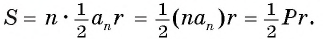 
Что и требовалось доказать.
2) Длину стороны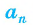 
правильного n-угольника можно найти, зная радиус г вписанной окружности, по формуле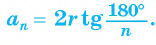 
Соединим центр многоугольника с вершинами 
и проведем высоту OF равнобедренного треугольника 
(рис. 85, б). Так как многоугольник правильный, то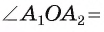 
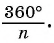в равнобедренном треугольнике 
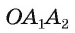высота OF, проведенная к основанию, является биссектрисой, следовательно, 
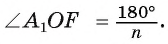Таким образом,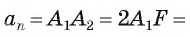 
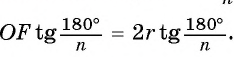
Что и требовалось доказать.
Так как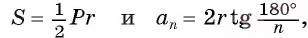 
, то площадь S =
3) Длину стороны аn правильного n-угольника можно найти, зная радиус R описанной окружности, по формуле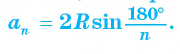 
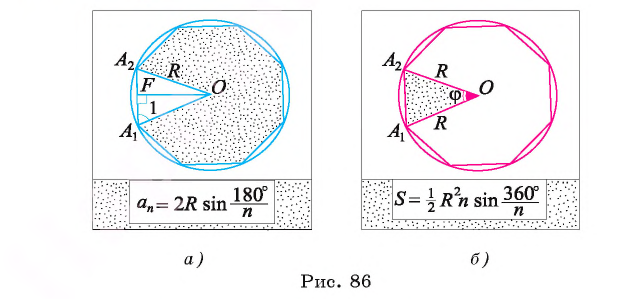
Пусть OF — высота равнобедренного треугольника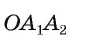 
(рис. 86, а). Тогда 
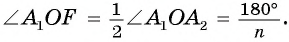В прямоугольном треугольнике 
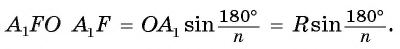Таким образом,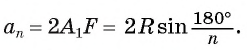 
Что и требовалось доказать.
Для правильного треугольника (n = 3), квадрата (n = 4) и правильного шестиугольника, (n = 6) получим соответственно формулы: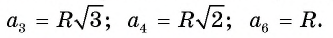 
4) Площадь S правильного п-угольника можно найти, зная радиус R описанной окружности, по формуле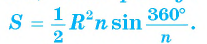 
Соединим вершины правильного /i-угольника с его центром (рис 86, б). Тогда многоугольник разобьется на п равных треугольников. Следовательно,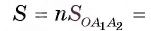 
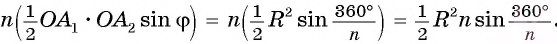
Что и требовалось доказать.
5) Радиус г вписанной окружности можно найти, зная радиус R описанной окружности, по формуле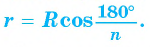 
В прямоугольном треугольнике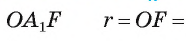 
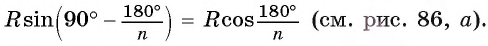
Что и требовалось доказать.
Построение правильных многоугольников
Вопрос о построении правильного треугольника уже рассматривался ранее. Покажем, каким образом можно с помощью циркуля и линейки построить правильный треугольник, вписанный в окружность.
Пример №1
Постройте правильный треугольник, вписанный в данную окружность.
Поиск решения.
Пусть правильный треугольник ABC вписан в окружность с центром в точке О. Проведем диаметр BF этой окружности, обозначим буквой Т точку пересечения этого диаметра со стороной АС. Тогда положение точки Т на отрезке OF характеризуется равенством ОТ = TF; т. к. центр равностороннего треугольника есть точка пересечения медиан, то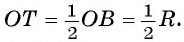 
Кроме того, 
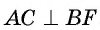Теперь можем осуществить построение (рис. 87, а).
Построение.
1) Проводим диаметр BF окружности и строим точку Т — середину отрезка OF (рис. 87, б).
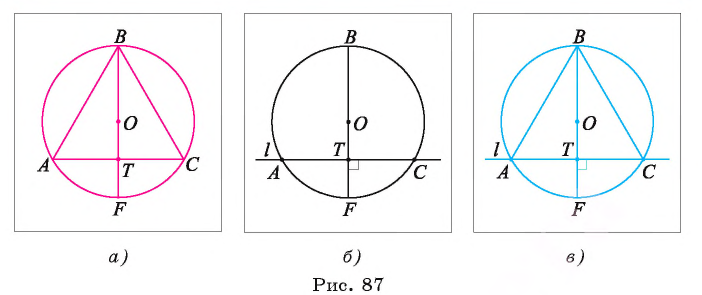
Строим прямую l, которая проходит через точку Т и перпендикулярна диаметру BF (рис. 87, б).
3) Отметим точки А и С пересечения прямой l с окружностью.
4) Строим отрезки ВА и ВС (рис. 87, в). Треугольник ABC — искомый.
Докажите самостоятельно, что построенный треугольник — правильный.
Пример №2
Постройте правильный шестиугольник, сторона которого равна данному отрезку а.
Поиск решения.
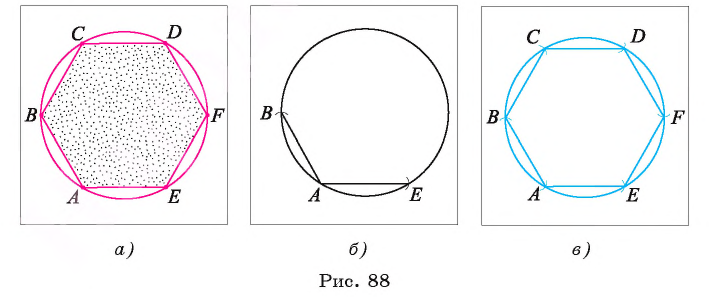
Пусть ABCDFE — правильный шестиугольник, сторона. которого равна а. Рассмотрим, описанную около этого шестиугольника окружность. Известно, что радиус окружности, описанной около правильного шестиугольника, равен его стороне, т. е. R = АВ = ВС = CD = DF = FE = ЕА = a.(рис. 88). Этим можем воспользоваться для построения шестиугольника.
Построение.
1) Строим окружность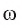 
с центром О и радиуса а.
2) Выбираем на этой окружности произвольную точку А и строим окружность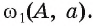 
Отметим точки В и Е пересечения окружности 
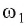, с окружностью 
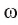(рис. 88, б).
3) Далее строим точку С, которая является одной из точек пересечения окружности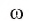 
и окружности 
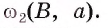Аналогично строим точки D и F. Шестиугольник ABCDFE — искомый (рис. 88, в).
Заметим, что результат задачи 1 позволяет построить правильный шестиугольник, если построен правильный треугольник.