Определение правильного многоугольника
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
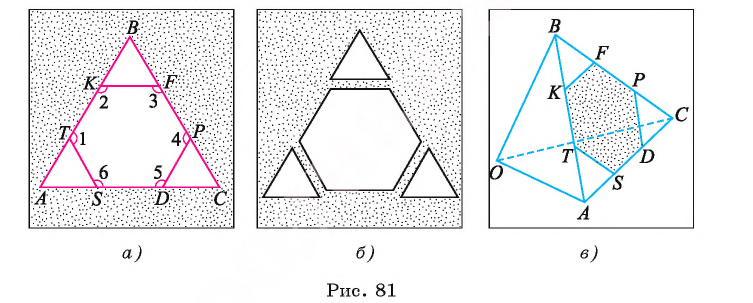
Рассмотрим пример. Пусть ABC — равносторонний треугольник;. Разделим каждую его сторону на три равные части, как показано на рисунке 81, а. Каждый из треугольников ATS, KBF и DPC является равносторонним. Отсюда следует, что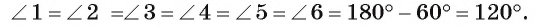 
Модель этого правильного многоугольника получится, если от листа бумаги, имеющего форму равностороннего треугольника, отрезать равные части, имеющие форму равносторонних и равных между собой треугольников, как показано на рисунке 81, б.
Если треугольник АБС является гранью тетраэдра ВОАС (тетраэдр — треугольная пирамида, у которой все четыре грани — равные равносторонние треугольники), а каждая пара точек Т, К, F, Р и D, S делит соответственно ребра АВ, ВС и АС на три равные части, то TKFPDS — правильный шестиугольник, лежащий на грани ABC (рис. 81, в).
Ранее, в § 1 главы 1 учебного пособия «Геометрия, 8», была доказана теорема о том, что сумма градусных мер углов любого выпуклого n-угольника равна 180°(n - 2). Из доказанной теоремы и определения правильного n-угольника следует, что градусную меру каждого его угла можно найти по формуле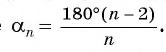 
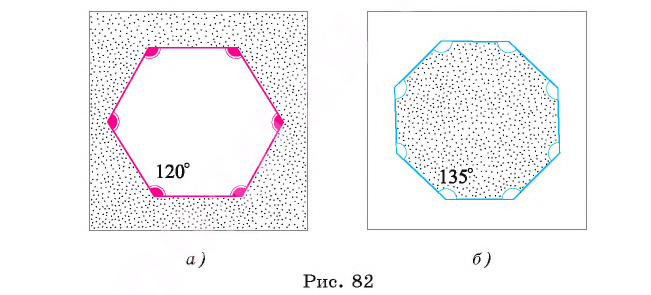
Например, для правильного шести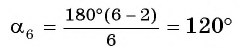 
(рис. 82, о), а для правильного восьмиугольника 
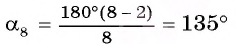(рис. 82, б).
Окружность, описанная около правильного многоугольника
Вы знаете, что около правильного треугольника и правильного четырехугольника можно описать окружность. Теперь изучим вопрос о существовании окружности, описанной около правильного многоугольника.
Определение. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. При этом многоугольник называется вписанным в окружность.
Оказывается, что около любого правильного многоугольника можно описать окружность. Докажем следующую теорему.
Теорема 1 (об окружности, описанной около правильного многоугольника). Около любого правильного многоугольника можно описать единственную окружность.
Доказательство.
I. Докажем, существование окружности.
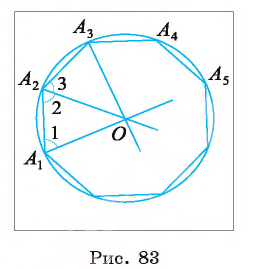
1) Пусть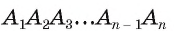 
— правильный многоугольник. Докажем, что существует точка, равноудаленная от всех его вершин. Пусть точка О — точка пересечения биссектрис углов 
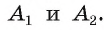Соединим точку О отрезками со всеми вершинами многоугольника и докажем, что 
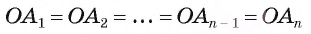(рис. 83).
2) Так как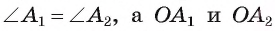 
— биссектрисы, то 
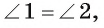т. е. треугольник 
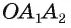— равнобедренный, а значит,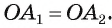 
3) Заметим, что треугольник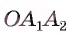 
равен треугольнику 
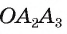по двум сторонам и углу между ними ( 
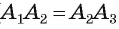,сторона 
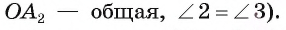. Из равенства этих треугольников следует, что 
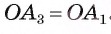Так же можно доказать, что 
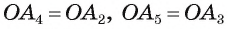и т. д.
4) Таким образом,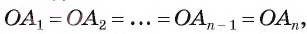 
т. е. точка О равноудалена от вершин многоугольника. Следовательно, окружность со с центром в точке О и радиуса ОА, является описанной около многоугольника. Из доказательства следует, что центром, окружности, описанной около правильного многоугольника, является точка пересечения биссектрис углов этого многоугольника.
II. Докажем, что описанная окружность единственная.
Пусть существует еще одна окружность со,, которая описана около правильного многоугольника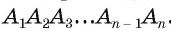 
Тогда эта окружность является описанной, например, около треугольника 
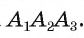Но около треугольника 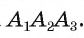можно описать единственную окружность, значит, окружности со и со, совпадают, т. е. около многоугольника 
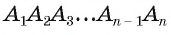можно описать единственную окружность.
Теорема доказана.