Функции нескольких переменных
Функция 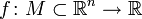 переменных
переменных 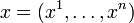 является дифференцируемой в точке
является дифференцируемой в точке 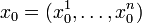 своей области определения
своей области определения 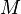 , если для любой точки
, если для любой точки 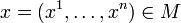 существуют такие константы
существуют такие константы 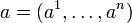 , что
, что
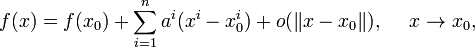 где
где 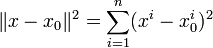 .В этой записи функция
.В этой записи функция 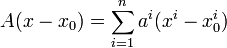
является дифференциалом функции 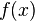 в точке
в точке 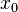 , а числа
, а числа 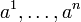 являются частными производными функции
являются частными производными функции 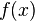 в точке
в точке 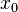 , то есть
, то есть
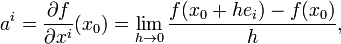 где
где 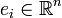 — вектор, все компоненты которого, кроме
— вектор, все компоненты которого, кроме 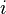 -ой, равны нулю, а
-ой, равны нулю, а 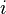 -ая компонента равна 1.
-ая компонента равна 1.
Каждая дифференцируемая в точке функция имеет в этой точке все частные производные, но не каждая функция, имеющая все частные производные, является дифференцируемой. Более того, существование частных производных в некоторой точке не гарантирует даже непрерывность функции в этой точке. В качестве такого примера можно рассмотреть функцию двух переменных 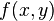 , равную
, равную 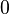 при
при 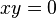 и
и 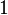 при
при 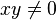 . В начале координат обе частные производные существуют (равны нулю), но функция не является непрерывной.
. В начале координат обе частные производные существуют (равны нулю), но функция не является непрерывной.
Это обстоятельство могло бы стать серьезной помехой всему дифференциальному исчислению функций многих переменных, если бы не выяснилось, что непрерывности частных производных в точке достаточно для дифференцируемости функции в этой точке.[1]
Отображения
Отображение 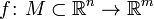 называется дифференцируемым в точке
называется дифференцируемым в точке 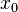 своей области определения
своей области определения 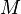 , если существует такое линейное отображение
, если существует такое линейное отображение 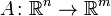 , зависящее от точки
, зависящее от точки 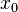 , что для любой точки
, что для любой точки 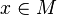 верно
верно
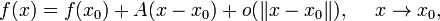 то есть, раскрывая символ «o» малое, если
то есть, раскрывая символ «o» малое, если
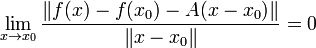 .
.
Линейное отображение 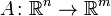 является дифференциалом отображения
является дифференциалом отображения 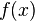 в точке
в точке 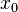 .
.
Если отображение 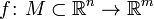 задано набором функций
задано набором функций 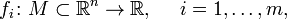
то его дифференцируемость в точке 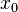 равносильна дифференцируемости всех функций в данной точке, и матрица его дифференциала
равносильна дифференцируемости всех функций в данной точке, и матрица его дифференциала 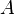 — это матрица Якоби, составленная из частных производных этих функций в точке
— это матрица Якоби, составленная из частных производных этих функций в точке 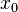 .
.
.
47.остновные правила дифференцированния
1) Производная от суммы равна сумме производных: 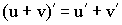
Доказательство:
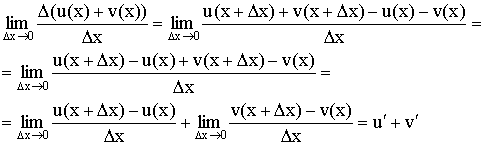
2) Постоянный множитель выносится за знак производной: 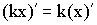 .
.
3) Производная произведения: 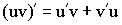 .
.
Доказательство:
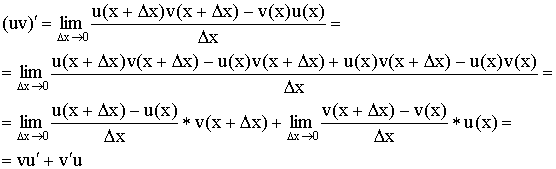
4) Производная дроби: 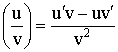 .
.
Доказательство:
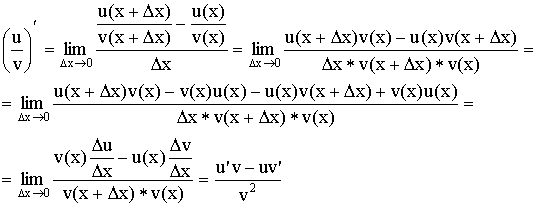
Вывод формул для производных.
1) 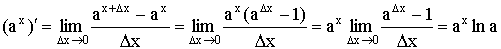
2) 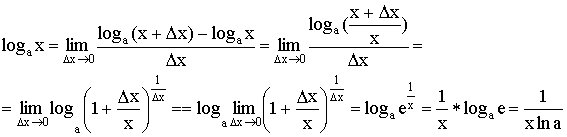
3) 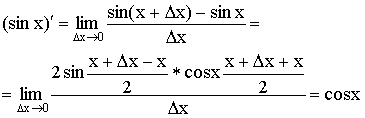
4) 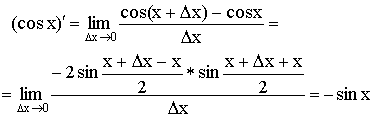
5) 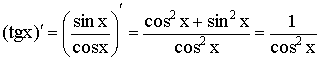
6) 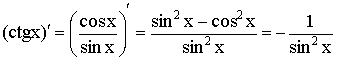
7) 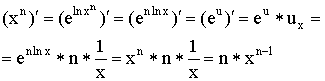
8) 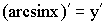
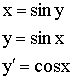
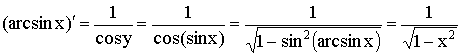
9) 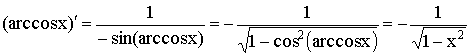
10) 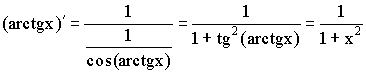
11) 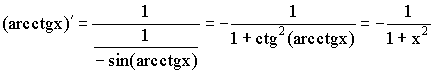
48.производные от элементарных функций
| Функция y = f(x) | Производные элементарных функций простого аргумента |
| y=xn | y  =n =n  xn−1 xn−1
|
| y = x | y  =1 =1
|
y= 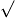 x x
| y  =12 =12 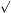 x x
|
| y=x1 | y  =−1x2 =−1x2
|
| y = cos x | y  =−sinx =−sinx
|
| y = sin x | y  =cosx =cosx
|
| y = tg x | y  =1cos2x =1cos2x
|
| y = ctg x | y  =−1sin2x =−1sin2x
|
| y = arcsin x | y  =1 =1 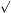 1−x2 1−x2
|
| y = arccos x | y  =−1 =−1 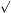 1−x2 1−x2
|
| y = arctg x | y  =11+x2 =11+x2
|
| y = arcctg x | y  =−11+x2 =−11+x2
|
y=ax  a a 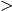 0 0  a a  =1 =1
| y  =ax =ax  lna lna  a a 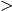 0 0  a a  =1 =1
|
| y=ex | y  =ex =ex
|
y=logax  a a 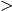 0 0  a a  =1 =1
| y  =1x =1x  lna lna
|
| y = lnx | y  =x1 =x1  x x 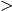 0 0
|
| Функция y = f(kx +b) | Функция y = f(kx +b) |
| y=(kx+b)n | y=(kx+b)n |
| y=(kx+b) | y=(kx+b) |
y= 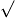 kx+b kx+b
| y= 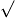 kx+b kx+b
|
| y=1kx+b | y=1kx+b |
| y = cos (kx +b) | y = cos (kx +b) |
| y = sin (kx +b) | y = sin (kx +b) |
| y = tg (kx +b) | y = tg (kx +b) |
| y = ctg (kx +b) | y = ctg (kx +b) |
| y = arcsin (kx +b) | y = arcsin (kx +b) |
| y = arccos (kx +b) | y = arccos (kx +b) |
| y = arctg (kx +b) | y = arctg (kx +b) |
| y = arcctg (kx +b) | y = arcctg (kx +b) |
y=akx+b  a a 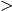 0 0  a a  =1 =1
| y=akx+b  a a 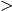 0 0  a a  =1 =1
|
| y=ekx+b | y=ekx+b |
y=loga(kx+b)  a a 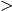 0 0  a a  =1 =1
| y=loga(kx+b)  a a  0 0  a a  =1 =1
|
| y = ln(kx +b) | y = ln(kx +b) |
49.производные сложной функции. Логарифмическая производная.
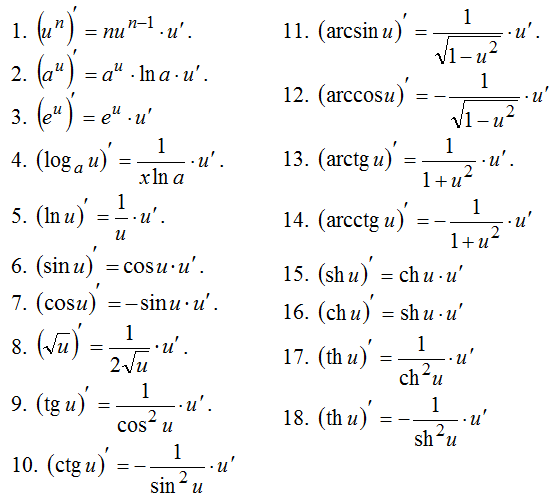
Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: 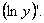
Используя формулу производной сложной функции, найдем, что
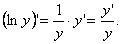 (*)
(*)
50. производная заданная в неявнои и параметрическом виде
Предположим, что функциональная зависимость 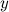 от
от  не задана непосредственно
не задана непосредственно 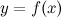 , а через промежуточную величину —
, а через промежуточную величину — 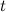 . Тогда формулы
. Тогда формулы
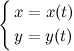
задают параметрическое представление функции одной переменной.
Пусть функция 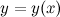 задана в параметрической форме, то есть в виде:
задана в параметрической форме, то есть в виде:
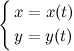 где функции
где функции 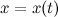 и
и 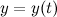 определены и непрерывны на некотором интервале изменения параметра
определены и непрерывны на некотором интервале изменения параметра 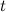 . Найдем дифференциалы от правых и левых частей каждого из равенств:
. Найдем дифференциалы от правых и левых частей каждого из равенств:
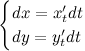
Далее, разделив второе уравнение на первое, и с учетом того, что 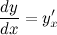 , получим выражение для первой производной функции, заданной параметрически:
, получим выражение для первой производной функции, заданной параметрически:
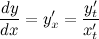
Для нахождения второй производной 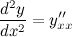 выполним следующие преобразования:
выполним следующие преобразования:
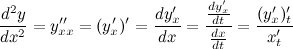
Рассмотрим функцию 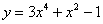
Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция 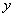 в явном виде выражена через независимую переменную
в явном виде выражена через независимую переменную 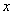 .
.








