Функции одной переменной] График функции (чёрная кривая) и касательная прямая (красная прямая)
Функция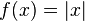 
и её производная.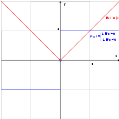 
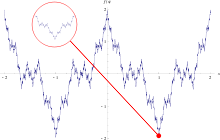График функции Вейерштрасса на интервале [−2, 2]. Этот график имеетфрактальный характер: зум (в красном круге) подобен всему графику.
Функция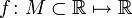 
одной переменной является дифференцируемой в точке 
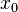своей области определения 
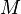, если существует такая константа 
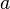, что для любой точки 
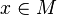верно
|
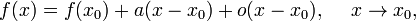
при этом число 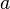неизбежно равно производной
|
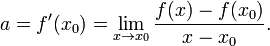
Функция одной переменной является дифференцируемой в точке 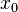тогда и только тогда, когда она имеет производную в этой точке.
График функции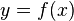 
представляет собой кривую на плоскости 
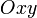, а график линейной функции
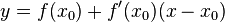
доставляет касательную прямую к этой кривой, проведённую в точке .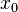
Напр., функция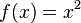 
определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде
.
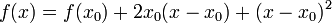При этом её производная есть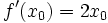 
, а уравнение касательной прямой, проведённой в точке 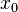, имеет вид: 
.
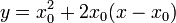Элементарные функции могут быть непрерывны в некоторой точке, но не быть в ней дифференцируемы. Напр., функция 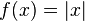является непрерывной на всей вещественной оси, но её производная испытывает скачок при переходе через точку 
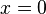, в котором эта функция не является дифференцируемой. В этой точке нельзя провести и касательную к графику функции. Функция 
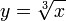тоже непрерывна на всей вещественной оси и её график имеет касательные во всех точках, однако касательная, проведённая в точке 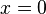, является вертикальной прямой и поэтому производная функции 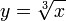бесконечно велика в точке 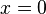, а сама функция не дифференцируема в этой точке.
Графики элементарных функций учат, что произвольная функция дифференцируема всюду, за исключением исключительных и изолированных значений аргумента. Первая попытка аналитического доказательства этого утверждения принадлежит Амперу[4], и поэтому оно носит название гипотезы Ампера. Это утверждение, однако, не верно в классе аналитически представимых функций, напр., функция Дирихле не является даже непрерывной ни в одной точке[5]. Нельзя также считать и произвольную непрерывную функцию дифференцируемой, напр., функция Вейерштрасса определена и непрерывная на всей вещественной оси, но не является дифференцируемой ни в одной её точке[6]. Это в частности означает, что к её графику ни в одной точке нельзя провести касательную прямую. Тем не менее, гипотезу Ампера можно рассматривать как нестрогую формулировку следующей теоремы Лебега: любая монотонная функция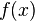 
имеет определённую конечную производную всюду, кроме, быть может, некоторого множества значений 
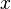меры нуль.[7]