Для функции точка - точка разрыва второго рода, так как .Точка устранимого разрыва
Определение
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции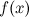 
в точке 
: 
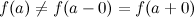или функция 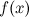не определена в точке , то точка называется точкой устранимого разрыва.
Пример
Рассмотрим функцию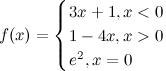 
. Найдем односторонние пределы и значение функции в точке 
:
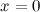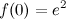
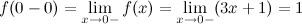
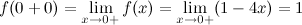
Так как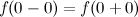 
и не равны значению функции в точке, то точка 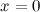- точка устранимого разрыва.
45.Производная функции, ее геометрический и механический смысл.
Производной функции y = f(x) в точке Х называется предел, если он существует, отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Производная функции в точке интерпретируется:
1. механически – как мгновенная скорость изменения функции в этой точке
2. геометрически – как угловой коэффициент касательной к графику функции в этой точке.
Механический смысл:
Зная закон S = f(t) движения точки, найти V ее движения в любой момент времени. Зафиксируем момент времени t и t + Dt;
За время t точка пройдет S(t), за t + Dt = s(t + Dt) – f(x)
За время Dt ® DS = f(t + Dt) – f(t)
Отношение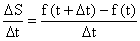 
- характеризует среднюю скорость Vср. за Dt
Если в этом отношении перейти к пределу при Dt ® 0, то получим истинную (мгновенную) скорость движения точки в момент t:
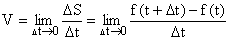
Геометрический смысл:
геометрически производная представляет собой угловой коэффициент касательной к графику этой функции.
Уравнение искомой касательной запишем в виде уравнения прямой, проходящей через т.М(Х0, У0), т.е.
У-У0 = к(Х-Х0), где неизвестен только коэф. – к, равный тангенсу угла наклона касательной к положительному направлению оси ОХ. Т.о. задача свелась к нахождению к = tga
Пусть кривая L задана функцией y = f(x), МТ – касательная к кривой в т.М(Х0, У0). На кривой L возьмем производную т.W(Х0+DХ, У0+DУ) и проведем секущую MW. Из тр-ка МКW определим угловой коэф-т секущей MW: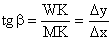 
Если W ® М, то b ® a и tgb ® tga, Þ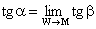 
, а т.к. при W ® М Dх ® 0, то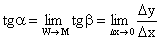 
Согласно определению, для отыскания производной функции y = f(x) в т.Х необходимо проделать 4 операции:
1. придать Х приращение DХ, т.е. перейти к точке Х+DХ
2. вычислить приращение функции DУ = f(Х+DХ)-f(X)
3. составить соотношение DУ/DХ
4. вычислить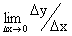 
46. понятие о дифференцированности функции
Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке)