Принцип максимума Понтрягина
Необходимость в принципе максимума Понтрягина возникает в случае, когда нигде в допустимом диапазоне управляющей переменной невозможно удовлетворить необходимому условию (3), а именно 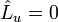 .
.
В этом случае условие (3) заменяется на условие (6):
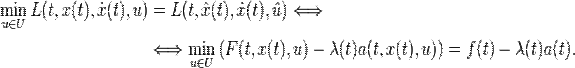
В этом случае согласно принципу максимума Понтрягина величина оптимального управления равна величине управления на одном из концов допустимого диапазона. Уравнения Понтрягина записываются при помощи функции Гамильтона Н, определяемой соотношением 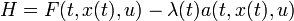 .
.
Из уравнений следует, что функция Гамильтона H связана с функцией Лагранжа L следующим образом: 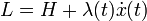 .
.
Подставляя L из последнего уравнения в уравнения (3-5) получаем необходимые условия, выраженные через функцию Гамильтона:
· уравнение управления по u: 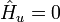 , (7)
, (7)
· уравнение состояния: 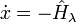 , (8)
, (8)
· сопряжённое уравнение: 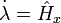 , (9)
, (9)
· трансверсальность по x: 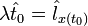 ,
, 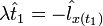 (10)
(10)
Необходимые условия, записанные в такой форме, называются уравнениями Понтрягина.
Где применяется
Принцип максимума особенно важен в системах управления с максимальным быстродействием и минимальным расходом энергии, где применяются управления релейного типа, принимающие крайние, а не промежуточные значения на допустимом интервале управления.
Метод динамического программирования
Метод динамического программирования основан на принципе оптимальности Беллмана, который формулируется следующим образом: оптимальная стратегия управления обладает тем свойством, что каково бы ни было начальное состояние и управление в начале процесса последующие управления должны составлять оптимальную стратегию управления относительно состояния, полученного после начальной стадии процесса.
http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5#.D0.97.D0.B0.D0.B4.D0.B0.D1.87.D0.B0_.D0.BE.D0.BF.D1.82.D0.B8.D0.BC.D0.B0.D0.BB.D1.8C.D0.BD.D0.BE.D0.B3.D0.BE_.D1.83.D0.BF.D1.80.D0.B0.D0.B2.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F- Оптимальное управление.
Математические основы оптимизации управления динамическими системами.
Уравнение Эйлера
Определение . Пусть М – некоторое пространство функций.
Отображение J: М → \1 называется функционалом.
Ниже будем рассматривать следующие пространства функций:
C[t1, t2] – непрерывные на отрезке [t1, t2] функции, с нормой, определенной следующим образом: ||x(⋅)||0 = max{ |x(t)|, t∈[t1, t2]}; C1[t1, t2] – непрерывно дифференцируемые на отрезке [t1, t2] функции, снормой ||x(⋅)||1 = max{ ||x(⋅)||0, ||x'(⋅)||0}. Простейшая задача вариационного исчисления формулируетсяследующим образом: найти экстремум функционала видаJ(x(⋅)) = F t x x dttt∫21( , , ') (1.1) на множестве кусочно-гладких функций x(⋅), соединяющих точки (t1, x1) и(t2, x2), т.е. удовлетворяющих краевым условиям x(t1) = x1; x(t2) = x2. Функции x(⋅), удовлетворяющие ограничениям задачи (в данном случае граничным условиям), называются допустимыми. Определение . Говорят, что x*(⋅) доставляет слабый локальныймаксимум функционалу J, если ∃ ε > 0: для любой допустимой кривой x(⋅), такой, что || x*(⋅) – x(⋅)||1 < ε, выполнено: J(x(⋅)) ≤ J(x*(⋅)). Говорят, что x*(⋅) доставляет сильный локальный максимум функционалуJ, если ∃ ε > 0: для любой допустимой кривой x(⋅), такой, что || x*(⋅) – x(⋅)||0< ε, выполнено J(x(⋅)) ≤ J(x*(⋅)). Необходимое условие слабого экстремума функционала (1.1) даетсяуравнением Эйлера: Fx – Fx 'dtd = 0. (1.2) Гладкое решение уравнения Эйлера называется экстремалью функционала J. Сотсков А.И., Колесник Г.В. Управление динамическими системами в задачах экономики:
Примеры:
Найти экстремаль в задаче: J = t x tx dt ∫+212 2( ' ' ) ; x(1) = a; x(2) = b.
Решение :
F(t, x, x') = t2x' + tx'2 , Fx = 0, Fx' = t2 + 2tx'. Составимуравнение Эйлера: Fx – Fx 'dtd = 2t + 2x' + 2 tx'' = 0. Видно, что в это уравнение не входит х. Обозначим у = x', тогда y' = x'' иуравнение примет видt + у + tу' = 0. Решением данного уравнения является у(t) = c/t – t/2. Тогдаx(t) = y t dt ∫( ) + d = c ln t – t2/4 + d. (1.3) Находя постоянные с и d из краевых условий, окончательно получаемx*(t) =ln2b− a+3/4ln t – t2/4 + a + 1/4. Функция x*(t) гладкая на [1, 2], следовательно, она является экстремалью. Замечание . В задаче с функционалом J = t x tx dt ∫+102 2( ' ' )экстремалиотсутствуют, так как решения уравнения Эйлера теряют гладкость наотрезке [0, 1].
http://crysalis.chat.ru/sample.pdf- Математические основы оптимизации
управления динамическими системами.
Многокритериальная оптимизация или программирование — это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.
Задача многокритериальной оптимизации встречаются во многих областях науки, техники и экономики.
Определени:
Задача многокритериальной оптимизации формулируется следующим образом:
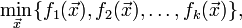
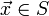
где 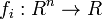 это
это 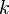 (
( 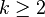 ) целевых функций. Векторы решений
) целевых функций. Векторы решений 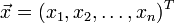 относятся к непустой области определения
относятся к непустой области определения 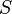 .
.
Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.
Эталонные точки
Для возможности оценки качества найденных решений обычно рассматривают такие точки в области значения целевой функции: идеальная точка 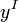 ,утопическая точка
,утопическая точка 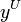 ,надир
,надир 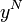 .
.
В некоторых случаях эти точки могут быть решениями.
Идеальная точка определяется как вектор 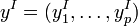 , каждая из координат которого имеет оптимальное значение соответствующей составляющей целевой функции:
, каждая из координат которого имеет оптимальное значение соответствующей составляющей целевой функции:
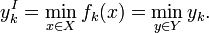
Точка надир 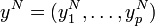 определяется как вектор:
определяется как вектор:
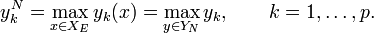
Утопическую точку 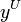 вычисляют на основе идеальной:
вычисляют на основе идеальной:
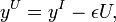
где 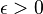 ,
, 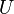 — единичный вектор.
— единичный вектор.
http://ru.wikipedia.org/wiki/%D0%9C%D0%BD%D0%BE%D0%B3%D0%BE%D0%BA%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F- Многокретериальная оптимизация.
Пример: « Покупка автомобиля »
| VW Golf | Opel Astra | Ford Focus | Toyota Corolla | |
| Цена (1000 Euro) | 16.2 | 14.9 | 14.0 | 15.2 |
| Расход топлива (на 100 км) | 7.2 | 7.0 | 7.5 | 8.0 |
| Мощность (kW) | 66.2 | 62.0 | 55.0 | 71.0 |
Какой автомобиль выбрать, чтобы он был мощным, недорогим, с малым расходом топлива?
Пример Opel и Ford
эффективный выбор или Парето*-оптимальный решения
X = fV W; Opel; F ord; T oyotag — допустимое множество
fi : X ! R, i = 1;2 — критерии оптимизации f = (f1; f2)
Y := f(X) := fy 2 R2: y = f(x) для x 2 Xg — образ множества X или допустимое множество в пространстве критериев minx2X(f1(x); f2(x))
http://math.nsc.ru/~alekseeva/TPR-FIT-2012/L6_fit.pdf








