Лабораторная работа № 3. 08
Муромский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича и
Николая Григорьевича Столетовых»
Кафедра: ФПМ Дисциплина: Физика
ЛАБОРАТОРНАЯ РАБОТА № 3.08
Утверждена на методическом семинаре кафедры ФПМ
Зав. кафедрой ____________
ТЕХНИКА БЕЗОПАСНОСТИ
1. Сборку и разборку схемы производить только при отключенном источнике питания.
2. Не включать собранную схему ,пока не изучите инструкцию по данном работе и не получите на это разрешение лаборанта или преподавателя.
3. Схема должна находиться под напряжением только во время регулировки и снятия показаний с приборов. КАТЕГОРИЧЕСКИ ЗАПРЕЩАЕТСЯ оставлять схему под напряжением без присмотра.
4. Строго соблюдать порядок выполнения работы, описаний и инструкций.
5. Па рабочем месте не должно быть посторонних предметов. Твердо знать, где расположен общий выключатель и порядок пользования им.
6. После окончания работы отключить источник питания, а затем разобрать схему и привести в порядок рабочее место.
Лабораторная работа № 3.08
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ И ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Приборы и принадлежности: микроскоп металлографический упрощенный ММУ-1, Микрометр MOB - 1 - 15, плосковыпуклая линза, плоскопараллельная пластина, светофильтры, источник тока на 6В.
ВВЕДЕНИЕ
1. ИНТЕФЕРЕНЦИЯ СВЕТА
Как известно, свет представляет собой электромагнитные волны. Уравнение волны имеет вид:
J=Acos(ωt-kx)
где А - амплитуда, ωt-kx - ее фаза, ω- угловая чистота.
K = π / λ ~ волновой вектор.
|
|
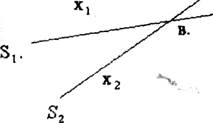
Допустим, что две монохроматические волны одинаковой частоты, распространяются в пространстве, накладываются друг на друга в некоторой точке пространства (рис.1). Уравнение волны:
|
y1=Acos(ωt-kx1); y2=Acos(ωt-kx2)
результирующую волну в точке В легко найти как результат наложения колебания обеих волн: у = y1+y2. Легко установить, что амплитуда результирующей волны равна:
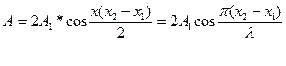
Она зависит от хода волн: D=X2-X1.
Если D = 2m(λ/2), где m= 0,1,2,... целое число, то амплитуда А=2А волны усиливают друг друга и точка В наблюдается максимум волны.
Если 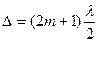 , где m = 0,1, 2,..., то амплитуда А (1). Будет равна нулю, наблюдается минимум интенсивности. Разность D =Х2-Х1 - есть геометрическая разность волн. Однако, при изучении оптических явлений часто приходится рассматривать оптическую длину пути l = пХ, где n - показатель преломления среды где распространяется свет и в соответствии с этим оптическую разность волн:
, где m = 0,1, 2,..., то амплитуда А (1). Будет равна нулю, наблюдается минимум интенсивности. Разность D =Х2-Х1 - есть геометрическая разность волн. Однако, при изучении оптических явлений часто приходится рассматривать оптическую длину пути l = пХ, где n - показатель преломления среды где распространяется свет и в соответствии с этим оптическую разность волн:
D= n2x2-n1x1 (2).
Условия обозревания максимумов и минимум освещенности (1) и (2) наблюдают только в случае наложения когерентных волн. Волны называются когерентными, если их разность фаз остается постоянной в течение достаточного длительного промежутка времени. В противном случае волны будут когерентными.
Интерференцией называется явление наложения когерентных волн друг на друга и образование при этом их взаимного усилия или ослабления..
От двух независимых источников света волны всегда будут некогерентными.
Для получения когерентных волн необходимо луч, идущий от какого - либо источника света разделить на два и заставить разделенные лучи накладываются друг на друга.
Это можно сделать с помощью зеркал Френеля, призмы Френеля, щелей Юнга и другими способами.
2. ИНТЕФЕРЕНЦИЯ В ТОНКИХ ПЛЕНКАХ.
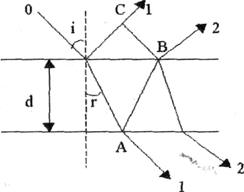
Представляем себе, что на тонкую прозрачную пленку толщиной d падает пучок параллельных
|
лучей (рис.2). Вследствие отражения от верхней и нижней грани пленки световой луч разделяется на два (1 и 2), которые являются когерентными и при наложении друг на друга будут интерферировать. Рассмотрим интерференцию лучей 1 и 2 в отвоженном сете. Оптическая разность хода их:
D=(OA+AB)*n-OC,
где n- показатель преломления вещества в пленке.
С обеих сторон находится воздух, для которого n=1. несложный расчеты дают, что
D =2dncos r (3) или 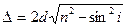 (3).
(3).
Где r - угол преломления, 1 - угол падения (см. рис.2).
Однако, следует иметь ввиду, что отражении света от верхней границы пленки происходит потеря полуволны. Поэтому эффективная разность хода волн равна:
D1=2dncos r –λ/2
При наложении лучей 1 и 2 наблюдается максимум, если
D1=2dncos r , D1=2m(λ/2)
или
D1=2dcos n =(2m+1)( λ/2) (4)
При выполнении условия D1 =(2m+1)( λ/2), m=0,1 ,2,...
Или 2dncos r =2m(λ/2) (5).
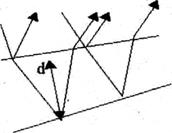
Образуется максимум освещенности. Для проходящего света условие (4) определяет максимум интенсивности света, а условие (5) - ее минимум. Как видно из формулы (3) и (3) разность хода волн зависит от двух факторов от толщены d и от угла падения лучей. В зависимости от этого различают, полосы равной толщены и полосы равного наклона. Полосы равной толщины, наблюдаются при освещении параллельными лучами клиновидной пластины (рис.3).
|
|
|
|
рис.3, рис.4.
Полосы равного наклона наблюдаются при освещении расходящимся световым пучком тонкой пленки с параллельными гранями (рис.4).
3. КОЛЬЦА НЬЮТОНА.
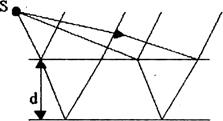
Классическим примером полос равной толщины, являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластины плоско - выпуклой линзы с большим радиусом кривизны (рис'.5). Роль тонкой пленки, от поверхности которой отражаются когерентные волны, играет воздушные зазор между пластинкой и линзой (вследствие большой толщины пластинки, и линзы за счет отражения от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при падении света по нормали к пластине. В том случае cos г =1 и оптическая разность хода по (3) равна удвоенной толщине пластинки:
D =2 h
в зазоре h~ 1. Очевидно (см. рис.5) R 2 =( R — h )2 + r 2 отсюда: 2h= r2/R
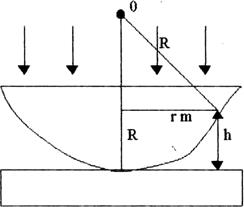
Рис.5.
Учитывая условие (4) образование интерференционных максимумов в отраженном свете, находим радиус m - го светового кольца.
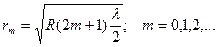 (6).
(6).
По условию (5), находим радиус m -го темного кольца в отраженном свете:
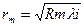 (7).
(7).
По формулам (6) и (7), зная λ, легко находится радиус кривизны линзы. Однако, невозможно добиться идеального соприкосновения поверхностей линзы и пластинки в одной точке. Но более правильным результат получается, если радиус кривизны линзы вычислять по разности квадратов радиусов двух колец. По формуле (7) для m -го темного кольца имеет:
rm 2 = Rmλ
для К -го кольца:
rk 2 = Rkλ
отсюда:
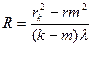 (8)-
(8)-
Формула (8) является расчетной формулой. Зная λ, по (8) находим R. Определив R, находим λ.
ОПИСАНИЕ ПРИБОРОВ.
1. МИКРОСКОП, (см. оптическую схему микроскопа). Источник света (1), лампочка накаливания (8-9В) - находится в фокусе двух линзового коллектора (2). При работе в светлом поле за коллектором устанавливается осветительная линза (3) и диафрагма (4). После линзы свет попадает на полупрозрачную пластинку (5) и частично отразившись от нее, попадает в объектив (6), пройдя объектив, свет попадает на объект (7), отражается от него и возвращается в объектив. Объект находится в фокусе объектива, поэтому лучи, вышедшие из объектива в виде параллельных, собираются линзой (8) и в фокальной плоскости окуляра (9). Остальные детали предназначены для работы в темном поле и в нашей работе не используются.
2. ОКУЛЯРНЫЙ МИКРОМЕТР ВИНТОВОЙ.
Окулярный микрометр одевается на тубус микроскопа вместо окуляра. С его помощью производится измерения величины изображения объектива. В фокальной плоскости окуляра микрометра расположена неподвижная стеклянная пластина со шкалой (от 0 до 8м), каждое деление, которое равно 1мм. В этой же плоскости расположена вторая неподвижная стеклянная пластина с перекрестием и виски перемещаются в поле зрения окуляра относительно неподвижной шкалы. Положением рисунка определяется целое число миллиметров, а по барабану отсчитывается сотые доли мм.
ВЫПОЛНЕНИЕ РАБОТЫ.
Включить прибор в сеть на 6В. приборы для получения колец Ньютона поставить на предметный стол против оси объектива. Вращая окуляр на закатанную часть, установить его на резкость изображения перекрестия. Глядя на объектив сбоку вращением винта грубой подачи опустить тубус микроскопа на столько, чтобы он не доходил до прибора для получения колец миллиметра на 2. затем, глядя в окуляр и вращая тот же винт, поднимать тубус до тех пор, пока не видны кольца Ньютона. Перемещая предметный столик совместим центр колец с центром ползрения. Перемещением рукоятки ирисовой диаграммы добиться более четкого изображения большого количества колец.
Упражнение 1. ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ.
За коллектором 2 вставить красный светофильтр с λ = 0.653 * 10-3 мм. Вращая барабан окуляра микрометра, установим его крест на середину ширины какого - нибудь достаточно удаленного от центра темного кольца, например, 8 -го и произвести то счет по шкале и барабану окулярного микрометра. Затем навести крест последовательно на 7 -е, 6 -е, и т. д. Кольца и произвести так же отчеты Пройдя центральное кольцо, продолжить отчеты в том же направлении, т.е. а право от центрального пятна, доходя до того же 8 -го кольца. Результаты занести в таблицу.
| № кольца.
| Отсчет микрометра.
| Разность отсчета.
| Диаметр кольца.
| Радиус кольца.
| |
| слева | справа | ||||
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| 8. | |||||
Из полученных от счетов определить диаметры, разделив разность отсчета на увеличение объектива (7.5), а затем и радиус кольца. Комбинируя попарно радиусы колец, по формуле (8) определить радиус кривизны линзы. При этом в целях повышения точности результата рекомендуется комбинировать радиусы колец так, чтобы разница составляла 4. Например 8 и 4 кольцо, 5 и 1 и так далее. Из полученных значений взять среднее арифметическое и найти среднюю абсолютную погрешность, относительную погрешность в %.
Упражнение 2. ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ.
Вместо красного светофильтра ставят зеленый светофильтр и проделывают то же, что и в упражнении 1 для 5 темных колец. Длину волны находят из формулы (7), подставив среднее значение радиуса кривизны линзы, найденное в упражнении 1.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Что такое интерференция света?
2. Какие волны называются когерентными?
3. Расскажите об интерференции света в тонких пленках. Как осуществить такую интерференцию?
4. Что такое полосы равного наклона и полосы равной толщены?
5. Расскажите о кольцах Ньютона.
6. Выведите формулу (3), (4), (7), (8).
ЛИТЕРАТУРА.
1. И.В. Савельев. Курс общей физики. "Наука", М.: 1971г. т. 3 стр. 78 -99.
2. Г.А. Зисман и О.М. Тодес. Курс общей физики. "Наука", И.: 1970г. т.З стр. 67 - 87.
3. А.И. Китайгородский. "Введение в физику". "Наука". М.: 1973г. стр. 312 - 323.