Санкт-Петербургский государственный
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
отчет
по лабораторной работе №2
по дисциплине «Физико-химические основы технологии изделий электроники и наноэлектроники»
Тема: Моделирование диаграмм состояния с ограниченной растворимостью компонентов (полупроводник - примесь)
| Студенты гр. 6209 | Тойкка А.С. | |
| Богданова М.В. | ||
| Гребнев К.В. | ||
| Преподаватель | Мараева Е. В. |
Санкт-Петербург
2018
Цель работы.
Изучение фазовых равновесий в бинарной системе Ge-Ag путём компьютерного моделирования; расчет параметров межатомного взаимодействия; выбор моделей растворов, адекватно описывающих экспериментальные Т-х-диаграммы состояния; расчет спинодалей и определение областей устойчивого и метастабильного состояний твердых растворов в заданной системе.
Исходные данные
Исходная T-x-проекция фазовой диаграммы состояния системы A-B (Ge-Ag) представлена на рисунке 1.
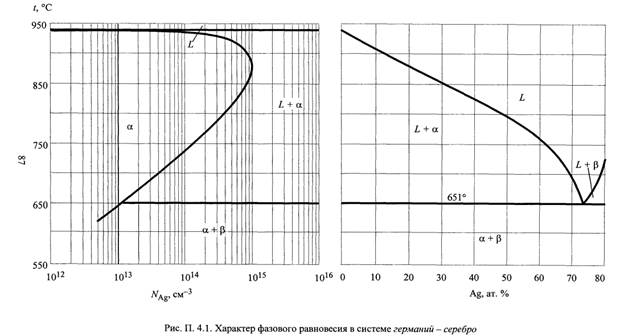
Рисунок 1 - Т-х-проекция диаграммы состояния системы Ge-Ag
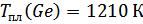
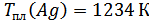
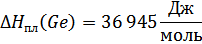
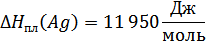
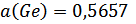
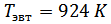
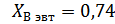
Обработка экспериментальных результатов
1. Привести Т-х-проекции исследованной диаграммы состояния. Оптимальные параметры межатомного взаимодействия Wsopt и Wlopt в твердом и жидком растворах соответственно.
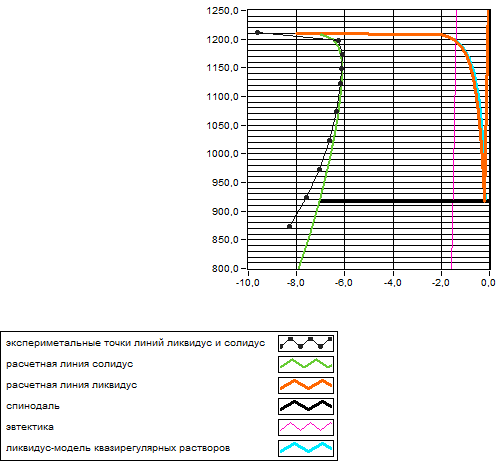
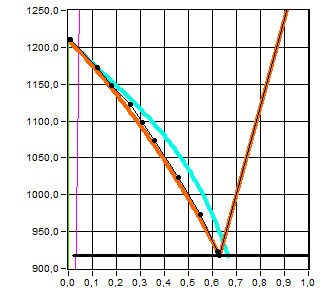
Рис. 2 . T-x-проекции экспериментальной и теоретически рассчитанной диаграмм состояния
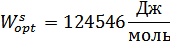

Как видно из графика, T-x-проекция теоретически рассчитанной диаграммы почти совпадает с экспериментальной. Различия можно объяснить неточностью определения экспериментальных точек ликвидуса и солидуса.
2. Расчет и построение линии ликвидуса в рамках модели идеального жидкого раствора и сравнение с линиями ликвидуса в рамках регулярного и квазирегулярного раствора.
ΔHпл(Ge)/Tпл(Ge)=ΔSпл(Ge)
xSGe = 1
Для идеального раствора уравнение:
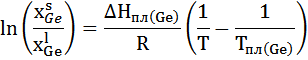
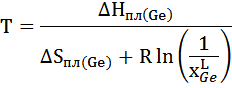
Аналогично для регулярного раствора:
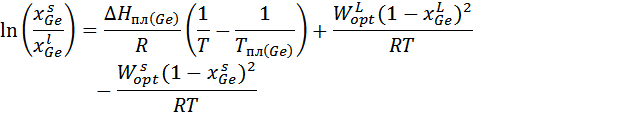
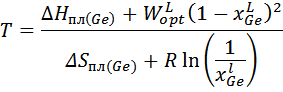
Для модели квазирегулярного раствора:
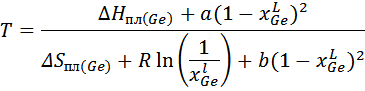
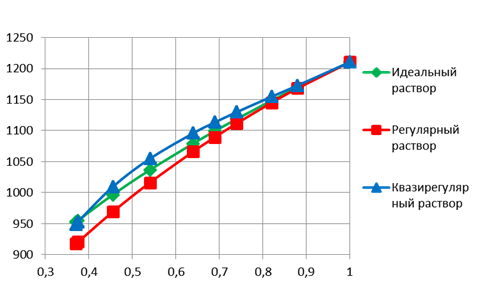
Рис. 3. Сравнение линии ликвидуса в разных моделях раствора.
Для описания жидких растворов лучше всего подходит модель квазирегулярных растворов, а для твёрдых растворов – модель регулярного раствора.
3. Расчет и построение концентрационной зависимости коэффициентов активностей компонентов в твердом растворе при Т=(Тпл( Ge )+ Тэвт)/2, а также в жидком растворе при Т = Тпл( Ge ).
Рассмотрим твёрдый раствор при температуре Т:
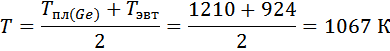
Коэффициент активности для твёрдого раствора: 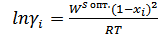
Таблица 1. Расчет для компонентов Ge и Cu для твердого раствора
| Xag | lnγGe | Xag | lnAg |
| 0,05 | 12,677 | 0,95 | 0,0351 |
| 0,1 | 11,378 | 0,9 | 0,1405 |
| 0,15 | 10,149 | 0,85 | 0,316 |
| 0,2 | 8,9897 | 0,8 | 0,5619 |
| 0,25 | 7,9011 | 0,75 | 0,8779 |
| 0,3 | 6,8827 | 0,7 | 1,2642 |
| 0,35 | 5,9346 | 0,65 | 1,7207 |
| 0,4 | 0 | 0,6 | 0 |
| 0,45 | 0 | 0,55 | 0 |
| 0,5 | 0 | 0,5 | 0 |
| 0,55 | 0 | 0,45 | 0 |
| 0,6 | 0 | 0,4 | 0 |
| 0,65 | 0 | 0,35 | 0 |
| 0,7 | 0 | 0,3 | 0 |
| 0,75 | 0,8779 | 0,25 | 7,9011 |
| 0,8 | 0,5619 | 0,2 | 8,9897 |
| 0,85 | 0,316 | 0,15 | 10,149 |
| 0,9 | 0,1405 | 0,1 | 11,378 |
| 0,95 | 0,0351 | 0,05 | 12,677 |
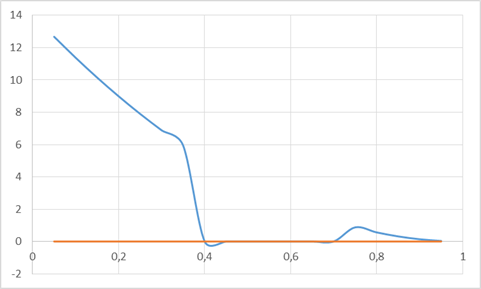
Рис. 4. Концентрационная зависимость коэффициента активности компонента Ge в твердом растворе
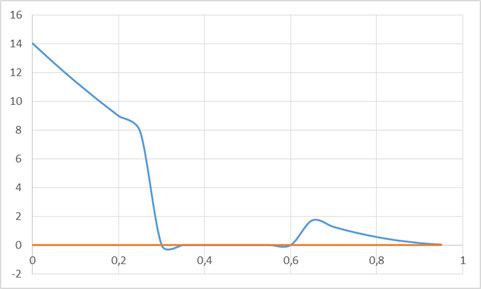
Рис. 5. Концентрационная зависимость коэффициента активности компонента Cu в твердом растворе
Рассмотрим жидкий раствор при температуре Т:
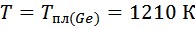
Коэффициент активности для твёрдого раствора: 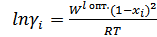
Таблица 2. Расчет для компонентов Ge и Ag для жидкого раствора
| Xag | lnγGe | Xag | lnAg |
| 0,05 | -0,308 | 0 | -0,342 |
| 0,1 | -0,277 | 0,05 | -0,308 |
| 0,15 | -0,247 | 0,1 | -0,277 |
| 0,2 | -0,219 | 0,15 | -0,247 |
| 0,25 | -0,192 | 0,2 | -0,219 |
| 0,3 | -0,167 | 0,25 | -0,192 |
| 0,35 | -0,144 | 0,3 | -0,167 |
| 0,4 | -0,123 | 0,35 | -0,144 |
| 0,45 | -0,103 | 0,4 | -0,123 |
| 0,5 | -0,085 | 0,45 | -0,103 |
| 0,55 | -0,069 | 0,5 | -0,085 |
| 0,6 | -0,055 | 0,55 | -0,069 |
| 0,65 | -0,042 | 0,6 | -0,055 |
| 0,7 | -0,031 | 0,65 | -0,042 |
| 0,75 | -0,021 | 0,7 | -0,031 |
| 0,8 | -0,014 | 0,75 | -0,021 |
| 0,85 | -0,008 | 0,8 | -0,014 |
| 0,9 | -0,003 | 0,85 | -0,008 |
| 0,95 | -0,001 | 0,9 | -0,003 |
| 1 | 0,000 | 0,95 | -0,001 |
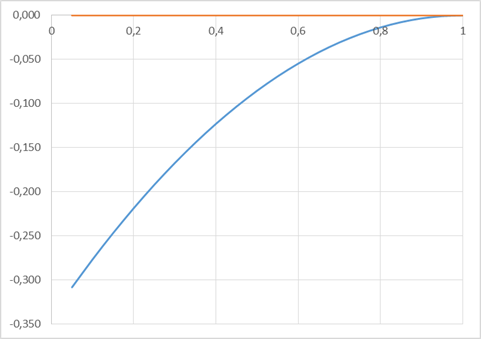
Рис. 6. Концентрационная зависимость коэффициента активности компонента Ge в жидком растворе
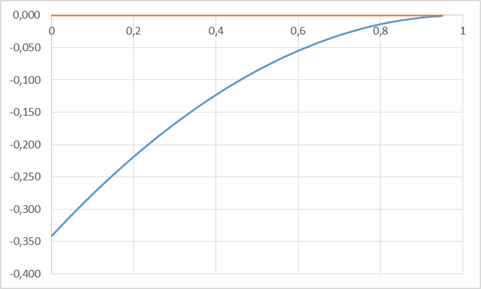
Рис. 7. Концентрационная зависимость коэффициента активности компонента Ag в жидком растворе
4. Используя Т-х-проекцию диаграммы состояния рассчитать равновесный коэффициент распределения компонента В (примесь) при :
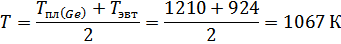
Учитывая, что 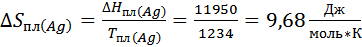
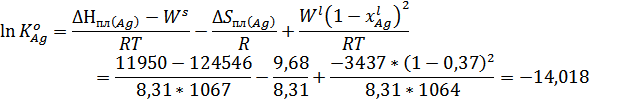
XAg=0,37 определили по фазовой диаграмме при температуре 1067К.
5. Рассчитать и построить спинодали при температурах от Ткомн до Тпл(А). Показать на крупномасштабной Т-х-диаграмме заданной системы области стабильных (равновесных), метастабильных и абсолютно неустойчивых твердых растворов.
Получаем уравнение для спинодалей путем приравнивания к нулю второй производной энергии Гиббса:
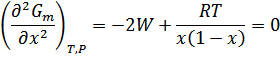
Следовательно,
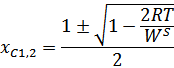
Так как по оси x возрастает атомная доля Ag, то для расчета спинодалей при растворе примеси Ag в Ge берем формулу со знаком минус перед корнем, а при растворе примеси Ge в Ag берем со знаком плюс.
Рис. 7. Линии спинодалей и области растворов.
Вывод
В общем случае активность компонентов при возрастании температуры экспоненциально уменьшается, а состав определяет то, как быстро происходит спад.
T-x-проекция теоретически рассчитанной диаграммы почти совпадает с экспериментальной. Для описания жидких растворов лучше всего подходит модель квазирегулярных растворов, а для твёрдых растворов – модель регулярного раствора.
Было получено, что для твёрдого и жидкого растворов энтальпия смешения HM˃0, но вместе с этим выполняется следующее |HM|<|TSM|, т.е. в уравнении GM=HM-TSM преобладает по значению энтропийный член, и свободная энергия раствора оказывается меньше свободной энергии механической смеси. В этом случае реализуется диаграмма состояния с непрерывной растворимостью компонентов в твёрдой и жидкой фазах.
Рассчитаны и построены концентрационные зависимости коэффициентов активности и активностей компонентов в твёрдом и жидком растворах при T=const. Активность компонентов при возрастании температуры экспоненциально уменьшается.








