В теории игр предполагается, что оба игрока действуют разумно, то есть стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим (для себя) образом.
2.2.1.1. Действия игрока A
1-й шаг. В каждой строке матрицы A ищется минимальный элемент
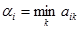, i = 1, 2, …, m.
Полученные числа a 1 , a 2 , …, a m приписываются к заданной таблице в виде правого добавочного столбца
| a 11 | a 12 | … | a 1n | a 1 |
| a 21 | a 22 | … | a 2n | a 2 |
| … | … | … | … | … |
| am 1 | am 2 | … | amn | a m |
Пояснение. Выбирая стратегию Ai, игрок A вправе рассчитывать на то, что в результате разумных действий противника (игрока В) он выиграет не меньше чем a i.
2-й шаг. Среди чисел a 1 , a 2 , …, a m выбирается максимальное число
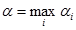
или, подробнее,
.
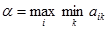Специально отметим, что выбранное число a является одним из элементов заданной матрицы А.
Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок A должен остановиться на той стратегии Аr, для которой число a i - является максимальным.
Если игрок A будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока B игроку A гарантирован выигрыш, не меньший a.
Число a называется нижней ценой игры.
Принцип построения стратегии игрока A, основанный на максимизации минимальных выигрышей, называется принципом максимина, а выбираемая в соответствии с этим принципом стратегия Ai0 — максиминной стратегией игрока А.
2.2.1.2. Действия игрока В
1-й шаг. В каждом столбце матрицы A ищется максимальный элемент
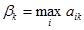, k = 1, 2, …, n.
Полученные числа b 1 , b 2 , …, b n приписываются к заданной таблице в виде нижней добавочной строки
| a 11 | a 12 | … | a 1n | a 1 |
| a 21 | a 22 | … | a 2n | a 2 |
| … | … | … | … | … |
| am 1 | am 2 | … | amn | a m |
| b 1 | b 2 | … | b n |
Пояснение. Выбирая стратегию Вk, игрок B должен рассчитывать на то, что в результате разумных действий противника (игрока А) он проиграет не больше чем βk.
2-й шаг. Среди чисел b 1 , b 2 , …, b n выбирается минимальное число
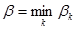
или, подробнее,
.
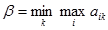Выбранное число β также является одним из элементов заданной матрицы А.
Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок B должен остановиться на той стратегии Вk, для которой число βk является минимальным.
Если игрок B будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока A игроку B гарантирован проигрыш, не больший β. Число β называется верхней ценой игры.
Принцип построения стратегии игрока B, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия Вk0 — минимаксной стратегией игрока В.
Нижняя цена игры a и верхняя цена игры β всегда связаны неравенством a ≤ β .
Замечание. Реализация описанного алгоритма требует 2тп - 1 сравнений элементов матрицы А:
(n - 1)m + т - 1 = тп - 1
сравнений для определения a,
(n - 1)m + т - 1 = тп - 1
сравнений для определения β и одно сравнение полученных чисел a и b.
Если
a = β,
или, подробнее,
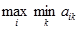= ai 0 k 0 =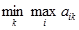 
то ситуация {Ai0, Bk0} оказывается равновесной, и ни один из игроков не заинтересован в том, чтобы ее нарушить.
В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называется просто ценой игры и обозначается через v.
Цена игры совпадает с элементом аi0k0 матрицы игры A, расположенным на пересечении i0 - й строки (стратегия Ai0 игрока А) и k0 - го столбца (стратегия Вk0 игрока В) — минимальным в своей строке и максимальным в своем столбце.
Этот элемент называют седловой точкой матрицы A, или точкой равновесия, а про игру говорят, что она имеет седловую точку.
Стратегии Аi0 и Вk0, соответствующие седловой точке, называются оптимальными, а совокупность оптимальных ситуаций и ценs игры — решением матричной игры с седловой точкой.
Замечание. Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.
Матричные игры с седловой точкой важны и интересны, однако более типичным является случай, когда применение описанного алгоритма приводит к неравенству a < β.
Как показывает следующий пример, в этом случае предложенный выбор стратегий уже, вообще говоря, к равновесной ситуации не приводит, и при многократном ее повторении у игроков вполне могут возникнуть мотивы к нарушению рекомендаций, основанных на описанном алгоритме действий игроков A и В.