Полученная матрица имеет размер m ´ n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).
2.1. МАТРИЧНЫЕ ИГРЫ
Рассмотрим игру, в которой участвуют два игрока, причем каждый из игроков имеет конечное число стратегий. Обозначим для удобства одного из игроков через A, в другого — через В.
Предположим, что игрок A имеет m стратегий — А1, А2, ... , Ат, а игрок B имеет n стратегий В1, В2,... , Вn.
Пусть игрок A выбрал стратегию Аi, а игрок B стратегию Вk. Будем считать, что выбор игроками стратегий Аi и Вk однозначно определяет исход игры — выигрыш aik игрока A и выигрыш bik игрока B, причем эти выигрыши связаны равенством
bik = - aik
(отрицательный выигрыш на бытовом языке обычно называют проигрышем).
Последнее условие показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с противоположным знаком. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.
Значения aik выигрыша при каждой паре стратегий (в каждой ситуации) {Ai, Вk}, i = 1, 2 ,..., т, k = 1, 2, ..., n (если они конечно нам известны), удобно записывать или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока A, а столбцы — стратегиям игрока В:
| B 1 | B 2 | … | Bn | |
| A 1 | a 11 | a 12 | … | a 1n |
| A 2 | a 21 | a 22 | … | a 2n |
| … | … | … | … | … |
| Am | am 1 | am 2 | … | amn |
или в виде матрицы
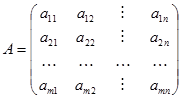
Полученная матрица имеет размер m ´ n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).
Рассматриваемую игру часто называют игрой m ´ n или m ´ n игрой.
Замечание. Матричные игры относятся к разряду так называемых антагонистических игр, то есть игр, в которых интересы игроков прямо противоположны.
2.1.1. Равновесная ситуация
Рассмотрим следующий пример.
Пример 1. Два игрока A и B, не глядя друг на друга, кладут на стол по картонному кружку красного (r), зеленого (g) или синего (b) цветов, сравнивают цвета кружков и расплачиваются друг с другом так, как показано в матрице игры
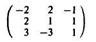
(напомним, что у этой 3 × 3-матрицы строки соответствуют стратегиям игрока A, а столбцы — стратегиям игрока B).
Считая, что эта 3 × 3 игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.
Начнем с последовательного анализа стратегий игрока A, не забывая о том, что, выбирая стратегию игрока A, должно принимать в расчет, что его противник B может ответить на нее той из своих стратегий, при которой выигрыш игрока A будет минимальным.
Так, на стратегию Ar он ответит стратегией Вr (минимальный выигрыш равен -2, что на самом деле означает проигрыш игрока A, равный 2), на стратегию Ag — стратегией Bg или Вb (минимальный выигрыш игрока A равен 1), а на стратегию Аb — стратегией Bg (минимальный выигрыш игрока А равен -3).
Запишем эти минимальные выигрыши в правом столбце таблицы:

Maxmin. Неудивительно, что игрок A останавливает свой выбор на стратегии Ag, при которой его минимальный выигрыш максимален (из трех чисел -2, 1 и -3 максимальным является 1):
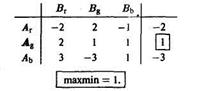
Если игрок A будет придерживаться этой стратегии, то ему гарантирован выигрыш, не меньший 1, при любом поведении противника в игре.
Аналогичные рассуждения можно провести и за игрока B. Так как игрок B заинтересован в том, чтобы обратить выигрыш игрока A в минимум, то ему нужно проанализировать каждую свою стратегию с точки зрения максимального выигрыша игрока A.
Выбирая свою стратегию, игрок B должен учитывать, что при этом стратегией его противника A может оказаться та, при которой выигрыш игрока A будет максимальным. Так, на стратегию Вr он ответит стратегией Аr (максимальный выигрыш игрока A равен 3), на стратегию Bg — стратегией Аr (максимальный выигрыш игрока A равен 2), а на стратегию Вb — стратегией Ag или Аb (максимальный выигрыш игрока A равен 1). Эти максимальные выигрыши записаны в нижней строке таблицы

Minmax . Неудивительно, если игрок B остановит свой выбор на стратегии Вb, при которой максимальный выигрыш игрока A минимален (из трех чисел 3, 2 и 1 минимальным является 1):

Если игрок B будет придерживаться этой стратегии, то при любом поведении противника он проиграет не больше 1.
В рассматриваемой игре числа maxmin и minmax совпали:
maxmin = minmax = 1
(соответствующие элементы в таблице выделены жирным шрифтом).

Выделенные стратегии Ag и Вb являются оптимальными стратегиями игроков A и B,
Ag = Aopt, Bg = Bopt,
в следующем смысле:
при многократном повторении игры отказ от выбранной стратегии любым из игроков уменьшает его шансы на выигрыш (увеличивает шансы на проигрыш).
В самом деле, если игрок A будет придерживаться не стратегии Aopt, а выберет иную стратегию, например, Ar, то вряд ли стоит рассчитывать на то, что игрок B этого не заметит. Конечно, заметит и не преминет воспользоваться своим наблюдением. Ясно, что в этом случае он отдаст предпочтение стратегии Br. А на выбор Аb игрок B ответит, например, так – Bg. В результате отказа от стратегии Ag выигрыш игрока A уменьшится.
Если же от стратегии Bopt отказывается игрок B, выбирая, например, стратегию Вr, то игрок A может ответить на это стратегией Ab и, тем самым, увеличить свой выигрыш. В случае стратегии Bg ответ игрока A — Ar.
Тем самым, ситуация {Аg, Вb} оказывается равновесной.
Еще раз подчеркнем, что элементами матрицы игры являются числа, описывающие выигрыш игрока А. Более точно, выигрыш соответствует положительному элементу платежной матрицы, а отрицательный указывает на проигрыш игрока А.
Матрица выплат игроку B получается из матрицы игры заменой каждого ее элемента на противоположный по знаку.
Рассмотрим теперь произвольную матричную игру
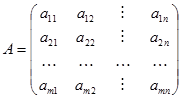
(строки заданной т × n - матрицы соответствуют стратегиям игрока A, а столбцы — стратегиям игрока B) и опишем общий алгоритм, посредством которого можно определить, есть ли в этой игре ситуация равновесия или ее нет.








