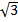Домашнее задание 3( 4 апреля)
1)В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 20 % от стоимости купленной мебели. Шкаф стоит 4100 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
2
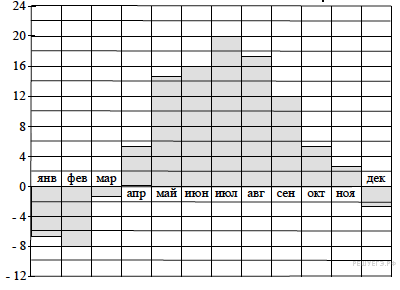
2)На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, в каком месяце среднемесячная температура впервые превысила 14 °С. В ответе запишите номер месяца. (Например, ответ 1 обозначает январь.)
3)В магазине три продавца. Каждый из них занят обслуживанием клиента с вероятностью 0,7 независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты.
4)Найдите корень уравнения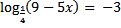 
5)В равнобедренном треугольнике ABC с основанием AB боковая сторона равна 
16 
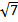Найдите длину высоты AH.
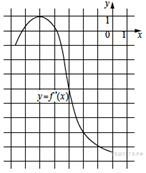
6)На рисунке изображён график функции f '(x) — производной функции f(x) Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y = 10 -7x или совпадает с ней.
7)Даны два цилиндра. Объём первого цилиндра равен 8. У второго цилиндра высота в 4 раза меньше, а радиус основания в 3 раза больше, чем у первого. Найдите объём второго цилиндра.
8)Найдите значение выражения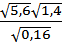 
10.Автомобиль, масса которого равна m = =2000 кг, начинает двигаться с ускорением, которое в течение t секунд остаётся неизменным, и проходит за это время путь S = 1000 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю (тяги двигателя), равно F=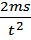 
Определите время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, равна 1600 Н. Ответ выразите в секундах.
11).По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 900 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте 3 секундам. Ответ дайте в метрах.
12)Найдите точку минимума функции y =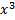 
-4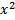 
–x- 13
13)а) Решите уравнение 
- 
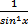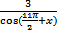= -2
б) Укажите корни этого уравнения, принадлежащие отрезку [-2π; -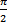 
]
14В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 5 и диагональю BD = = 9 .Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 4.
а) Докажите, что плоскость CEF параллельна ребру SB .
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
15.Решите неравенство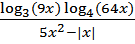 
16.Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что ∟ВАС= 30o
б) Пусть прямые MK и BC пресекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC = 2 