Домашнее задание 2 (3 апреля)
Домашее задание1 (2апреля)
Алгебра
Тема Уравнения и неравенств с двумя пе6ременными
Изучить материал п 58 решить задачи № 58.2-58.6
Тема: системы уравнений
Изучить материал п 59 решить задачи № 59.3-59.6
Геометрия
Тема: Объем шара
Изучить матриал п 82-83 решить задачи 716, 719
Домашнее задание 2 (3 апреля)
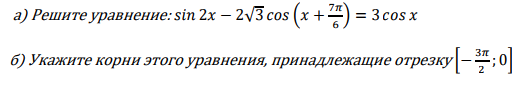
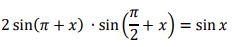
б) Найдите все корни этого уравнения, принадлежащие отрезку 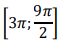
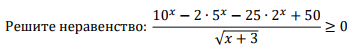
Текстовые задачи
1. Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 м забора. Определите, сколько дней бригада маляров красила весь забор?
2. Из пункта А в пункт Б одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч. А вторую половину пути со скоростью, на 16 км/ч больше скорости первого, в результате чего прибыл в пункт Б одновременно с первым автомобилем. Найдите скорость первого автомобиля.
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравнялись в первый раз, если скорость одного на 21 км/с больше скорости.
4. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
5. Заказ на изготовление 11- деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий. Если известно, что первый за час изготавливает на 1 деталь больше?
6. Имеется два сплава. Первый содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько масса первого сплава меньше массы второго?
1)Найдите значение выражение: (8 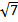 + 4)( 8
+ 4)( 8 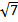 – 4)
– 4)
2) решите уравнение Lg(-4x-30) = 2
3) Найти значение выражения 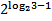
4) решить уравнение 4(-7-x) -5x = 8
4)В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC=80 и BC=BM. Найдите AH.
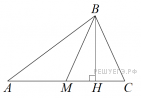
6) Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого
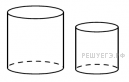
7) Найдите значение выражения ( 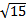 -8)(
-8)( 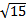 + 8) = ?
+ 8) = ?
8) Найдите корень уравнения 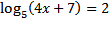
9)Каждому из четырёх графиков функций в первом перечне соответствует одно из значений производной функции f(x) в точке xo во втором перечне. Установите соответствие между графиками и значениями производной.
ГРАФИКИ
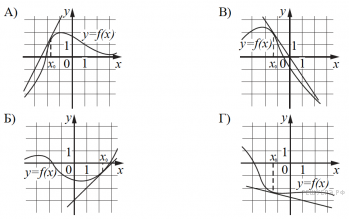
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ 1) -3/2; 2) -1/4; 3) 1; 4) 2
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г |
Задание 14 № 511658
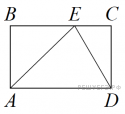
10)На стороне ВС прямоугольника ABCD , у которого AB=8 и AD=14, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
11) Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

12)Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) 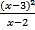 > 0
Б) (x-2)(x-3) < 0
В) > 0
Б) (x-2)(x-3) < 0
В) 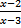 > 0
Г) (x-2)2 (x-3) < 0 > 0
Г) (x-2)2 (x-3) < 0
| 1) (-∞; 2) (3; +∞) 2) (2;3) (3; +∞) 3) (2;3) 4) (-∞; 2) ( 2;3) |
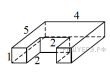
13 На рисунке изображён многогранник (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этого многогранника. Ответ дайте в кубических сантиметрах.
14)В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC=80 и AB=BC. Найдите BH

15)Даны два цилиндра. Радиус основания и высота первого равны соответственно 15 и 6, а второго — 2 и 5. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

16)Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) (x-1)2 (x-6) < 0
Б) 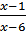 > 0
В) (x-1)(x-6) < 0
Г) > 0
В) (x-1)(x-6) < 0
Г) 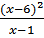
| 1) (1; 2) 2) (-∞; 1) ( 6; +∞) 3) (-∞; 1)( 1;6) 4) (1;6)(6;+∞) |
17) найти корни уравнения 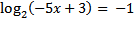
18)В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
19)Каждому из четырёх графиков функций в первом перечне соответствует одно из значений производной функции f(x) в точке xo во втором перечне. Установите соответствие между графиками и значениями производной.
ГРАФИКИ
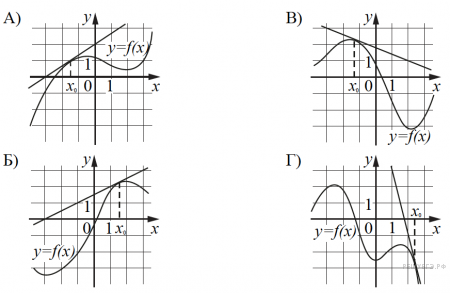
1) 2/3; 2) -2/5; 3) ½; 4) -4
20) В треугольнике ABC проведены медиана BM и высота BH . Известно, что AB=BM и AC=28. Найдите AH.

21)Стороны основания правильной шестиугольной пирамиды равны 10, боковые рёбра равны 13. Найдите площадь боковой поверхности этой пирамиды.
22) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) (x-3)(x-4)< 0
Б) 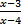 > 0
В) (x-3) 2 (x-4) < 0
Г) > 0
В) (x-3) 2 (x-4) < 0
Г) 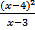 > 0 > 0
| 1) (-∞; 3) (4; +∞) 2) (3;4) (4; +∞) 3) (3; 4) 4) (-∞; 3) ( 3; 4) |
23) найти значение выражения 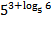
24) решить уравнение -2(-5-3x) – 5x = -2
25) В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 60 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.

26)На стороне BC прямоугольника ABCD , у которого AB=72 и AD=93, отмечена точка E так, что угол EAB = 45o. Найдите ED

27) Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2 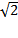 , а высота равна 2..
, а высота равна 2..
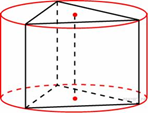
28) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
A) (x-2) 2 (x-4) > 0 1) (-∞; 2) (2; 4)
Б) 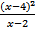 > 0 2) (- ∞; 2) ( 4; +∞)
> 0 2) (- ∞; 2) ( 4; +∞)
В) (x-2) (x-4) < 0 3) ( 2; 4)
Г) 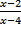 > 0 4) (2 ; 4) (4; +∞)
> 0 4) (2 ; 4) (4; +∞)








