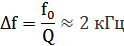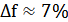5 Формирование эквидистантной антенной решетки

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

В настоящей ВКР требуется произвести формирование эквидистантного расположения приемно-излучающих элементов. Для решения данной задачи будет задействован «Метод решетки», впервые описанный в работе [9]. Метод предполагает расположение элементов по принципу, который описывает следующее выражение:

;

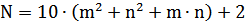(1)

Где N – количество точек на сфере, m и n – натуральные числа.

Введя на комплексной оси плоскости косоугольную систему координат с ортам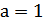и и 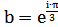, получим новую систему координат с осями, образующими угол 60^о и порождающими на плоскости целочисленную решетку 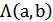, узлами которой будет множество концов всевозможных векторов, имеющих целочисленные координаты и начало в точке (0,0).

Далее рассмотрим 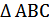с вершинами в узлах 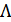: 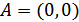, 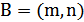и 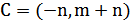. Выбранный таким образом треугольник оказывается равносторонним при подстановке любой пары чисел m и n.

Для построения требуемого размещения точек далее требуется зафиксировать все точки решетки, которые попали внутрь полученного треугольника, включая его вершины и точки, попавшие на стороны треугольника, (Рисунок 5.1).

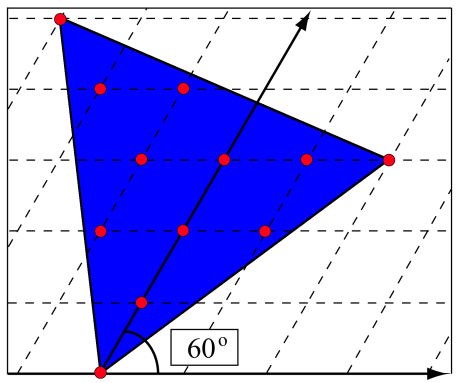
Рисунок 5.1 - Равносторонний треугольник с вершинами в узлах решетки

Отразим полученное множество точек на каждую грань вписанного в сферу икосаэдра, грани которого полностью совпадают с треугольником .

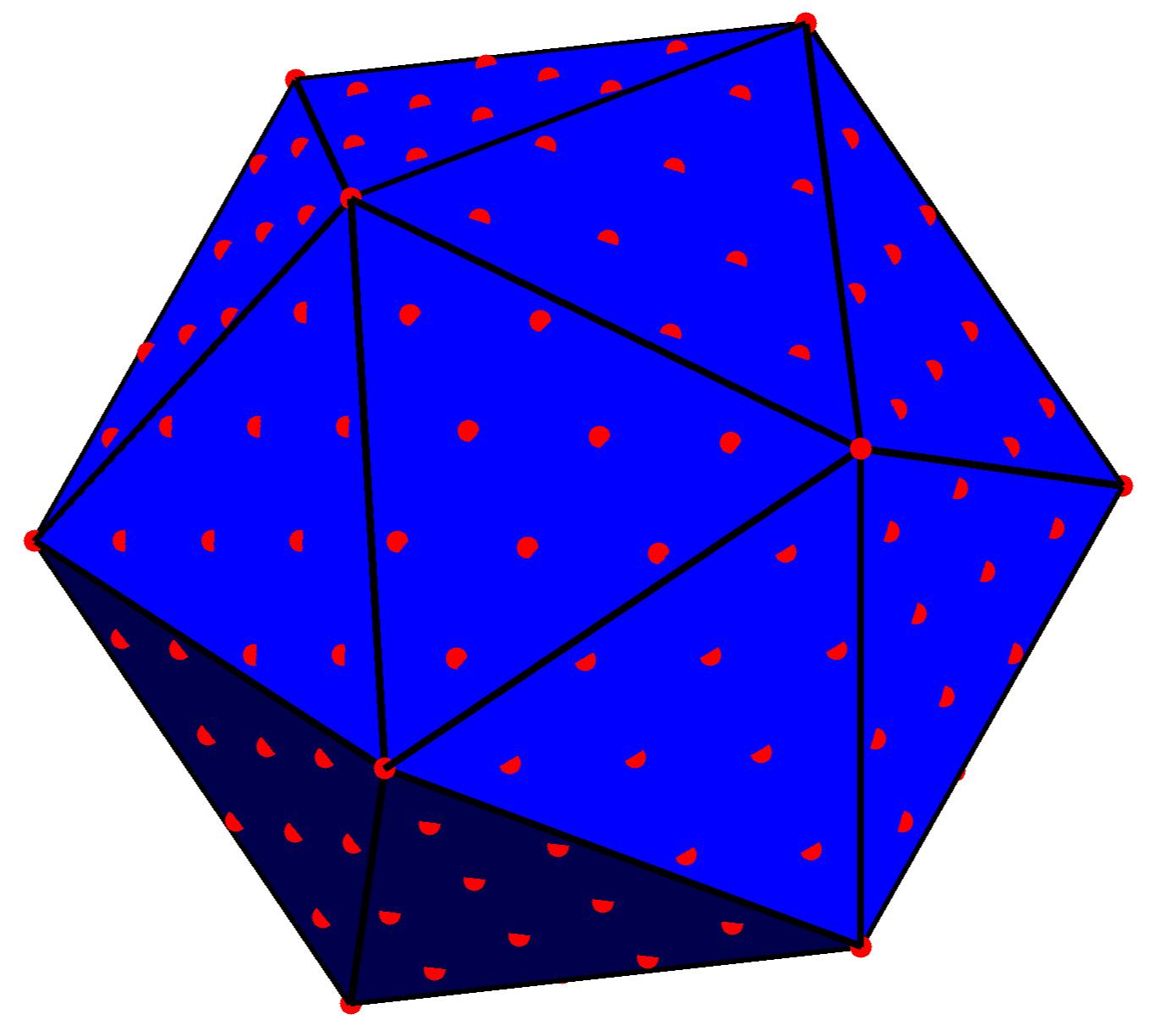
Рисунок 5.2 - Изображение точек треугольника на гранях икосаэдра

Выполним центральную проекцию полученного множества точек, лежащих на гранях икосаэдра, на поверхность сферы, (Рисунок 5.3).

Рисунок 5.3 - Центральная проекция точек икосаэдра на описанную сферу

Существенный недостаток данного метода – он не позволяет размещать произвольное количество точек. Это следует из свойств уравнения (1), которое относительно переменных m и n имеет решение не для всех значений N. В данном случае реализация метода решетки производилась при диаметре сферы D_сф = 0.5 м, заданного в условии, m = 2 и n = 3, подставив последние значения в уравнение (1) получим количество точек (элементов антенной решетки):

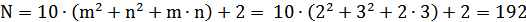
Так же к характеристикам реализованной сферы по данному алгоритму следует отнести полученные расстояния между парами соседних точек, обозначенных на рисунке 5.5. Соседней считалась пара, если она была связана ребром в триангуляционном графе по методу Делоне, (Рисунок 5.4) [10].

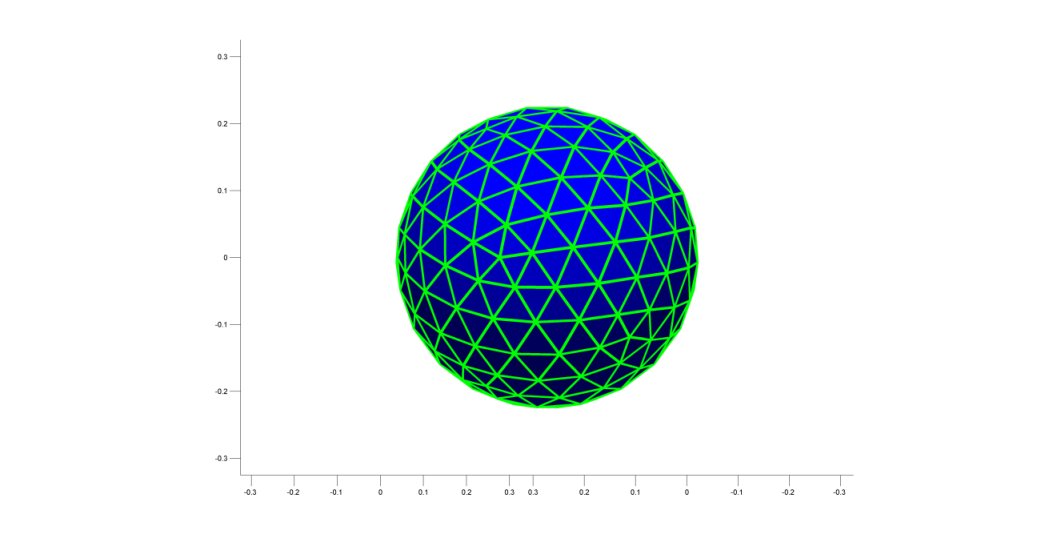
Рисунок 5.4 - Триангуляция Делоне

Рисунок 5.5 - Нормированная гистограмма расстояний между парами соседних точек

6 РАСЧЕТ ПАРАМЕТРОВ АНТЕННЫ

Расчет максимальной дальности действия при наименьшей мощности излучения по заданной рабочей частоте можно произвести по следующей формуле [11]:

где f₀ – рабочая частота антенного устройства.

Подставив значение рабочей частоты получим:

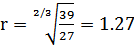км

Длина звуковой волны

,

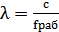(3)

где f – рабочая частота, с- скорость звука в среде.

Подставив значения в выражение (3) получи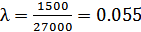м:

м

6.1. Длительность и период следования импульсов

Для получения минимальной мертвой зоны и наилучшей разрешающей способности по дистанции (глубине) используют как можно более короткие зондирующие импульсы. Его длительность можно вычислить по следующей формуле [4]:

,

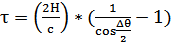(4)

где H – глубина ловли, H ≈ 1000 м;

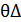– угол раствора основного лепестка ХН, 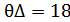^о ;

с – скорость звука в воде, 1500 м/c.

Подставляя известные данные в формулу (4) получим следующее значение длительности импульса:

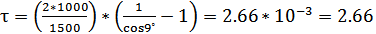мс

Период следования зондирующих импульсов 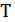выберем, исходя из условия:

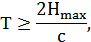
(5)

где 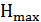– максимальная глубина;

с – скорость звука в воде.

Подставив известные значения в (5), получим:

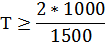
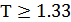сек

За период следования примем 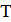= 2 секунды.

6.2. Коэффициент пространственного затухания

Пространственное затухание звуковой волны в водной среде происходит по причине расширения ее фронта и рассеяния энергии. Для частот, лежащих в диапазоне от 16 кГц до 60 кГц, можно применить следующую формулу для расчета коэффициента затухания:

,

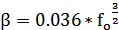(6)

где 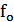- рабочая частота.

Подставляя известные значения в (6), получим:

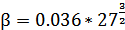
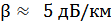
6.3. Резонансный размер преобразователя

Исходя из условия механического резонанса резонансный размер преобразователя можно рассчитать следующим образом:

,

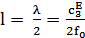(7)

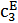- скорость звука в пьезокерамике ЦТС-24, ;

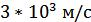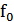– рабочая частота, 27 кГц.

Резонансный размер будет равен:

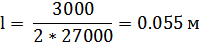
6.4. Акустическая мощность

Найдём полную излучаемую антенной акустическую мощность. Для этого воспользуемся формулой (8) [2]:

,

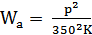(8)

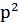– заданное в условии давление, развиваемое на расстоянии 1м, 200кПа;

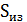– площадь излучающей поверхности;

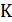– коэффициент осевой концентрации.

Минимальная величина коэффициента осевой концентрации – при крайних положениях ХН находится по формуле (9):

,

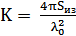(9)

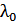– длина волны на рабочей частоте .

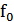Для нахождения площади излучающей поверхности воспользуемся:

,

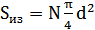N – количество преобразователей, N = 192;

d – диаметр круглой излучающей поверхности преобразователя, d = 0.03 м.

Таким образом можем получить:

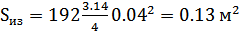
КОК будет равен:

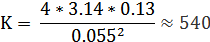
Акустическая мощность антенны следовательно будет:

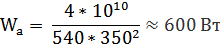
Мощность, излучаемая каждым преобразователем:

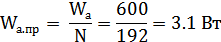
Удельная акустическая мощность:

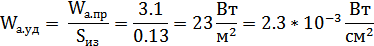
6.5. Допустимость удельной акустической мощности

Допустимость удельной акустической мощности по отношению к кавитационной прочности воды можно проверить в соответствии с графиком 1.a [2]. Работая в импульсном режиме при длительности импульса 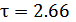мс, максимальная допустимая удельная акустическая мощность - до 10 Вт/см².

По условию величина заглубления антенного устройства H = 5 м, можем воспользоваться формулой (10) [3], которая дает возможность рассчитать порог кавитации на заданной глубине:

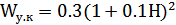
(10)

Подставив значения в вышеуказанную формулу, найдем порог кавитации:

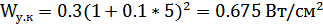
Таким образом, как видно из полученного результата, наше значение удельной акустической мощности на глубине 5 м полностью удовлетворяет условию.

Так же необходимо проверить допустимость удельной акустической мощности по отношению к механической прочности преобразователя. Подставив имеющееся значение удельной мощности в формулу (11), получим:

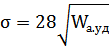
(11)

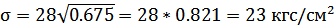
Значение удельной акустической мощности в 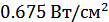также допустима и в этом случае, так как возникающие напряжения не превышают предела прочности керамики 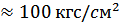и практически вчетверо меньше.

6.6. Необходимое возбуждающее напряжение

Для излучения требуемой акустической мощности необходимо определить возбуждающее напряжение. Произвести расчет можно, используя следующую формулу (12) [2]:

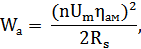
(12)

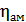- акустико-механический коэффициент полезного действия;

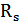- сопротивление излучения преобразователя;

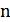– электромеханический коэффициент трансформации.

Выразим из вышеизложенной формулы возбуждающее напряжение:

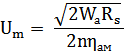
Акустико-механический коэффициент полезного действия 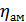определяют из экспериментальных данных, так как в настоящее время методики расчета этого коэффициента не разработано. Его значения лежат в диапазоне 0.6 - 0.8. Так как вероятнее всего в реальном воплощении наш преобразователь будет иметь потери в узлах креплений, а так же соприкасаться боковыми поверхностями с жидкостью или твердыми материала, то примем этот коэффициент равным 0.6.

Сопротивление излучение преобразователя можно рассчитать исходя из формулы (13):

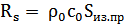
(13)

Подставляем значения и получаем:

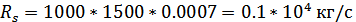
Коэффициент трансформации 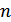будет рассчитываться из следующего уравнения (14) [2]:

,

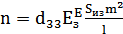(14)

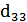– пьезоэлектрический модуль ЦТС-24, ;

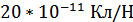m = 1 – количество секций преобразователя;

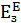– модуль Юнг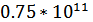а, Па.

После подстановки известных данных получим следующий результат:

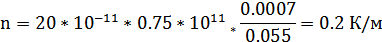
Таким образом теперь можем рассчитать напряжение возбуждения:

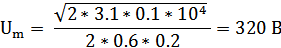
6.7. Определение сопротивлений

Сопротивление электрических потерь найдем из уравнения (15):

,

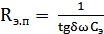(15)

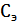– электрическая емкость;

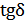– тангенс диэлектрических потерь, 0.04.

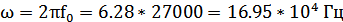
Определим электрическую емкость:

;

.

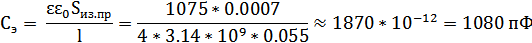
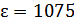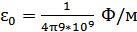Теперь можем найти сопротивление электрических потерь:

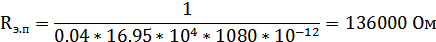
Рассчитаем механическое сопротивление преобразователя на резонансе:

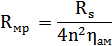
(16)

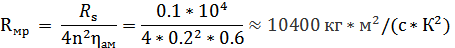
Далее, имея все данные, находим полное ваттное сопротивление по формуле (17):

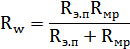
(17)

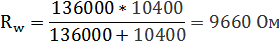
6.8. Определение коэффициента полезного действия

КПД является основным показателем эффективности проектируемого антенного устройства, и чем он больше, тем эффективнее антенна. Рассчитаем электроакустический КПД :

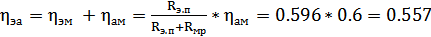
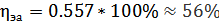
6.9. Полная электрическая мощность

Необходимая для питания всей антенны от генераторного устройства полная электрическая мощность будет равна:

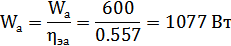
6.10. Чувствительность антенны

Чувствительность преобразователя в режиме холостого хода определим по формуле (18) [2]:

,

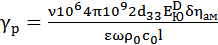(18)

– коэффициент дифракции;

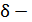расстояние между электродами, примем его по диаметру излучающего элемента, расположив электроды на торцевых поверхностях диаметрально,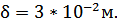

Коэффициент дифракции, который учитывает дифракцию акустической волны на приемной устройстве, выберем исходя из графика, приведенного в [2].

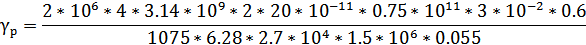
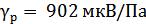
6.11. Добротность

Для преобразователя без накладок воспользуемся формулой определения добротности (19) [3]:

,

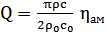(19)

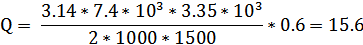
Полоса пропускания ПП: