Абсолютная энтропия и избыточность языка
| 2015_12_19 | |
| Работа Станкевич Анны, ФиПЛ в рамках курса «Вероятностные модели» |
| Проверка родства языков с помощью частотности символов и энтропии. На материале испанского и португальского изданий книги Дж.К.Роулинг «Гарри Поттер и философский камень» |
Оглавление
Ключевые слова. 3
Гипотеза. 3
Аннотация. 3
Понятие энтропии. 4
Абсолютная энтропия и избыточность языка. 4
Исследовательский корпус и возможная погрешность. 5
Вычисление энтропии. 6
Вывод. 8
Приложения и рассчеты.. 9
Список литературы: 9
Ключевые слова: математическая статистика и лингвистика, энтропия
Гипотеза
При проверке родства языков возможно использовать статистический анализ текста не только в семантике и грамматике, но и в символьном составе текстов. Предполагается, что у близкородственных языков будет близкая частотность символов и их энтропия.
Задачи
1. Статистический анализ текста
2. Рассмотрение графических и фонетических особенностей языка
3. Подсчет абсолютной и относительной частотности символов
4. Подсчет энтропии
Аннотация
Язык сводится к серии символов, которые считаются и анализируются как последовательность повторения секвенций.
В настоящей работе рассчитана энтропия художественного текста. Расчёт энтропии выполнен на основе переводов книги о Гарри Поттере, а именно 293028 литер испанского языка и 382227 португальского языка. Для анализа проведен анализ классических, основных алфавитов языков, а также анализ реально используемого «алфавита» отражающего некоторые фонетические особенности данных языков с помощью буквосочетаний и диакритик.
Понятие энтропии
Энтропия – это понятие, использующееся в термодинамике, которое вошло в теорию информации, чтобы обозначить уровень дезинтеграций в процессе информации. Согласно основному уравнению Шеннона-Вивера, количество информации какой-нибудь системы является альтернативой
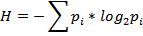
т.е. оно тождественно сумме вероятностей появлений каждой из возможных альтернатив.
Энтропия всегда обратно пропорциональна вероятности результата. Она максимальна, когда все вероятности в совокупности одинаковы, т. е. когда совокупность наименее упорядочена, а она минимальна и равна нулю, когда одна из вероятностей имеет числовое значение 1 и когда остальные равны нулю.
Абсолютная энтропия и избыточность языка
Это величина, равная максимуму информации, которую можно передать единицей данного языка. В теории информации обычно под единицей языка понимают один символ (букву) соответствующего алфавита, а абсолютная энтропия вычисляется при условии равновероятности всех последовательностей символов.
Если в алфавите языка используется L различных букв, то абсолютная энтропия языка (бит на букву) можно вычислить как:
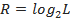
Величина избыточности разных языков мира колеблется в пределах 70-80%. Во всех языках на всех уровнях присутствуют избыточные элементы. Избыточность в языке неслучайна: её функция — облегчить коммуникацию при неблагоприятных условиях передачи информации. Избыточность представляет собой систему предупреждения возможных ошибок.
Абсолютная энтропия для португальского и испанского языков:
| 4,754888 | Абсолютная энтропия основного алфавита | |
| 5,584963 | Энтропия алфавита с различением буквосочетаний, знаков с диакритиками и букв основного алфавита | |
Таблица-1. Португальский
| 4,807355 | Абсолютная энтропия основного алфавита | |
| 5,169925 | Абсолютная энтропия алфавита с различением буквосочетаний, знаков с диакритиками и букв основного алфавита | |
Таблица-2. Испанский.
Исследовательский корпус и возможная погрешность
Исследования данной работы проводились на материале переводов с английского на испанский и португальский языки книги «Гарри Поттер и философский камень» Джоан К. Роулинг. Частота появления символов в корпусе была выявлена с помощью поиска по тексту. Для каждого языка проведено исследование официального алфавита и алфавита, отражающего фонетические особенности. С алфавитами можно ознакомиться ниже.
Черным цветом выделены основные буквы алфавитов, серым – буквы, встречающиеся лишь в заимствованных словах, красным – буквосочетания и диакритики имеющие особое звучание/сферу употребления.
Рисуснок-1 – португальский.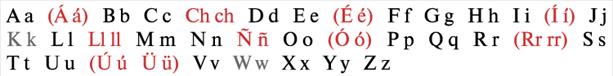 
Рисунок-2 – испанский.
Т.к. книга, на которой было проведено исследование, является переводом с английского языка, возникает ряд проблем:
1. Повышается вероятность использования заимствованных букв. В именах и названиях. Особенно в португальском, где предпочитают не транслитерировать англоязычный текст.
2. Небольшую погрешность вносят выдуманные слова, а также заклинания с латинскими корнями.
Вычисление энтропии
Учитывая, что погрешность при вычислении абсолютной энтропии достаточно велика, используется вычисление энтропии с помощью относительной частоты символа в тексте. С помощью статистического анализа текстов получены данные об относительной частотности появление каждого символа.
Таблица-3 – португальский Таблица-4 – испанский
| Буква | Относительная | Буква | Относительная частота | ||
| A(Á, À, Â, Ã) | 0,134261 | A (À) | 0,154991 | ||
| A | 0,122948 | A | 0,149886 | ||
| Á | 0,003427 | Á | 0,005104 | ||
| À | 0,000764 | B | 0,022311 | ||
| Â | 0,000157 | C | 0,041234 | ||
| Ã | 0,006964 | C (исключая ch) | 0,032772 | ||
| B | 0,010101 | Ch | 0,004013 | ||
| C | 0,029632 | F | 0,008462 | ||
| C (исключая ch) | 0,026911 | G | 0,017783 | ||
| Ç | 0,003043 | H | 0,01663 | ||
| Ch | 0,002721 | I(Í) | 0,068483 | ||
| D | 0,043456 | I | 0,057769 | ||
| E (È, É, Ê) | 0,117067 | Í | 0,010714 | ||
| E | 0,111049 | J | 0,007302 | ||
| È | 0 | K | 0,000293 | ||
| É | 0,00337 | L | 0,060301 | ||
| Ê | 0,002648 | L (исключая lh, ll) | 0,054367 | ||
| F | 0,009866 | Ll | 0,00591 | ||
| G | 0,012676 | Lh | 2,39E-05 | ||
| H | 0,01676 | M | 0,030892 | ||
| I(Ì, Í, Ï) | 0,049863 | N | 0,08108 | ||
| I | 0,048479 | N (исключая nh, Ñ) | 0,078476 | ||
| Ì | 0 | Nh | 1,71E-05 | ||
| Í | 0,001384 | Ñ | 0,002586 | ||
| Ï | 0 | O (Ó) | 0,121369 | ||
| J | 0,002268 | O | 0,110314 | ||
| K | 0,000154 | Ó | 0,011055 | ||
| L | 0,026942 | P | 0,030991 | ||
| L (исключая lh) | 0,023803 | Q | 0,014955 | ||
| Lh | 0,003139 | R | 0,079271 | ||
| M | 0,041572 | Rr | 0,007032 | ||
| N | 0,046899 | S | 0,081564 | ||
| N (исключая nh) | 0,042783 | T | 0,050109 | ||
| Nh | 0,004115 | U (Ú, Ü) | 0,066609 | ||
| O (Ò, Ó, Ô, Õ) | 0,100453 | U | 0,051586 | ||
| O | 0,098591 | Ú | 0,001474 | ||
| Ò | 0 | Ü | 3,41E-06 | ||
| Ó | 0,001363 | V | 0,013549 | ||
| Ô | 0,000207 | W | 0,000945 | ||
| Õ | 0,000293 | X | 0,000935 | ||
| P | 0,02503 | Y | 0,017811 | ||
| Q | 0,011744 | Z | 0,005098 | ||
| R | 0,068765 | ||||
| R (исключая rr) | 0,062594 | ||||
| Rr | 0,006172 | ||||
| S | 0,067052 | ||||
| T | 0,038197 | ||||
| U (Ù, Ú, Û) | 0,045551 | ||||
| U | 0,044814 | ||||
| Ù | 0 | ||||
| Ú | 0,000738 | ||||
| Û | 0 | ||||
| V | 0,017576 | ||||
| W | 0,000531 | ||||
| X | 0,002483 | ||||
| Y | 0,005212 | ||||
| Z | 0,004081 | ||||
При подсчете энтропии по формуле, описанной выше, получаем:
Таблица-6 – португальский
| 4,216141 | Энтропия основного алфавита | |
| 5,197892 | Энтропия алфавита с различением буквосочетаний, знаков с диакритиками и букв основного алфавита | |
Таблица-7 - испанский
| 3,996881 | Энтропия основного алфавита |
| 5,244257 | Энтропия алфавита с различением буквосочетаний, знаков с диакритиками и букв основного алфавита |
|
| |
|
|
Вывод
Частотность отдельных символов позволяет использовать данный математическо-статистический метод для подтверждения родства языков. Для более точного анализа следует проследить графико-фонетическую миграцию символов в каждом отдельном языке. Кроме того, следует отметить, что в данной работе точность исследования уменьшается т.к. в силу того, что анализируется современный текст, не взяты исторически присутствовавшие символы (такие как Ç в испанском, к примеру).
Приложения и рассчеты
Для португальского языка: Португальский.xlsx
Для испанского языка: Испанский.xlsx
Список литературы:
1. Пиперски А.Ч. 2015. Алгоритм Хаффмана и Энтропия, c.12
2. Вукчевич З. 2012. Энтропия сербохорватского языка: исследование на опусе П.П.Негоша.
3. http://book.itep.ru/10/shennon.htm
4. http://www.paratype.ru/help/language/language1.asp?langCode=71