5, Понятие поверхности равного давления. Уравнение поверхности равного давления. Вывод уравнения равного давления.

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

БИЛЕТ 21

27. Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре.

Малым называется отверстие, вертикальный размер которого значительно (в 10 и более раз) меньше напора перед отверстием, что во всех точках этого отверстия практически одинаковым.

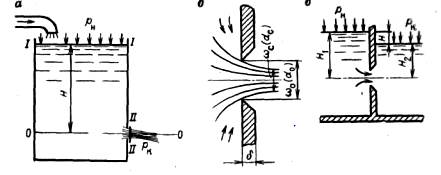
При истечении жидкости через малое отверстие площадью w₀ в тонкой стенке (d £ 0,2 d₀) в результате инерции частиц, они движутся по криволинейным траекториям (б).

На небольшом расстоянии от отверстия (для круглого = ~ половине его диаметра) образуется сжатое сечение, имеющее min площадь w_с и практически параллельноструйное движение частиц.

Обозначим 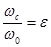- коэффициент сжатия струи.

Для отверстий круглой и квадратной формы e = 0,6 ¸ 0,64

Чтобы определить скорость u₁ истечения и расход Q жидкости через малое отверстие в тонкой боковой стенке резервуара (а) при постоянном уровне жидкости в резервуаре H = const, т.е. когда через отверстие имеет место установившиеся движение жидкости.

Проведем два сечения: I-I – по пов-сти жидкости в резервуаре.

II-II – по струе (в сжатом ее сечении) и плоскость сравнения 0-0.

Затем ур-ние Бернулли для этих сечений:

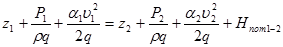
Пусть давление окружающей среды на резервуар P_H, а на выходе – P_k, тогда P₁ = P_H; P₂ = P_к(в том случае, когда истечение струи происходит в атмосферу в любом сечении струи давления P_a).

В связи с большим поперечным сечением резервуара скоростью в нем можно пренебречь, поэтому u₁ » 0 и потери напора на трение о стенки резервуара Н_Дл » 0, тогда

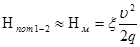где Н_м – местные потери напора

x - коэффициент местного сопротивления (отверстия)

Обозначим u₂через u - скорость истечения через отверстие.

Тогда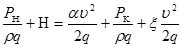

H = z₁ (высота от пл-ти равнения до свободной пов-сти)

Найдем отсюда скорость u:

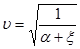
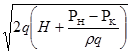(1)

Обозначим: 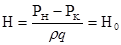- приведенный напор перед отверстием.

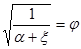- коэффициент скорости.

Тогда 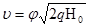(2)

Если пренебречь гидравлическим сопротивлением и неравномерностью распределения скоростей по струе, т.е. принять x = 0; a = 1, что характерно для идеальной жидкости, то j = 1 и получим известную формулу Торричелли:

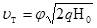(3) (теоретическая)

Вследствие того, что j < 1, действительная скорость истечения u будет всегда меньше теоретической u_Т. при истечении воды и воздуха, когда имеет место турбулентное движение, можно принимать:

j » 0,97 ¸ 0,98 и x » 0,06

Расход жидкости через отверстие будет равен:

Q = uw_c

Заменим, что w_c = ew₀, а u - из ур-ния (2)

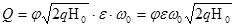
Или m = je - коэффициент расхода отверстия.

При значениях j и e значение m = 0,60 ¸ 0,63 - для отверстий круглой и квадратной формы.

Эти значения:

j = 0,97 ¸ 0,98 имеют место при больших числах Рейнольдса (10^{5 и более)}

e = 0,6 ¸ 0,64

m = 0,6 ¸ 0,63

Если пространство, куда вытекает жидкость, заполнено жидкостью (рис. в), то такое истечение называется истечением под уровень или истечением через затопленное отверстие. Принимая, как и в предыдущем случае, что давление на поверхности жидкости в резервуарах равны P_H и P_K, а расстояния от поверхностей до отверстия – Н₁ и Н₂.

Составляя ур-ние Бернулли получим для определения u и Q, только Н₀ будет равно 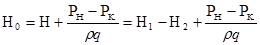(приведенный напор)

Коэффициенты j; e; m для малого затопленного отверстия в тонкой стенке практически будут такими же, как для не затопленного.

10. Виды движения жидкости

Существует два вида движения: установившееся и неустановившиеся.

1) Если основные параметры движения жидкости зависят от времени, то движение будет неустановившееся.

2) Если параметры движения жидкости не зависят от времени, то движение наз. установившемся.

Пример неустановившегося:

Движение – истечение жидкости из резервуара при переменном ее уровне (опоражнивание резервуара).

Примером неустановившегося движения является истечение жидкости из резервуара при постоянном уровне – приток равен расходу.

Установившиеся движение – основной вид движения для гидравлических расчетов, поэтому в данном курсе будут изучаться закономерности изменения параметров при этом движении жидкости.

В зависимости от хар-ра изменения скорости по длине потока движение может быть:

1. Равномерное u = const

2. Неравномерное – скорость изменяется по величине и направлению

3. Плавно изменяющиеся – изменение скорости происходит плавно.

Вихревое движение.

Движению частиц часто сопутствуют вихревое движение (оно вызвано вращением элементарного объема). Угловая скорость вращения w элементарного объема жидкости наз. вихрем, а линия, касательная к векторам вихря – вихревой линией.

Пов-сть, образованная вихревыми линиями наз. вихревой трубкой. Жидкость, заключенная внутри вихревой трубки – вихревая нить – шнур.

В поступательном движении существуют понятия:

Линия тока – линия в каждой точке, которой в данный момент времени вектор скорости жидкости совпадает с касательной к этой линии. В установившемся движении линии тока является траекторией частицы жидкости.

Трубка тока – поверхность, образованная линиями тока, проведенными в данный момент времени через все точки бесконечно малого замкнутого контура.

5, Понятие поверхности равного давления. Уравнение поверхности равного давления. Вывод уравнения равного давления.

Из ур-ния(2) можно получить ур-ние поверхности равного давления.

Поверхность равного давления – пов-сть, давление во всех точках которой одинаково. (p = const)

Уравнение такой пов-сти:

dp = r (xdx + ydy + zdz)

Предложение: при p = const; dp = 0, т.к. r ¹ 0

Тогда r (xdx + ydy + zdz) = 0

Следовательно, xdx + ydy + zdz = 0 (2)

Таким образом: все частицы жидкости, расположенные на пов-сти равного давления, обладают одинаковой удельной потенциальной энергией, соответствующей массовым силам.

Одной из пов-стей равного давления является свободная пов-сть жидкости, т.е. поверхность жидкости, граничащая с газовой средой, т.к. во всех ее точках давление равно внешнему давлению p₀.

Уравнение пов-сти равного давлений можно рассматривать как ур-ние работы массовых сил при элементарном перемещении по поверхности равного давления. Из равенства нулю этой работы следует:

Ускорение массовых сил, действующих на жидкость, находящегося в относительном покое, в любой точке жидкости направлено по нормам к пов-сти равного давления, проходящей через эту точку.

Массовые силы, действующие на единицу массы жидкости (т.е. точку) равны:

M = m × a (разделим на m), получим

M = a – равнодействующая массовых сил равна и пропорциональна ускорению массовых сил.

·) Жидкость находится в равновесии в резервуаре в поле действия только силы тяжести.

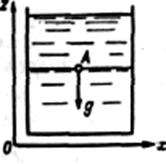
В этом случае проекции результирующей единичных массовых будут:

x = 0; y = 0; z = -q = 0

Подставляя это значение в ур-ние (2) получим: -qdz = 0, после интегрирования получим:

qz = const

Это ур-ние горизонтальной плоскости. Следовательно, в покоящейся однородной жидкости (p = const) любая горизонтальная плоскость является плоскостью равного давления.

БИЛЕТ 22

8. Вывод формулы для силы давления жидкости на плоскую стенку.

Чтобы определить силу давления на плоскую стенку, возьмем наклонную стенку и выделим на плоской боковой стенке сосуда, наклонной в общем случае к горизонту под углом a, произвольную фигуру площадью F.

Определим действующую на нее со стороны жидкости силу давления P.

Для наглядности совместим рассматриваемую стенку с плоскостью чертежа (т.е. повернем ее на угол 90 ° вокруг оси y).

Так как давление жидкости в различных по высоте точках площади F разное, то выделим на этой площади элементарную площадку, находящуюся на расстоянии h от свободной пов-сти жидкости или 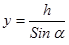от оси x; h = y Sin a.

Для такой бесконечно малой площадки давление во всех ее точках одинаково и равно:

P = rqh = rq y Sin a

Следовательно, сила давления жидкости на элементарную площадку будет:

dp = pdF = rq y Sin dF

Сила давления на всю рассматриваемую площадь F:

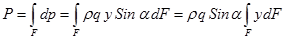
выражение 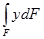- S_x статический момент рассматриваемой площади относительно оси x, который равен произведению площади этой фигуры F на расстояние от ее центра тяжести до оси x, т.е. y_c × F.

Т.о. P = rq Sin a × y_c × F или заменяя y_c Sin a = h_c

P = rq h_c × F = P_c × F

Получим:

(1)

P_с = rq h_c

Из уравнения (1) видно, что сила давления жидкости на плоскую стенку P равна произведению смоченной жидкостью площади стенки F на гидростатическое давление в ее центре тяжести:

2) Если на свободную поверхность жидкости действует давление, отличное от атмосферного, то силу давления на стенку найти по формулам:

P = (rq h_c + P_M) × F = (P_с + P_M) F

P = (rq h_c - P_b) × F = (P_с-P_b) F,

где P_M и P_b – манометрическое давление и вакуум на свободной поверхности.

В ряде случаев, кроме значения силы давления жидкости на стенку, необходимо знать координаты точки ее приложения – центра давления.

Предположим, что сила давления P приложена в т.D, находящейся на расстоянии y_D от оси x. В соответствии с теоремой Вариньона о моменте равнодействующей (момент равнодействующей силы относительно какой-либо оси равен сумме моментов составляющих сил относительно той же оси).

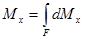или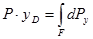

Заменив в последнем выражении P и dP их значениями, получим: dP = Pd F

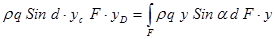
Вынесем постоянные за знак интеграла и сократим их с аналогичными величинами в левой части ур-ния:

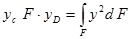
Выражение 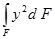представляет собой момент инерции площади фигуры относительно оси x – Y_x, который может быть выражен через момент инерции Y_с относительно центральной оси, êê оси x, следующим образом

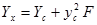
Тогда: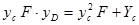

Откуда: 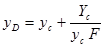(2)

Из ур-ния (2) видно, что центр давления для плоской стенки находится всегда ниже ее центра тяжести, т.к. 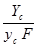> 0.

Горизонтальная координата центра давления x_D находится на оси симметрии площади фигуры.

В частом случае, когда a = 0, т.е. для горизонтального дна сосуда, расположение от свободной пов-сти до центра тяжести площади h_c будет равно высоте жидкости в сосуде H, поэтому сила давления жидкости на дно сосуда:

P = rq H F

Из этого выражения видно, что различные по форме сосуда, имеющие одинаковые площади доньев и затопленные одинаковой жидкостью на одну и туже высоту, будут иметь одинаковую силу давления на дно независимо от формы сосуда и количества находящейся в нем жидкости (гидростатический парадокс).

r₁ =r₂ = r₃

Из ур-ния P = rqh F при h = const, видно, что P₁ = P₂ = P₃, независимо от формы сосуда и количества находящейся в них жидкостей.

13. Уравнение неразрывности

Ур-ние неразрывности (сплошности) является математическим выражение закона сохранения массы в гидромеханике.

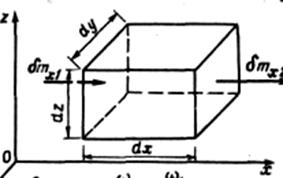В движущейся жидкости выделим параллелепипед объема dV с бесконечно малыми ребрами dx, dy, dz.

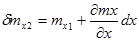
За время dt в него входит масса m₁ и выходит m₂, приращение массы в направлении оси OX.

Dm_x = dm_x₁ – dm_x₂

где dm_x₁ = r_x × U_x dy dz dt

dm_x2 = r_x × U_x dy dz dt + 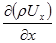dx dy dz dt

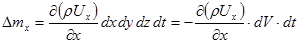
по аналогии

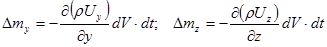
приращение массы в параллелепипеде

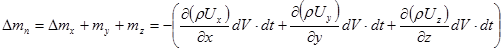(1)

Изменение массы в объеме dV за время dt может быть только за счет изменения плотности, следовательно

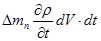(2)

Приравняв выражения (1 и 2) получим:

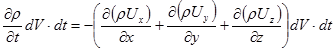
после преобразования и сокращение получим уравнение неразрывности в форме Эйлера:

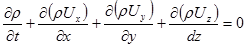
Для установившегося движения 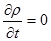, тогда уравнение примет вид:

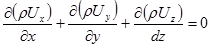
Если жидкость несжимаемая, то r = const и ур-ние неразрывности будет

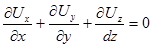
21. Закономерности ламинарного режима движения жидкости

Ламинарный режим движения жидкости хар-ся параллельным струйным упорядоченным движением частиц жидкости.

Закон распределения скоростей по сечению.

Для установления закона распределения скоростей по сечению при ламинарном движении рассмотрим поток жидкости в горизонтальной круглой трубе радиусом r, находящейся в установившемся равномерном движения.

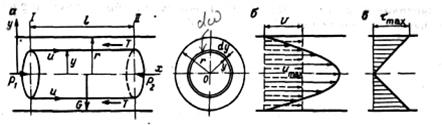
Выделим в этом потоке вокруг его оси объем жидкости виде цилиндра длиной 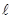и радиусом y и спроектируем все действующие на него силы на ось потока. При установившемся равномерном движении сумма проекции этих сил равна 0.

DP_x – T_x – G_x = 0

DP_x = P_x₁ – P_x₂

где DP_x – проекция равнодействующей сил давления на торцевые пов-сти цилиндра, направленной в сторону движения.

T_x – проекция силы трения, действующей на боковую пов-сть цилиндра и направленной в сторону, противоположную движению.

G_x – проекция силы тяжести

Т.к. линия действия DP и T параллельны, а G ^ оси потока, то

DP_x = DP; T_x = T; G_x = 0,

поэтому DP = T (1)

Как видно из рисунка DP = P₁ – P₂ = (P₁ – P₂) py²,

где P₁ и P₂ – давление в сечениях I-I и II-II, заменив (P₁ – P₂) его значение rq 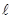i

получим: DP = rq 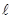ipy² (2)

В соответствии с уравнением

m = ¶r

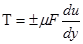
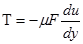
где m - динамическая вязкость жидкости, которая определяется ¶ = m/r;

F = 2py 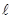– боковая пов-сть цилиндра.

Знак (-) принят потому, что с увеличением расстояния от оси потока скорость частиц жидкости (U) уменьшается. Следовательно:

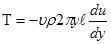(3)

Подставим значения DP и T из ур-ний (2 и 3) в ур-ние (1)

Получим:

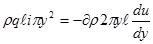
Сделаем преобразование и получим:

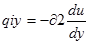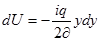
Проинтегрируем:

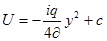(4)

Для определения постоянной интегрирования C задаемся начальными условиями: при y = r, т.е. стенки трубы, вследствие прилипания частиц жидкости U = 0, тогда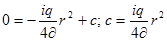

Подставим значение C в ур-ние (4), получим закон распределения скоростей по сечению круглой трубы при ламинарном режиме движения, установленный английским ученым Стоксом.

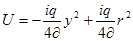
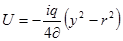(5)

При y = 0 на оси трубы U = U_max

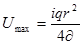
Т.к. это уравнение параболоида вращения с вершиной, лежащей на оси трубы, то при ламинарном движении эпюра скоростей по сечению будет иметь форму квадратичной параболы.

Подставим в ур-ние 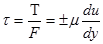значение 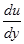, установим закон распределения касательных напряжений вдоль радиуса:

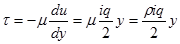(6)

из этого ур-ния видно, что при ламинарном режиме движения изменения t вдоль радиуса происходит по линейному закону, причем t_max = 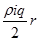будет при y = r, т.е. у стенки трубы; t_max = 0 будет при y = 0, т.е. на оси трубы.