Выбор основной системы.
Основная система получается из заданной статически неопределимой системы путем исключения лишних внешних и внутренних связей.
Во всех случаях основная система должна быть геометрически неизменяемой, неподвижной и статически определимой.
«Основная система»
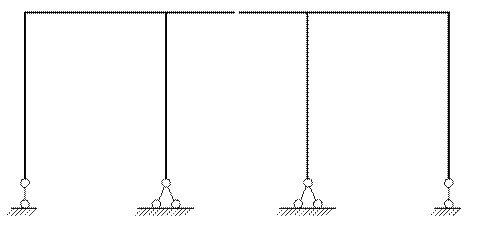
«Эквивалентная система»
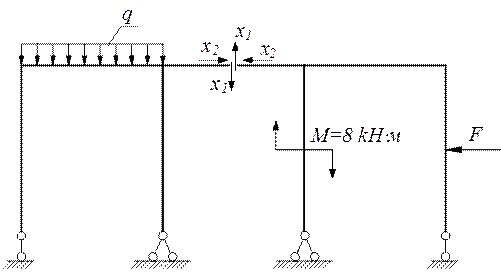
Составление канонических уравнений.
В заданной системе в направлениях имеющихся связей, в том числе и тех, которые отброшены при переходе к эквивалентной системе, перемещений быть не может, поэтому в эквивалентной системе по направлениям отброшенных связей X1 и X2 перемещения должны быть равны нулю. Следовательно реакции отброшенных связей X1 и X2 должны иметь такие значения, при которых перемещения по их направлениям в эквивалентной системе отсутствуют.
Аналитически это условие записывается в виде канонических уравнений:
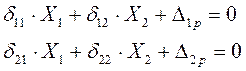
В системе канонических уравнений в качестве коэффициентов при неизвестных X 1 и X 2 стоят перемещения основной системы вызываемые единичными силами или моментами, действующими по направлению отброшенных связей.
Первые индексы перемещений определяют, в направлении какой силы происходит перемещение, вторые указывают какой силой вызвано данное перемещение, т.е.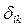 
- перемещение по направлению х i от действия х k=1 в основной системе.
Свободные члены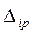 
определяют перемещения, вызванные действием заданной нагрузки /q, p, m/ по направлению х i.
Определение коэффициентов при неизвестных и свободных членах
Коэффициенты 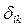и свободные члены 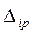как перемещения при изгибе в общем случае можно определить с помощью формулы Мора – Максвелла /интеграл Мора/:
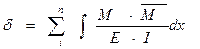
где M – изгибающий момент в произвольном сечении х от заданной
нагрузки, вызывающей перемещение;
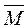- изгибающий момент в том же сечении х от единичной силы, соответствующей определенному перемещению.
Так как единичная эпюра изгибающих моментов 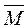всегда прямолинейна, то для вычисления интеграла Мора целесообразно пользоваться способом Верещагина.
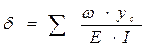
где ω – площадь эпюры М (изгибающий момент от заданно нагрузки);