>Симметрия щодо площині
Нехай a - довільна фіксована площину. З точки X постаті опускаємо перпендикулярXA на площину a і вкриваю його продовженні за точкуAоткладиваем відрізокAX', рівнийXA. Крапка X' називається симетричній точці X щодо площині a, а перетворення, яке переводить XX стсимметричную їй точку X', називається перетворенням симетрії щодо площині a.
Якщо точка X у площині a, то вважається, що вищу точку X перетворюється на себе. Якщо перетворення симетрії щодо площині a переводить постать у себе, то постать називається симетричній щодо площині a, а площину a називається площиною симетрії цієї фігури.
Поворот
Поворот площині близько даної точки називається такий рух, коли кожен промінь, що виходить із точки, повертається однією і хоча б кут щодо одного й тому самому напрямі.
Це означає, що й при поворот близько точкиO точка перетворюється на точку X', то променіOX іOX' утворюють і той ж кут, як і вона була точка X. Цей кут називається кутом повороту. Перетворення постатей при повороті площині також називається поворотом.
Паралельний перенесення у просторі
Паралельним перенесенням у просторі називається таке перетворення, у якому довільна точка (x; y;z) постаті перетворюється на точку (>x+a;y+b;z+c), де числаa,b,c одні й самі всім точок (x; y;z). Паралельний переносів просторі задається формулами
x'=x+a,y'=y+b,z'=z+c,
виражають координати x', y',z' точки, у якому переходить точка (x; y;z) при паралельному перенесення. Також, як і площині, доводяться такі властивості паралельного перенесення:
1.Параллельние перенесення є рух.
2. При паралельному перенесення точки зміщуються по паралельним (чи співпадаючим) прямим одне і те відстань.
3. При паралельному перенесення кожна пряма перетворюється на паралельну їй пряму (чи себе).
4. Хоч би якими були точки A і A', існує єдиний паралельний перенесення, у якому точка A перетворюється на точку A'.
Новим для паралельного перенесення у просторі є що властивість:
5. При паралельному перенесення у просторі кожна площину переходить або у себе, або у паралельну її площину.
Справді, нехай a - довільна площину, проведемо у цій площині дві пересічні прямі a і b. При паралельному перенесення прямі a і b переходять або у себе, або у паралельні прямі a' і b'.Плоскость a перетворюється на деяку площину a', яка стелиться через прямі a' і b'. Якщо площину a' не збігаються з a, то теоремі про поїздку двох від перетинання прямих площині відповідно паралельними з пересічними прямими іншій площині, вона паралельна a, що потрібно було довести.
25. Перетворення подібності площині. Гомотетія площині
Визначення. Хай є дві прямокутній декартовій системі координат Oij і O / i / j /, при цьому | i / | = | j / | = k | i | = k | j | = k (k> 0). Тоді перетворення площині, яке кожної точки М з координатами (x, y) щодо O / i / j / ставить відповідно точку М 'з тими ж координатами (x, y), але відносно Oij, називається перетворенням подібності площині з коефіцієнтом подібності k .
З визначення випливає, що тотожне перетворення і рух є перетвореннями подібності.
Основна властивість перетворення подібності.
Перетворення подібності площині змінює відстань між будь-якими двома точками площини в одному і тому ж відношенні, що дорівнює коефіцієнту подібності k, тобто для будь-яких точок М, N і їх образів М ', N' виконується рівність | M / N / | = k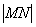 
.
Доказ. Нехай щодо Oij точки М і N мають координати: М (x 1, y 1), N (x 2, y 2). Тоді =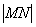 
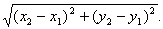
Образи М 'і N' точок М, N мають відповідно ті ж координати (x 1, y 1), (x 2, y 2) щодо системи координат O / i / j /. Знайдемо:
= = 
= 
= 
= 
= 
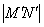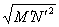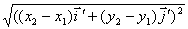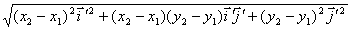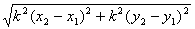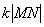, Так як 
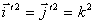і 
.
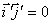Властивості перетворення подібності.
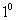Перетворення подібності площині всяку пряму відображає в пряму.
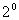Перетворення подібності площині відображає полуплоскость з кордоном 
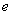в полуплоскость з кордоном 
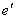де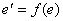 
.
Перетворення подібності площині зберігає просте відношення трьох точок прямої.
Перетворення подібності площині зберігає відношення "лежати між".
Перетворення подібності площині відображає кут у рівний йому кут.
Перетворення подібності площині відображає відрізок у відрізок, промінь в промінь.
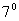Перетворення подібності площині відображає паралельні прямі в паралельні прямі.
Слідство. Перетворення подібності площині відображає паралелограм в паралелограм.
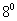Перетворення подібності площині відображає вектор в вектор, суму векторів в суму векторів і добуток кількості на вектор у твір того ж числа навідповідний вектор.
Теорема. Якщо перетворення подібності f з коефіцієнтом подібності k задано двома системами координат Oij і O / i / j /, при цьому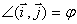 
і O / (x 0, y 0), то координати будь-якої точки M (x, y) Oij і її образу M / (x /, y /) O / i / j / пов'язані співвідношеннями:
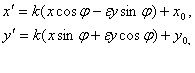де 
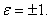(1)
Доказ спирається на визначення перетворення подібності, на формули, що зв'язують координати однієї і тієї ж точки щодо двох прямокутних декартових систем координат, на розкладання вектора по базисами.
Зауваження. При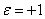 
системи координат Oij і O / i / j / однаково орієнтовані, а при 
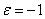протилежний орієнтовані.
Визначення. Перетворення подібності площині, визначається формулами (1) називається перетворенням подібності першого роду при 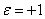і перетворенням подібності другого роду при .
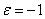З основного властивості перетворення подібності і вірного твердження, зворотного йому (якщо перетворення площині змінює відстань між точками в одному і тому ж відношенні, що дорівнює k> 0, то воно є перетворенням подібності з коефіцієнтом подібності k), слід інше визначення перетворення подібності.Визначення. перетворенням подібності площині з коефіцієнтом подібності k> 0 називається перетворення площини, що змінює відстань між будь-якими точками в одному і тому ж відношенні, що дорівнює k.
Гомотетія площині.
Визначення. Гомотетія площині з центром гомотетии О і коефіцієнтом гомотетии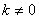 
називається перетворенням площині, яке будь-якої точці М площини ставить відповідно точку М / за законом
.
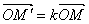Позначення. 
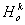- Гомотетія площині з центром гомотетии О і коефіцієнтом гомотетии k.
Визначення. Гомотетічнимі називаються фігури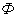 
і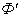 
= 
.
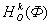1) Гомотетічние точки М і М / лежать на одній прямій з центром гомотетии Про.
2) Точки М і М / лежать по один бік від центру О, якщо k> 0, і - по різні сторони, якщо k <0.
3) М / N / = | k | MN.
4) Гомотетія площині є при:
k = 1-тотожним перетворенням;
k =- 1-центральної симетрією.
Формули гомотетии з центром у початку координат:
, 
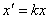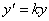
Якщо центр гомотетии має координати S (x 0, y 0), то формули гомотетии з центром S мають вигляд:
, 
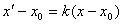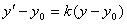
Якщо введемо позначення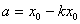 
, 
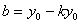то отримаємо формули
, 
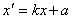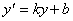
Основна властивість гомотетии.
Для будь-яких точок М, N і їх образів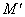 
, 
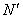має місце рівність:
.
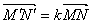Доказ. Скористаємося равенствами:
, 
, , 
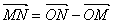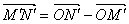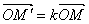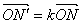і знайдемо
.
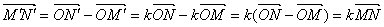Слідства.
1) Гомотетія з коефіцієнтом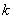 
є перетворенням подібності з коефіцієнтом подібності 
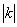, Так як з основного властивості слід 
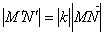або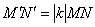 
.
2) 
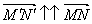, Якщо k> 0, і 
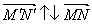, Якщо k <0.
3) Гомотетія площині має всі властивості перетворення подібності, зокрема: пряму відображає в пряму, паралельні прямі - у паралельні прямі, Змінює всі відстані в одному і тому ж відношенні, зберігає кути.
Характерні властивості гомотетии.
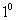Гомотетія площині має одну нерухому точку - центр гомотетии.
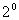Гомотетія площині відображає пряму, що проходить через центр гомотетии, в себе.
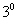Гомотетія площині ( 
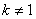) Відображає пряму, в паралельну їй пряму, так не проходить через центр гомотетии.
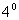Гомотетія площині відображає коло, центр якої збігається з центром гомотетии, в концентричне коло. При цьому радіуси кіл зв'язані співвідношенням 
.
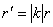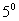Всякі дві нерівні окружності гомотетічни один одному, при цьому, якщо кола не є концентричними, існують дві гомотетии, відображають одну з них в іншу.
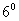
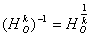
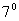
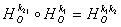
Гомотетія площині є перетворенням подібності першого роду.
Теорема. Всяке перетворення подібності з коефіцієнтом подібності k можна представити як композицію гомотетии і руху.
26. Методи цієї групи мають досить багато спільного. Кожен вивчається, як правило, при розгляді відповідного перетворення, при цьому вирішуються завдання служать для закріплення і більш глибокого засвоєння досліджуваного поняття. Для підвищення ефективності навчання необхідно, щоб, крім початкових уявлень про сам перетворенні, учні вміли виконувати побудову образів фігур при цьому перетворенні, так як використання образу шуканої фігури при побудові є основа кожного з цих методів, їх основна ідея і суть.
Якщо шукану фігуру відразу побудувати важко, то її перетворюють в яку-небудь іншу фігуру, побудова якої можна зробити легше або безпосередньо.
При вивченні цих методів доцільно виділити найбільш характерні ознаки з тим, щоб у майбутньому, аналізуючи задачу, учень міг вибрати відповідний метод.
Діюча програма з геометрії не передбачає використовувати ідею геометричних перетворень як керівної ідеї шкільного курсу геометрії, хоча використання геометричних перетворень при розв'язанні задач на побудову має велике методичне значення [25].
4.2.1 Метод центральної симетрії
Симетрією відносно точки О (центральної симетрією) Z 0 простору називається перетворення простору, яке точку Про відображає на себе, а будь-яку іншу точку М відображає на таку точку М 1, що точка О є серединою відрізка ММ 1.
Даний метод можна застосовувати до тих завдань, в умові яких в тій чи іншій формі вказана точка, яка є центром симетрії шуканої або допоміжної фігури.
Розглянемо задачу: "Через цю точку А провести пряму так, щоб її відрізок з кінцями на даних прямої та кола ділився точкою навпіл".
Рішення. Нехай m і α - дані пряма і коло, CD-шуканий відрізок, З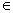 
m, D 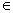а (рис. 3). Тоді Z A (C) = D. Якщо Z A (m) = m 1, то D 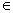m 1 і, отже, D 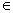а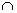 
m 1.Звідси випливає така побудова: будуємо образ m 1 прямий m при симетрії Z A, точки D і Е перетину прямої m 1 з даної окружністю α визначають разом з точкою А шукані прямі DA та ЕА [20].
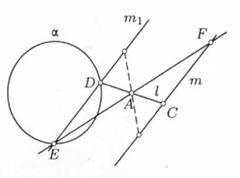
Рис. 3
4.2.2 Метод осьової симетрії
Симетрією простору щодо даної прямої l (осьовою симетрією) S l називається перетворення, яке кожну точку прямої l відображає на себе, а будь-яку іншу точку М простору відображає на таку точку М 1, що пряма l служить серединним перпендикуляром до відрізка ММ 1. Пряма l називається віссю симетрії.
Важко вказати загальні ознаки завдань, що вирішуються методом осьової симетрії. У більш складних завданнях метод осьової симетрії, нерідко спрямляющий ламані лінії в прямі, може бути застосований, якщо в умовах утримується сума або різниця частин деякої ламаної лінії. Можна обмежиться зазначенням, що метод осьової симетрії застосуємо для задач, в умові яких зазначене пряма, яка є віссю симетрії частини елементів фігури. Таку пряму легко встановити за властивостями фігур. Застосування осьової симетрії доцільно для завдань, які легко вирішуються, якщо частина даних розташована по один бік деякої прямої, а решта - по другий.
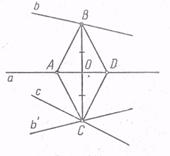
Рис. 4
Розглянемо задачу: "Побудувати ромб так, щоб одна з його діагоналей дорівнювала даному відтинку r і лежала на даній прямій а, а інші дві вершини ромба лежали відповідно на даних прямих b і з".
Аналіз. Нехай (рис.4) ABDC - шуканий ромб, AD = R. Зауважуємо, що задача про побудову ромба зводиться до побудови однієї будь-якої з його вершин, наприклад вершини З. За властивостями ромба точки В і С симетричні відносно прямої а. Тому при осьової симетрії відносно прямої а точка В перетвориться в точку С, а, отже, пряма b - в деяку пряму b ', що проходить через точку С. Таким чином, точка С може бути побудована як точка перетину прямих с і b ', з яких одна дана, а інша легко будується.
Побудова. Будуємо послідовно: пряму b ', симетричну з прямою b відносно прямої а; точку С, загальну для прямих с і b'; прямуПС; точку Про 
НД 
а; точки А і D на прямій а, віддалені від точки О на відстані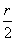 
; ABCD - шуканий ромб.
Доказ зважаючи на його простоти опустимо.
Дослідження. Можливі наступні випадки: 1) з | | b ', рішень немає, 2) з 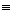b ', рішень нескінченно багато, 3) прямі с і b' перетинаються поза прямою а, одне рішення; 4) прямі с і b 'перетинаються на прямій а, рішень немає [2].
4.2.3 Метод паралельного переносу
Паралельним переносом на вектор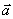 
називається відображення площині на себе, при якому кожна точка М відображається в таку точку М 1, що вектор 
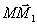дорівнює вектору .
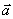Методом паралельного переносу вирішують завдання, при аналізі яких важко знайти залежність між даними елементами, що дозволяє побудувати шукану фігуру (дані елементи віддалені один від одного), але якщо ми якусь частину або всю фігуру перенесемо паралельно в деякому напрямку на певну відстань, то отримаємо допоміжну фігуру, яку легко можна побудувати. Напрямок і величина переносу визначаються так, щоб в допоміжну фігуру увійшло більше число даних.
Розглянемо задачу: "Побудувати опуклий чотирикутник, знаючи три його кута і дві протилежні сторони".
Докладніше: дано два відрізки а і b і три кути α, β, δ. Потрібно побудувати чотирикутник ABCD так, щоб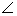 
А = α, 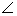В = β, 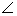D = Δ, AD = A, СВ = b.Передбачається, що 0 ° <α <180 °, 0 ° <β <180 °, 0 ° <δ <180 °.
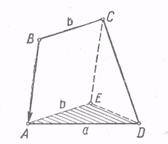
Рис. 5
Аналіз. Припустимо, що ABCD (рис. 5) - шуканий чотирикутник. Перенесемо бік ЗС на вектор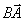 
, І нехай відрізок ВС займе після перенесення положення АЕ. Тоді в 
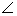AED відомі: AD = a, AE = b, DAE = 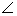BAD - 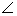BAE = = 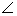A - (180 ° - 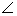B) = α + β - 180 °. За цими даними AED може бути побудований.
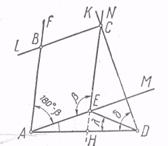
Рис. 6
Побудова . 1) На довільній прямій будуємо відрізок AD = А (рис. 6), 2) Через точку А проводимо промінь AM під кутом α + β - 180 ° до променя AD; 3) Відкладаємо на промені AM відрізок АЕ = b; 4) Будуємо промінь EN, утворює з ЕА кут β і розташований з точкою D по різні сторони від прямої AM;5) Будуємо промінь DK так, щоб 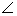ADK дорівнював δ і щоб промінь DK розташовувався по ту ж сторону прямий DE, що і промінь EN; 6) Відзначаємо точку З перетину променів EN і DK - Третю вершину чотирикутника; 7) Четверта вершина У виходить в перетині прямий AF, паралельної РЄ , з прямою CL, паралельної АЕ .
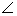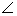Доказ . BAD = ВАЕ + 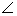DAE = (180 ° - β ) + (α + β - 180 °) = α . 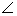ABC = 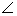СЕА, як кути, сторони яких відповідно паралельні і протилежно направлені. 
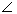СЕА = β з побудови. 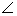ADC = Δ з побудови. Відрізок AD = а з побудови. ЗС = АЕ, як відрізки паралельних між паралельними. Але АЕ = b, а значить, і ВС =b [2].
4.2.4 Метод повороту
Поворотом площини навколо точки О на кут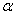 
називається відображення площині на себе, при якому кожна точка М відображається в таку точку М 1, щоОМ = ОМ 1 і кут МОМ 1 = .
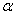Даний метод застосовується до тих завдань, де або частини фігур зближуються в положення, зручне для побудови, або при заданих явно або опосередковано центрі і куті повороту потрібно відшукати дві відповідні точки, що лежать на даних або шуканих фігурах.
Розглянемо задачу: "Земельна ділянка квадратної форми був обгороджений. Від огорожі збереглися два стовпи на паралельних сторонах квадрата. Крім того, залишився стовп в центрі квадрата. Потрібно відновити кордон ділянки ".
Аналіз. Нехай ABCD - шуканий квадрат, О - його центр, М і N - дані точки відповідно на сторонах АВ і CD (рис. 7). Якщо повернути квадрат на 180 ° біля його центру О, то він перетвориться сам у себе. Точка М займе деякий стан М 'на боці CD, а точка N - деяке положення N' на стороні АВ. Після цього неважко вже побудувати прямі АВ і CD і відновити шуканий квадрат.
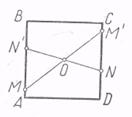
Рис. 7
Побудова. 1) Будуємо точку М ', симетричну М щодо 0, і точку N', симетричну N щодо О. 2) Будуємо прямі MN 'і NM'. 3) Повернемо побудовані прямі близько точки О на 90 °. Чотири побудовані прямі обмежують шуканий квадрат.
Доказ опускаємо.
Дослідження. За змістом завдання неможливий випадок, коли точки М і N розташовуються з точкою О на одній прямій, але не симетричні щодо О. Якщо точки М і N симетричні щодо О, то завдання стає невизначеною. В інших випадках завдання має єдине рішення [2].
4.2.5 Метод подібності
Метод подібності полягає в тому, що спочатку будується деяка фігура, подібна шуканої, але задовольняє не всім поставленим в задачі умов. Потім побудовану допоміжну фігуру замінюємо фігурою, подібною до неї і задовольняє вже всім необхідним умовам [18].
Завдання вирішується методом подібності, якщо її умова можна розділити на дві частини, одна з яких визначає форму фігури з точністю до подібності, а друга - розміри фігури. При вирішенні завдань в класі або розборі завдань з домашнього завдання на цей метод слід задавати учням питання: Що (яка частина) в умові завдання визначає фігуру з точністю до подібності? Що визначає розміри шуканої фігури?
Методичні рекомендації за методом подібності [10]. При розробці методу подоби доцільно класифікувати розв'язувані задачі за способом завдання розмірів шуканої фігури:
1) завдання, в яких розміри шуканої фігури визначаються завданням деякого відрізка;
2) завдання, в яких розміри шуканої фігури визначаються завданням суми або різниці деяких її відрізків;
3) завдання, в яких розміри шуканої фігури визначаються положенням її відносно даних фігур.
Така класифікація зручна, головним чином, тому, що для кожної з трьох груп завдань способи вибору центру подоби різні.
У завданнях з першої групи за центр подоби краще всього вибирати один з кінців відрізка допоміжної фігури, відповідного даному відрізку, через який проходить найбільше число прямолінійних відрізків шуканої фігури, так як при гомотетии лише прямі, що проходять через центр подоби, перетворюються самі в себе. При такому виборі легко знаходити одну точку (другий кінець даного відрізка) шуканої фігури, що в більшості випадків значно полегшує виконання подальшої побудови.
І для завдань другої групи за центр подібності можна вибирати один з кінців побудованої суми або різниці відрізків, відповідної даної. Доцільно розчленувати подібне перетворення: окремо знайти один з відрізків, сума або різниця яких дана, а потім виконати побудову шуканої фігури.
При вирішенні завдань третьої групи центр подоби вже визначається, і в більшості випадків однозначно, розташуванням фігури, подібної шуканої, щодо даних фігур.
У Додатку 4 наведено рішення завдання на метод подібності: "Побудувати трапецію ABCD за кутом А і підставі ПС, якщо відомо, що AB: CD: AD = 1:2:3".
27. Допоміжний елемент – відрізок (або відношення довжин відрізків). Його зручно ввести, якщо фігури подібні. Тоді за допомогою пропорцій або геометричних побудов складається рівняння, в якому цей елемент як член рівняння скорочується, а знайти шуканий стає не важко.
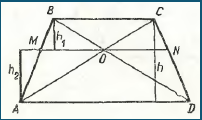
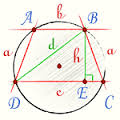
Задача. Основи трапеції – a і b (a < b). Пряма, яка перетинає бічні сторони трапеції в точках М і N, проходить через точку перетину діагоналей паралельно основам. Знайти довжину відрізка МN.
Розв’язання. Введемо як допоміжні елементи h1, h2, h – висоти трикутників відповідно MBO, AMO і BCA (рис.1).
Позначимо х відрізок МО. Трикутники МВО і ABD – подібні: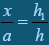 
.
З подібності трикутників АМО і АВС випливає: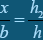 
, отже 
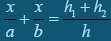. Але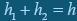 
, тому 
; 
.
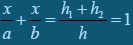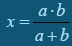Маємо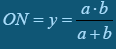 
(обчислюється аналогічно).
28. Застосування кута як допоміжного елемента пов’язано з тригонометрією. Теореми синусів, косинусів, розв’язання трикутників дозволяють звести задачу до доведення тригонометричної тотожності, тригонометричних нерівностей або до розв’язання рівнянь чи нерівностей.
Задача. Довести, що в трикутнику АВС: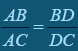 
, де D – точка перетину бісектриси кута ВАС зі стороною ВС.
Доведення. Введемо позначення (рис.1),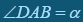 
, 
. 
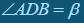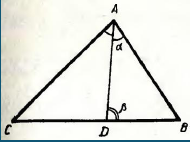
За теоремою синусів з трикутника АDВ дістаємо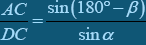 
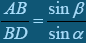. З трикутника CAD випливає , або 
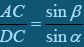. Отже, 
.
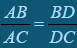29. Введення площі як допоміжного елемента аналогічне введенню лінійного елемента – відрізка. Порівнюючи площі фігур, можна дістати рівняння відносно невідомих задачі або необхідне співвідношення у вигляді формули.
Краще знаходити чи порівнювати ті площі, сума (різниця) яких дає площу заданої фігури або відношення площ тих фігур, у яких лінійні елементи – шукані, або є компонентами співвідношення у вигляді формули.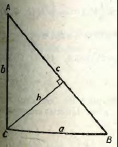 
Задача. У прямокутному трикутнику АВС (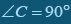 
) 
(h – висота). Довести.
Доведення. Позначимо S площу трикутника АВС (рис. 1).
Тод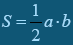і 
і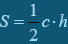 
, отже, 
.
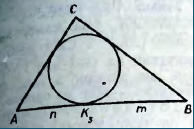
30. При застосуванні периметра як допоміжного елемента використовують наступні твердження:
1) якщо в трикутник АВС вписано коло, де К1, К2, К3 – точки дотику кола до сторін ВС, АС, АВ (рис.1), то :
АК3 = АК2 = р – а;
ВК3 = ВК2 = р – b;
СК3 = СК2 = р – с.
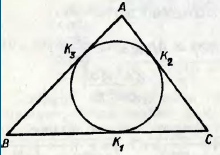
Рис.1
2) відстані від точок дотику зовні вписаного кола, які належать продовженню двох сторін трикутника АВС до їх спільної вершини, дорівнюють півпериметру трикутника АВС (рис. 2).
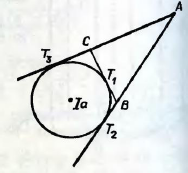
Рис. 2
Задача. У прямокутному трикутнику АВС ( 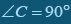) АК3 = т, ВК3 = п. Знайти площу трикутника АВС.
Розв’язання. Введемо периметр 2р. Тоді АК3 = р – а, ВК3 = р – b (рис. 3),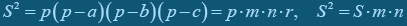 
, звідки 
.
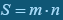31. Метод допоміжних точок
При допоміжних побудовах можна користуватися точками, про які в умові задачі нічого не повідомляється. Ці точки називають допоміжними. Вивчення таких точок і їх властивостей збагачує досвід розв’язання задач, допомагає правильно та раціонально намітити схему розв’язку, а головне – зробити усвідомленими допоміжні побудови.
Використовують такі допоміжні точки при розв’язуванні задач:
· допоміжні точки – чудові точки трикутника: ортоцентр, центроїд, інцентр, центр зовні вписаного кола;
· допоміжна точка – центр кола;
· симетричні точки.
32. Метод допоміжних прямих
Використовують такі побудови допоміжних прямі при розв’язуванні задач:
· побудова паралельних прямих;
· побудова перпендикулярних прямих;
· побудова рівних відрізків та відрізків певної довжини.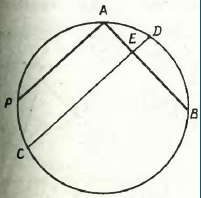 
Рис. 1
Задача. Довести, що кут з вершиною в середині кола дорівнює півсумі дуг, що знаходяться між його сторонами.
Доведення. Нехай хорди АВ і DC перетинаються в точці Е (рис.1). Доведемо, що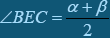 
, де α і β – градусні виміри дуг ВС і AD. Проведемо хорду АР, паралельну хорді DC. Оскільки дуга РС дорівнює дузі АD, то 
і 
33. Метод допоміжних фігур
Найчастіше використовують такі допоміжні фігури при розв’язуванні задач:
· допоміжна фігура – трикутник;
· допоміжна фігура – паралелограм;
· допоміжна фігура – трапеція.
Задача.Побудуйте трикутник за даною стороною a, прилеглим до неї кутом α і сумою двох інших сторін b.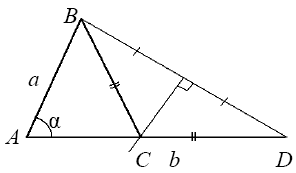 
Розв’язання.
Аналіз. Припустимо, що шуканий трикутник уже побудовано. За даними відрізками і кутом між ними можна побудувати ∆ABD. Вершиною С шуканого трикутника буде така точка, для якої ВС=CD. Виходячи з рівнобедреного трикутника CBD, у якого медіана є висотою, точка С має лежати на серединному перпендикулярі сторони BD.
Побудова.
1) За двома сторонами і кутом між ними будуємо ∆ABD.
2) Будуємо серединний перпендикуляр сторони BD.
3) Цей серединний перпендикуляр в перетині із стороною AD дасть точку С.
4) Побудувавши сторону ВС, отримаємо шуканий трикутник.
Доведення. ∆АВС є шуканим, так як AB=a, 
A=α, AC+BC=b.
Дослідження. Задача має розв’язок, якщо a b.