Властивості квадрата
Усі кути квадрата — прямі.
Діагоналі квадрата перетинаються і точкою перетину діляться навпіл.
Діагоналі квадрата рівні.
Діагоналі квадрата перетинаються під прямим кутом.
Діагоналі квадрата є бісектрисами його кутів.
Ознаки квадрата
Якщо в прямокутнику діагоналі перетинаються під прямим кутом, то цей прямокутник є квадратом.
Якщо у ромба діагоналі рівні, то цей ромб є квадратом.
Якщо в чотирикутнику всі сторони рівні і всі кути рівні, то цей чотирикутник є квадратом.
11. Трапеція та її властивості
Трапецією називається чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.
Паралельні сторони трапеції називають основами, а непаралельні сторони – бічними.
Наприклад: ABCD – трапеція, оскільки 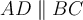 , АВ∦CD, сторони BC і AD – основи трапеції, АВ і СD – бічні сторони трапеції.
, АВ∦CD, сторони BC і AD – основи трапеції, АВ і СD – бічні сторони трапеції.
Висотою трапеції називають перпендикуляр, проведений із будь-якої точки однієї з основ на пряму, що містить другу основу (або відстань між основами трапеції).
Наприклад: MN – висота трапеції ABCD.
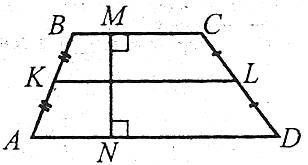
Середньою лінією трапеції називають відрізок, що сполучає середини бічних сторін трапеції.
Наприклад: KL – середня лінія.
Властивості трапеції
1. Сума кутів трапеції, прилеглих до бічної сторони, дорівнює 180°.
Наприклад: 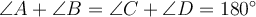 .
.
2. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.
Наприклад: 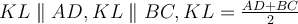 .
.
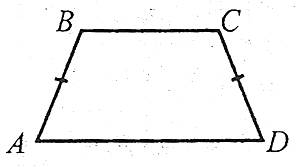
Трапецію, у якої бічні сторони рівні, називають рівнобічною (рівнобедреною) трапецією.
Наприклад: ABCD – рівнобічна трапеція.
Властивості рівнобічної трапеції
У рівнобічній трапеції:
1. Кути при основі рівні:  .
.
2. Діагоналі рівні: AC=BD.
Прямокутною називають трапецію, у якої одна з бічних сторін перпендикулярна до основ. Ця бічна сторона є висотою трапеції.
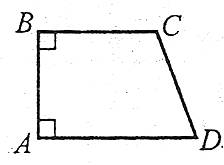
Якщо у рівнобічній трапеції діагоналі взаємно перпендикулярні, то її висота дорівнює середній лінії:
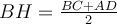 .
.
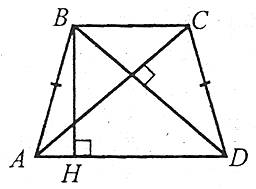
Коло можна описати лише навколо рівнобічної трапеції.
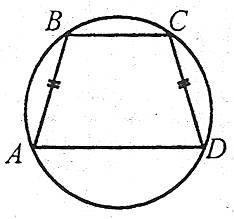
Висота рівнобічної трапеції, у яку можна вписати коло, є середнім геометричним між її основами:
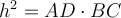 .
.
Якщо у рівнобічну трапецію вписано коло, то її бічна сторона дорівнює середній лінії:
 .
.
12. Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. Если же соединить отрезком середины оснований, получится вторая средняя линия трапеции. Итак, вторая средняя линия трапеции – это отрезок, соединяющий середины оснований трапеции.
Властивості:
1. Средние линии трапеции в точке пересечения делятся пополам.
2. Вторая средняя линия трапеции проходит через точку пересечения диагоналей
3. Прямая, содержащая вторую среднюю линию трапеции, проходит через точку пересечения прямых, содержащих боковые стороны
4. В равнобочной трапеции средние линии перпендикулярны
5. В равнобочной трапеции вторая средняя линия перпендикулярна основаниям
6. Если средние линии трапеции равны, ее диагонали перпендикулярны
13. Середня лінія фігур - відрізок, що з'єднує середини двох сторін даної фігури.
якщо в опуклому чотирикутнику середня лінія утворює рівні кути з діагоналями чотирикутника, то діагоналі рівні.
• довжина середньої лінії чотирикутника менше півсумі двох інших сторін або дорівнює їй, якщо ці сторони паралельні, і тільки в цьому випадку.
• середини сторін довільного чотирикутника - вершини паралелограма. Його площа дорівнює половині площі чотирикутника, а його центр лежить на точці перетину середніх ліній. Цей паралелограм називається паралелограмом Варіньона;
• Точка перетину середніх ліній чотирикутника є їхньою спільною серединою і ділить навпіл відрізок, що з'єднує середини діагоналей. Крім того, вона є центроїдом вершин чотирикутника.
3. Властивості трапеції:
• середня лінія паралельна основам трапеції і дорівнює їх півсумі;
• середини сторін рівнобедреної трапеції є вершинами ромба.
14.Коло, круг. Довжина кола, дуги кола
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки —центра кола.
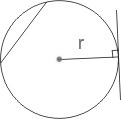
Рис. 1. Коло
Радіус кола — відстань від точок кола до його центра. Радіус кола зазвичай позначається буквами r,R.
Хорда — відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Діаметр зазвичай позначають буквами d,D.
Дотична — пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. Через будь-яку точку, що лежить поза колом і належить площині кола, можна провести дві різні дотичні.
Пряма, що має з колом дві спільні точки, називається січною.
Довжиною кола називається границя послідовності периметрів правильних багатокутників, які вписані в дане коло, при необмеженому збільшенні кількості сторін. Довжина кола C обчислюється за формулою
C=πd
або
C=2πr
Довжина дуги кола з кутовою величиною в α∘ обчислюється за формулою
l=πrα180
Круг
Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка — центр круга. Радіус — задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.
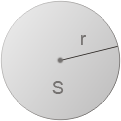
Рис. 2. Круг
Площою круга називається границя послідовності площ правильних багатокутників, вписаних в дане коло, при необмеженому збільшенні кількості сторін. Площа круга обчислюється за формулою:
S=πr2
Сектором називається частина круга, що обмежена двома його радіусами.
Площа сектора з кутовою величиною дуги α∘ обчислюється за формулою
Sc=πr2α360
15. Площа круга дорівнює половині добутку довжини кола, що її обмежує, на радіус:
S = (lR) / 2 = πR2 = (πd2) / 4
Круговий сектор — частина круга, що лежить усередині відповідного центрального кута.
Площа кругового сектора визначається за формулою: S = (πR2n) / 3600.
Круговий сегмент — спільна частина круга й півплощини.
16. Кожна з частин площини, на які будь-який кут розбиває площину, називається плоским кутом. Плоскі кути, які мають спільні сторони, називаються доповняльними кутами, а їхня сума дорівнює 360. Кут, уписаний у коло — кут, вершина якого лежить на колі, а сторони перетинають дане коло.
Уписаний у коло кут, сторони якого перетинають коло у двох певних точках, дорівнює половині кута між радіусами кола, проведеними в ці точки, або доповнює половину цього кута до 180°.
Якщо уписаний кут є гострим, то він дорівнює половині кута між радіусами, а якщо уписаний кут є тупим, то він доповнює його до 180°. Усі уписані кути, сторони яких проходять через дві певні точки кола, а вершини лежать з одного боку від прямої, що з’єднує ці точки, рівні.
Кути, сторони яких проходять через кінці діаметра, є прямими.
Центральний кут — це плоский кут, вершина якого є центром кола, а сторони кута перетинають коло.
Дуга кола, що відповідає центральному куту, — це частина кола, яка знаходиться всередині кута.
Градусна міра дуги — градусна міра відповідного центрального кута.
Кут, уписаний у коло, дорівнює половині відповідного центрального кута.
17. Коло називається описаним навколо трикутника, якщо всі вершини трикутника лежать на колі. Кажуть, що трикутник є вписаним у коло.
Навколо будь-якого трикутника можна описати коло і лише одне. Центр кола, описаного навколо трикутника, є точкою перетину перпендикулярів, проведених через середини сторін трикутника, тобто точка перетину серединних перпендикулярів до сторін трикутника.
Зверніть увагу! Щоб знайти центр описаного кола, достатньо провести серединні перпендикуляри до двох сторін трикутника.
Щоб описати навколо трикутника коло, треба знайти центр кола і радіусом, що дорівнює відстані від центра кола до будь-якої вершини трикутника, побудувати коло.
Через будь-які три точки, що не лежать на одній прямій, можна провести коло і лише одне.
Центром кола, описаного навколо прямокутного трикутника, є середина його гіпотенузи, а радіус дорівнює її половині.
Якщо одна із сторін уписаного в коло трикутника дорівнює його діаметру, то цей трикутник прямокутний.
18. Вписані й описані чотирикутники
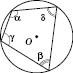
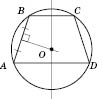
Теорема 1. Навколо чотирикутника можна описати коло тоді й тільки тоді, коли сума його протилежних кутів дорівнює 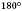 .
.
На рисунку  .
.
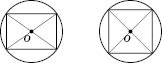
Із цього випливає, що коло можна описати навколо прямокутника (рисунок нижче зліва), зокрема квадрата (рисунок справа), його центром буде точка перетину його діагоналей. Радіус — половина діагоналі.
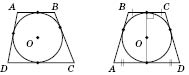
Коло можна описати навколо трапеції тоді й тільки тоді, коли вона є рівнобічною (див. рисунок). Центром кола є точка перетину середніх перпендикулярів до сторін. Навколо паралелограма та трапеції загального виду описати коло не можна. (Зокрема, навколо ромба не можна описати коло.)
еорема 2. Чотирикутник тоді й тільки тоді можна описати навколо кола, якщо суми його протилежних сторін дорівнюють одна одній.
На рисунку 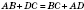 .
.
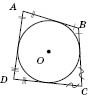
Отже, коло можна вписати в ромб (зокрема у квадрат), але не можна в прямокутник або паралелограм загального виду.
Центр кола, вписаного в ромб, є точкою перетину діагоналей (рисунок нижче зліва). Радіус кола дорівнює половині висоти ромба, а у квадраті — половині сторони (рисунок справа).
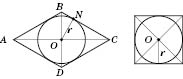
Зверніть увагу: радіус вписаного в ромб кола (ON) — це висота прямокутного трикутника BOC, яка проведена з вершини прямого кута і має всі властивості висоти прямокутного трикутника, що проведена з вершини прямого кута.
Теорема 3. Трапецію тоді й тільки тоді можна описати навколо кола, коли сума її основ дорівнює сумі бічних сторін (рисунок нижче зліва). Центр цього кола — точка перетину бісектрис кутів трапеції. Радіус дорівнює половині висоти трапеції. У випадку рівнобічної трапеції центр вписаного кола лежить на середині висоти трапеції, яка проходить через середини основ (рисунок справа). Бічна сторона трапеції у цьому випадку дорівнює її середній лінії.
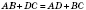
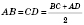
19. Опуклий многокутник називається правильним, якщо в нього всі сторони рівні й усі кути рівні.
Многокутник називається вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до деякого кола.
Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним навколо кола.
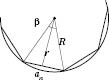
Вписане й описане кола правильного многокутника мають один і той самий центр, який називається центром многокутника. Кут, під яким видно сторону правильного многокутника із цього центра, називається центральним кутом многокутника. На рисунку  — центральний кут многокутника.
— центральний кут многокутника.
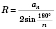 ;
;
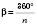 ;
;
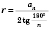 .
.
Теорема 2. Правильні опуклі n-кутники подібні. Зокрема, якщо у них сторони рівні, то такі n-кутники рівні.
Правильний трикутник (рівносторонній)
На рисунку:
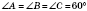 ;
;
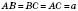 ;
;
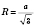 ;
; 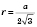 ;
;
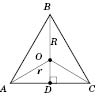
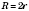 ;
;
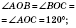
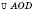 :
: 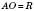 ;
;
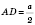 ;
; 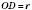 ;
; 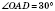 ;
;
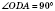 ;
; 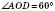 ;
;
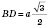 ;
; 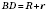 ;
; 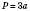 ;
;
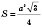 .м
.м
Правильний чотирикутник (квадрат)
На рисунку: 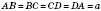 ;
;
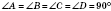 ;
;
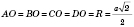 ;
; 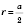 ;
;
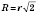 ;
; 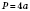 ;
; 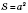 ;
;
 — рівнобедрені прямокутні трикутники.
— рівнобедрені прямокутні трикутники.
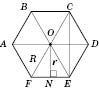
Правильний шестикутник
На рисунку: 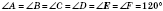 ;
;
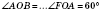 ; сторона а;
; сторона а;
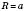 ;
; 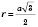 ;
;
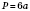 ;
; 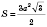 ;
;
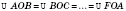 — рівноcторонні трикутники;
— рівноcторонні трикутники;
ABCD — рівнобічна трапеція з кутами 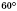 і
і 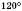 ;
;
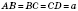 ,
, 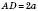 ;
;
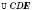 — рівнобедрений;
— рівнобедрений;
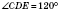 ;
; 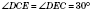 ;
;
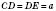 ;
; 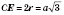 .
.
Діагональ 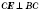 .
.
Зверніть увагу: якщо з’єднати послідовно середини сторін правильного n-кутника, отримаємо правильний n-кутник (див. рисунки).
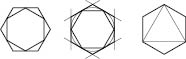
Якщо через вершини правильного n-кутника провести дотичні до описаного навколо нього кола, отримаємо правильний n-кутник.
Якщо з’єднати через одну вершини правильного 2n-кутника, отримаємо правильний n-кутник.
Довжина кола
Теорема. Відношення довжини кола до його діаметра не залежить від кола, тобто є одним і тим самим числом для будь-яких двох кіл.
Це число позначається  .
.
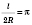 , де l — довжина кола, R — радіус.
, де l — довжина кола, R — радіус.
Отже, 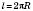 або
або 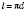 ;
;
 — число ірраціональне,
— число ірраціональне, 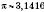 .
.
Довжина дуги кола, яка відповідає центральному куту 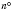 :
: 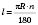 .
.
20.
21.
22.Декартові координати на площині: основні поняття, означення, співвідношення. Координатний метод розв'язування геометричних задач.
Нагадаємо, що для введення системи координат на площині через деяку точку О необхідно провести дві взаємно перпендикулярні прямі Ох і Оу, вибрати на кожній із них напрям (його позначають стрілкою) і одиничний відрізок (рис.).
Т 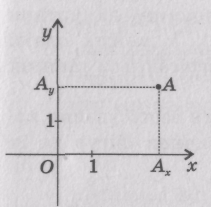 очку О називають початком координат, площину, на якій проведені прямі, —координатною площиною, а самі прямі Ох і Оу — координатними осями (абоосями координат). Початок координат ділить кожну з осей на дві півосі: додатну (на ній позначається стрілка) і від'ємну.
очку О називають початком координат, площину, на якій проведені прямі, —координатною площиною, а самі прямі Ох і Оу — координатними осями (абоосями координат). Початок координат ділить кожну з осей на дві півосі: додатну (на ній позначається стрілка) і від'ємну.
Тепер будь-якій точці А даної площини можна однозначно поставити у відповідність впорядковану пару чисел — координати цієї точки. Для цього з точки А проведемо перпендикуляри ААх  Ох і ААу
Ох і ААу  Оу.
Оу.
П 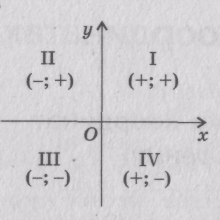 ерша координата точки А — абсциса (позначається буквою х) — є додатним числом, якщо точка Ахлежить на правій півосі осі Ох, або від'ємним числом, якщо точка Ах лежить на лівій півосі осі Ох. При цьому модуль числа х дорівнює довжині відрізкаОА х . Аналогічно визначається друга координата точки А — ордината (позначається буквою у): це додатне число, якщо точка А лежить на верхній півосі осі Оу, або від'ємне число, якщо точка Алежить на нижній півосі осі Оу, а модуль числа удорівнює довжині відрізка ОА . Координати точки Азаписують так: А(х; у). При цьому абсцису точки вказують першою, а ординату — другою.
ерша координата точки А — абсциса (позначається буквою х) — є додатним числом, якщо точка Ахлежить на правій півосі осі Ох, або від'ємним числом, якщо точка Ах лежить на лівій півосі осі Ох. При цьому модуль числа х дорівнює довжині відрізкаОА х . Аналогічно визначається друга координата точки А — ордината (позначається буквою у): це додатне число, якщо точка А лежить на верхній півосі осі Оу, або від'ємне число, якщо точка Алежить на нижній півосі осі Оу, а модуль числа удорівнює довжині відрізка ОА . Координати точки Азаписують так: А(х; у). При цьому абсцису точки вказують першою, а ординату — другою.
Зауважимо, що ординати точок осі Ох дорівнюють нулю, абсциси точок осі Оу також дорівнюють нулю, а початок координат має координати О (0; 0).
Вісь Ох (зазвичай вона горизонтальна) називають віссю абсцис, вісь Оу — віссю ординат, а введену таким способом систему координат — прямокутною декартовою на честь Рене Декарта, який першим застосував її у своїх дослідженнях.
Осі координат ділять площину на чотири частини (координатні чверті). У межах однієї чверті знаки координат точок зберігаються такими, які вказані на рисунку.
Отже, місце точки на площині визначається парою чисел - координатами точки. Ми вирушаємо на вулицю Відрізок.
На вулиці Відрізок живуть цікаві задачі. Вони оселилися тут після того, як було встановлено формулу відстані між двома точками.
Ви знаєте, як знаходити відстань між двома точками, заданими своїми координатами на координатній прямій: для точок А (х1) і В (х2):
АВ = | х2 - х 1 |.
Навчимося знаходити відстань між точками
А (х1; у1) і В (х2; у2), заданими на площині ху.
Розглянемо випадок, коли відрізок АВ не перпендикулярний до жодної з координатних осей (рис.).
Через точки А і В проведемо прямі, перпендикулярні до координатних осей. Отримаємо прямокутний трикутникАСВ.
Очевидно, що ВС = |х2 - х1|, АС = |у2 - у1|. Звідси за теоремою Піфагора
АВ 2 = ВС 2 + АС 2 = |х2 - х1| 2 + |у2 - у1| 2.
Тоді формулу відстані між точками А (х1; у1) і В (х2; у2) можна записати так:
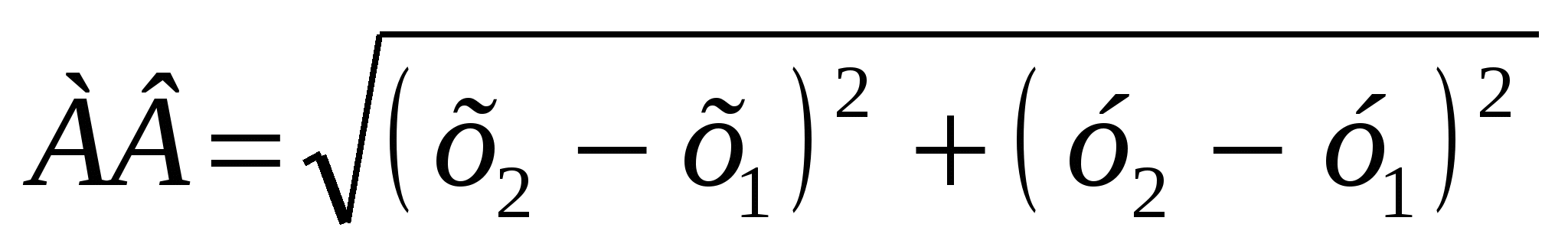 (формула відстані між двома точками).
(формула відстані між двома точками).
Отже, Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат.
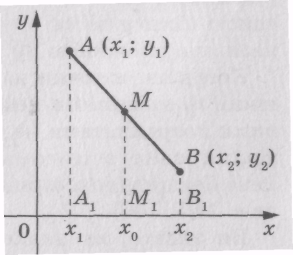
Нехай А(х1; у1) і В(х2; у2) — точки площини ху. Навчимося знаходити координати (х0; у0) точки М — середини відрізка АВ.
Знов-таки розглянемо випадок, коли відрізок АВ не перпендикулярний до жодної з координатних осей (рис.). Вважатимемо, що х2 > х1 (випадок, коли х2 < х1, розглядається аналогічно). Через точки А, М і В проведемо прямі, перпендикулярні до осі абсцис, які перетнуть цю вісь відповідно в точках А1, М1 і В1. За теоремою Фалеса А1М1 = М1В1, тобто | х0 - х1| = | х2 - х0|.
 Оскільки х2 > х0 > х1, то можемо записати:
Оскільки х2 > х0 > х1, то можемо записати:
х0 - х1 = х2 - х0. Звідси
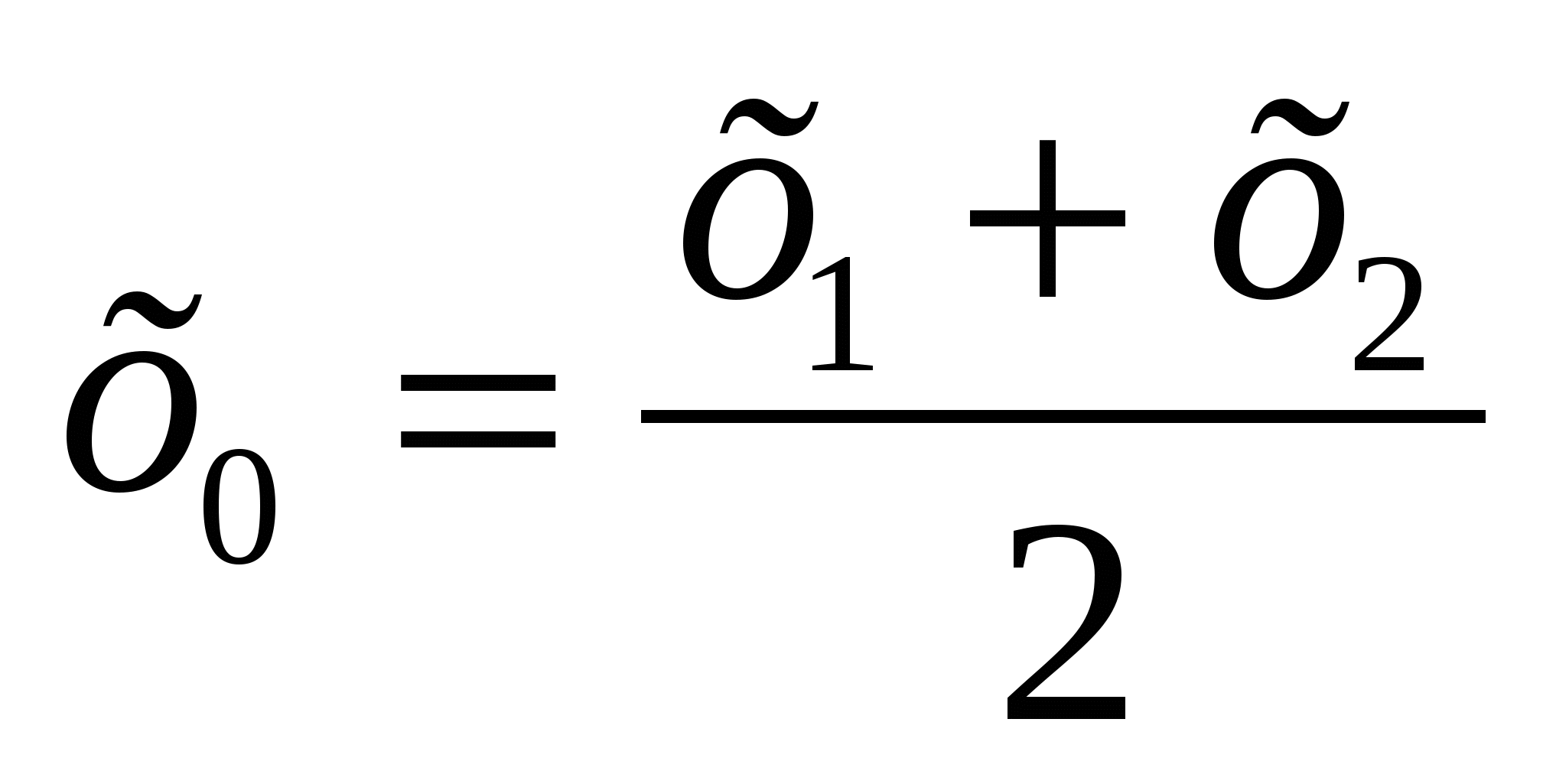
Аналогічно можна показати, що
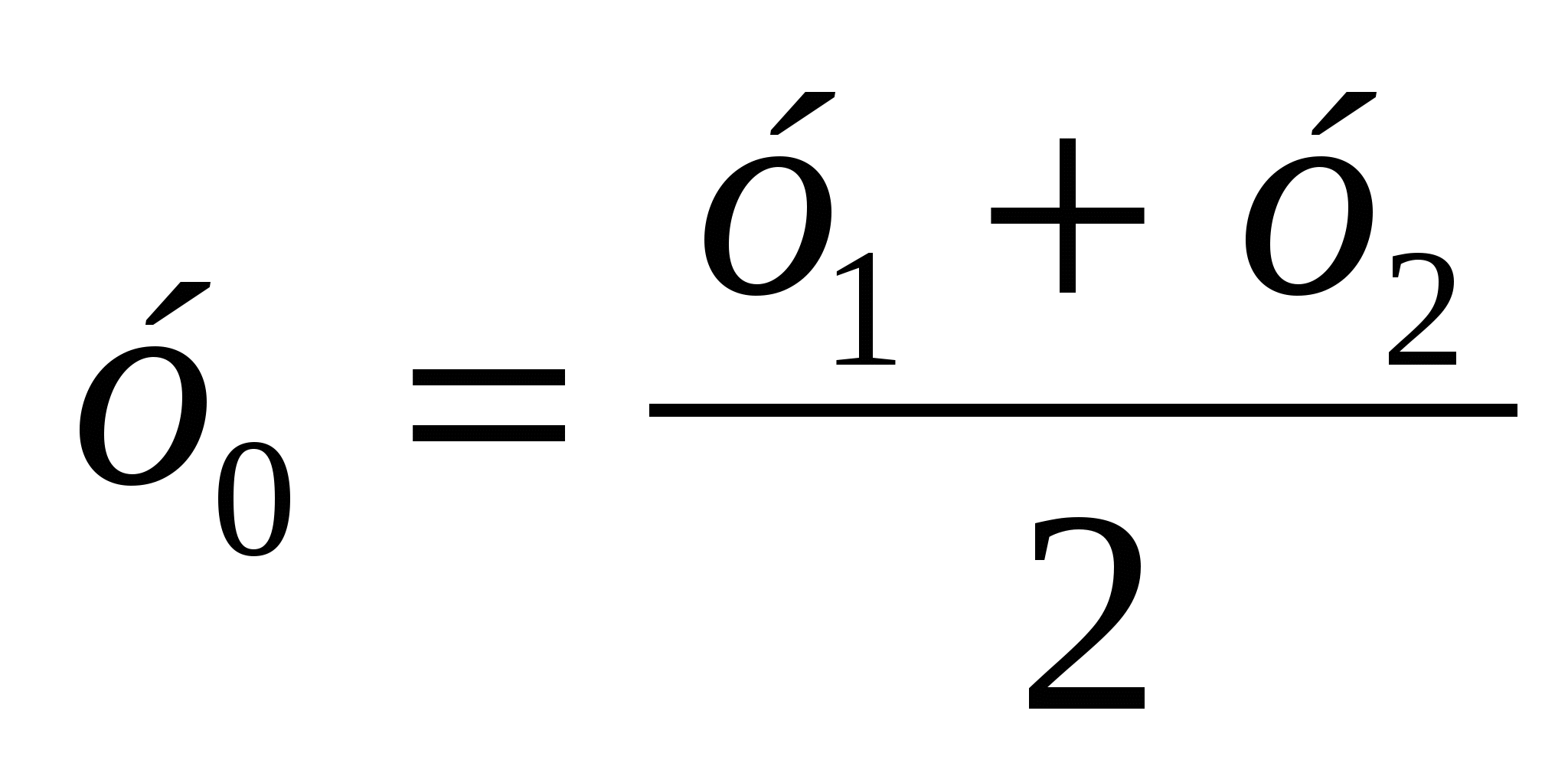
Отже, кожна координата середини відрізка дорівнює півсумі відповідних координат його кінців.
24. Вектори на площині: основні поняття, означення, дії, співвідношення. Векторний метод розв'язування геометричних задач.
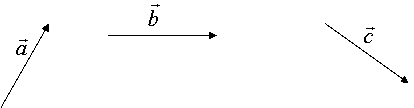
Вектор - це напрямлений відрізок або вектор - це паралельний перенос.
Вектори позначають: 
|
Або за початком і кінцем
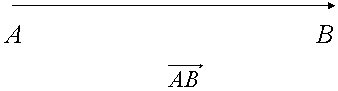
|
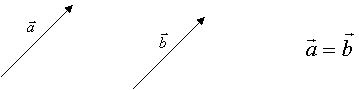
Якщо початок і кінець співпадають, вектор називають нульовим або О Два вектори називають рівними, якщо їх довжини рівні, а напрями співпадають
Вектори, які лежать на паралельних прямих, називають колінеарними.
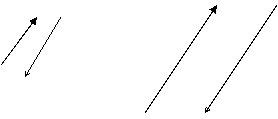
|
(а якщо ця умова не виконується, то не колінеарними)
Вектори, які лежать в одній площині, називають компланарними (а якщо
ця умова не виконується, не компланарними).
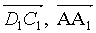 - не компланарні
- не компланарні
 - компланарні
- компланарні
2. Додавання векторів Правило трикутника
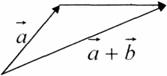
Правило паралелограма
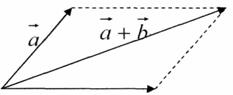 Сумою двох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить з цієї ж точки.
Сумою двох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить з цієї ж точки.
Правило паралелепіпеда
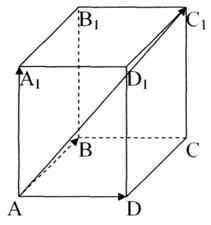
Сумою трьох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелепіпеда, побудованого на цих векторах, яка виходить з цієї ж точки.
Властивості додавання
1) 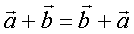 — комутативність
— комутативність
2) 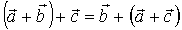 — асоціативність
— асоціативність
3) 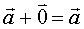
4) якщо 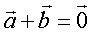 , то
, то 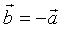 і називається протилежним
і називається протилежним
Віднімання векторів
Щоб відняти два вектори, потрібно відкласти їх від спільної точки, з'єднати кінці і стрілку поставити до того вектора, від якого віднімаємо
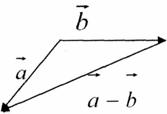
Множення вектора на число.
Добутком  на число k називають вектор, який має довжину
на число k називають вектор, який має довжину  і співнапрямлений з
і співнапрямлений з 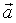 , якщо k > 0 та протилежний до нього, якщо k < 0.
, якщо k > 0 та протилежний до нього, якщо k < 0.
|
Як видною, при множенні вектора на число, одержуємо колінеарні вектори. Справедливе обернене твердження, яке?.
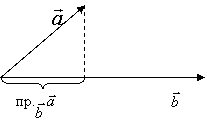
Скалярний добуток векторів.
Скалярним добутком двох векторів називають число, що дорівнює добутку довжин цих векторів на косинус кута між ними.
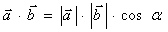 , де
, де 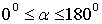
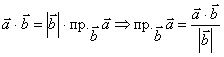
Якщо 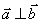 то
то 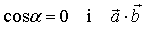 і навпаки , якщо
і навпаки , якщо 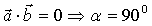 , тобто
, тобто 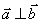 .
.
24. Рухи на площині, види рухів, їх властивості. Рівність фігур
Рухом - перетворення однієї фігур у іншу коли вона зберігає відстань між точками, тобто. переводить будь-які дві точки X і Y однієї фігур у точки X , Y інший постаті отжеXY = X Y
Властивості руху: 1. Крапки, що лежать на прямий, під час руху переходить до точки, що лежать на прямий, й тепло зберігається порядок їх взаємного розташування.Це означає, що й A, B, З, що лежать на прямий, переходить до точки A1,B1,З1. Те ці точки також лежать на прямий; якщо точка B лежить між точками A і З, то точка B1 лежить між точками A1 і З1.
Доказ. Нехай точка B прямийAC лежить між точками A і З.Докажем, що точки A1,B1,З1 лежать в одній прямий.
Якщо точка A1,B1,З1 не лежать на прямий, всі вони є вершинами трикутника. Тому A1З1 < A1B1 + B1З1. За визначенням руху це означає, щоAC<AB+BC. Проте з властивості виміру відрізківAC=AB+BC.
Ми дійшли протиріччю. Отже, точка B1 лежить на жіночих прямий A1З1. Перше твердження теореми доведено.
Покажемо тепер, що вищу точку B1 лежить між A1 і З1. Припустимо, що вищу точку A1 лежить між точками B1 і З1. Тоді A1B1 + A1З1 = B1З1, і, отже,AB+AC=BC. Але суперечить нерівностіAB+BC=AC. Отже, точка A1 неспроможна лежати між точками B1 і З1.
Аналогічно доводимо, що вищу точку З1 неспроможна лежати між точками A1 і B1.
Оскільки із трьох точок A1,B1,З1 одна лежить між двома іншими, то цієї точкою може лише B1. Теорему доведено повністю.
2. При русі прямі переходить до прямі,полупрямие – вполупрямие, відтинки – в відтинки
3. При русі зберігаються кути міжполупрямими.
Доказ. НехайAB іAC – двіполупрямие, які виходять із точки A, не що лежать на неї прямий. При русі ціполупрямие переходить до деякіполупрямие A1B1 і A1З1. Оскільки рух зберігає відстань, то трикутники ABC і A1B1З1 рівні щодо третього ознакою рівності трикутників. З рівності трикутників слід рівність кутівBAC і B1A1З1, що потрібно було довести.
4. Рух переводить площину на площину.
Докажем це властивість. Нехай a - довільна площину. Зазначимо у ньому будь-які трикрапку A, B, З, не що лежать в одній прямий. Проведемо них площину a'.
Докажем, що з аналізованому русі площину a перетворюється на площину a'.
Нехай X - довільна точка площині a. проведемо неї якусь пряму a у площині a, що перетинає трикутникABXC у двох точках Y і Z. Пряма а перейде під час руху в деяку пряму a'. Крапки Y і Z прямий a перейдуть у точки Y' і Z', належать трикутникуA'B'C', отже, площині a'.
Отже пряма a' у площині a'. Крапка X на своєму шляху перетворюється на точку X' прямий a', отже, і в пласкості a', що потрібно було довести.
У просторі, як і і площині, дві постаті називаються рівними, якщо вони поєднуються рухом.
III. Види руху: симетрія щодо точки, симетрія щодо прямий, симетрія щодо площині, поворот, рух, паралельний перенесення.
>Симметрия щодо точки
Нехай Про - фіксована точка і X - довільна точка площині.Отложим на продовженні відрізкаOX за точкуO відрізокOX', рівнийOX. Крапка X' називається симетричній точці X щодо точкиO. Крапка, симетрична точціO, є сама точкаO. Вочевидь, що вищу точку, симетрична точці X', є точка X.
Перетворення постаті F на постать F', у якому кожна її точка X перетворюється на точку X',симметричную щодо даної точціO, називається перетворенням симетрії щодо точкиO. У цьому постаті F і F' називаються симетричними щодо точкиO.
Якщо перетворення симетрії щодо точкиO переводить постать F у собі, вона називається>центрально-симметричной, а точкаO називається центром симетрії.
Наприклад, паралелограм єцентрально-симметричной постаттю. Його центром симетрії є точка перетину діагоналей.
Теорему: Перетворення симетрії щодо точки є рухом.
Доказ. Нехай X і Y - дві довільні точки постаті F. Перетворення симетрії щодо точкиO переводить в точки X' і Y'. Розглянемо трикутникиXOY іX'OY'. Ці трикутники рівні за першим ознакою рівності трикутника. Але вони кути при вершиніO рівні як вертикальні, аOX=OX',OY=OY' з визначення симетрії щодо точкиO. З рівності трикутників слід рівність сторін:XY=X'Y'. Отже, що симетрія щодо точкиO є рух. Теорему доведено.
>Симметрия щодо прямий
Нехай g - фіксована пряма. Візьмемо довільну точку X і опустимо перпендикулярAX зв пряму g. На продовженні перпендикуляра за точку A відкладемо відрізокAX', рівний відтинкуAX. Крапка X' називається симетричній точці X щодо прямий g. Якщо точка X лежить на жіночих прямий g, то симетрична їй точка є сама точка X. Вочевидь, що вищу точку, симетрична точці X', є точка X.
Перетворення постаті F на постать F', у якому кожна її точка X перетворюється на точку X',симметричную щодо даної прямий g, називається перетворенням симетрії щодо прямий g. У цьому постаті F і F' називаються симетричними щодо прямий g.
Якщо перетворення симетрії щодо прямий g переводить постать F у собі, ця постать називається симетричній щодо прямий g, а пряма g називається віссю симетрії постаті.
Наприклад, прямі, які відбуваються через точку перетину діагоналей прямокутника паралельно його сторонам, є осями симетрії прямокутника. Прямі у яких лежать діагоналі ромбу, є його осями симетрії.
Теорему: Перетворення симетрії щодо прямий є рухом.
Доказ. Приймемо цю пряму за вісь удекартовой системи координат. Нехай довільна точка A (>x;y) постаті F перетворюється на точку A' (>x';y') постаті F'. З визначення симетрії щодо прямий слід, що з точок A і A' рівні ординати, аабсцисси відрізняються тільки знайома: x' = -x.
Візьмемо дві довільні точки A (>x;y) і B (>x;y). Вони перейдуть у точки A' (->x;y) і B' (->x;y).
Маємо:
AB2=(x2-x1)2+(y2-y1)2
A'B'2=(-x2+ x1) 2+(y2-y1)2
Звідси видно, щоAB=A'B'. Отже, що перетворення симетрії щодо прямий є рух. Теорему доведено.








