Элементы треугольника
Взаємне розміщення прямих на площині
Дві прямі на площині можуть:
• збігатися;
• бути паралельними (тобто не перетинатися);
• мати одну спільну точку.
(Дійсно, якщо б дві прямі могли мати хоча б дві спільні точки, то через ці дві точки проходили б дві різні прямі, що суперечить аксіомі І, п. 2).
2. Треугольник — это геометрическая фигура, состоящая из трех точек, попарно соединенных между собой отрезками.
Теорема: Сумма углов треугольника равна 1800.
Следствие: У любого треугольника хотя бы два угла острые.
Виды треугольника
По сторонам:
1. Равнобедренный
2. Равносторонний
3. Произвольны
По углам
1. Остроугольный
2. Тупоугольный
3. Прямоугольный
Элементы треугольника
Медиана треугольника – это отрезок, исходящий из вершины треугольника к противолежащей стороне и делящий его пополам.
Высота треугольника – это отрезок, исходящий из вершины треугольника к противолежащей стороне под прямым углом.
Биссектриса треугольника – это отрезок, исходящий из вершины треугольника и делящий этот угол пополам.
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
Теорема: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Следствие: Внешний угол треугольника больше любого угла треугольника, не смежного с ним.
Соотношения между сторонами и углами треугольника
В любом треугольнике против большего угла лежит большая сторона, против меньшего угла лежит меньшая сторона.
В любом треугольнике против большей стороны лежит больший угол, против меньшей стороны – меньший угол.
Неравенство треугольника
Длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.
Замечательные точки треугольника
1. Высоты треугольника пересекаются в одной точке.
2. Медианы треугольника пересекаются в одной точке.
3. Биссектрисы треугольника пересекаются в одной точке.
4. Серединные перпендикуляры треугольника пересекаются в одной точке.
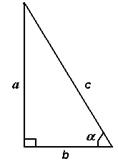
3. Соотношения между сторонами и углами треугольника.
| 
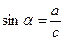
| В прямоугольном треугольнике синус угла равен отношению противолежащего катета к гипотенузе. |
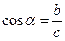
| В прямоугольном треугольнике косинус угла равен отношению прилежащего катета к гипотенузе. | |
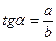
| В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. | |
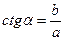
| В прямоугольном треугольнике котангенс угла равен отношению прилежащего катета к противолежащему. |
Теорема 24. (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема 25. (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
С помощью теоремы, обратной к теореме Пифагора, можно по длинам сторон определить, является он прямоугольным или нет.
Наиболее интересны прямоугольные треугольники с целочисленными длинами сторон. Так, например, треугольники
3, 4, 5 и далее им подобные 6, 8, 10, далее 9, 12, 15 и т.д.
5, 12, 13 и далее им подобные 10, 24, 26 и т.д.
8, 15, 17 и далее им подобные.
7, 24, 25 и далее им подобные.
Скорее всего таких независимых серий прямоугольных треугольников с целочисленными длинами сторон бесконечно много.
 
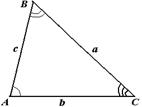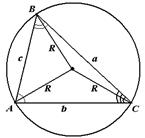
| Теорема 26. (синусов) Стороны треугольника пропорциональны синусам противолежащих углов. 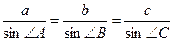 . Следствием к теореме синусов можно считать следующую теорему. Теорема 27. Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника..  .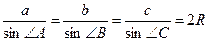
|
|
| Теорема 28. (косинусов) Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.  .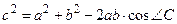
|
4. Як відомо, медианами трикутника називаються відрізки, що з'єднують його вершини з серединами протилежних сторін. Всі три медіани перетинаються в одній точці і діляться нею у відношенні 1:2.
Точка перетину медіан є також центром ваги трикутника. Якщо підвісити картонний трикутник в точці перетину його медіан то він буде перебувати в стані рівноваги
Цікаво, що вcе шість трикутників, на які кожен трикутник розбивається своїми медианами, мають однакові площі.
Медіани трикутника через його боку виражаються так:
,
,
.
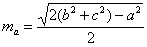
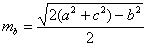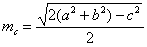Якщо дві медіани перпендикулярні, то сума квадратів сторін, на які вони опущені, в 5 разів більше квадрата третьої сторони.
Побудуємо трикутник, сторони якого рівні медианам даного трикутника, тоді медіани побудованого трикутника будуть рівні 3 / 4 сторін початкового трикутника.
Даний трикутник назвемо першим, трикутник з його медіан - другим, трикутник з медіан другого - третім і т. д. Тоді трикутники з непарними номерами (1,3, 5, 7 ,...) подібні між собою і трикутники з парними номерами ( 2, 4, 6, 8 ,...) також подібні між собою.
Сума квадратів довжин всіх медіан трикутника дорівнює ¾ суми квадратів довжин його сторін.
5. Трикутник є найпростішою геометричною фігурою, тому відомо багато теорем про його елементи, одним із яких є бісектриса.
Бісектриса трикутника — це відрізок бісектриси одного з кутів цього трикутника від вершини кута до точки перетину з протилежною стороною.
Бісектриси трикутника перетинаються в одній точці — в центрі вписаного в трикутник кола.
Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам, а саме на відрізки, відношення яких дорівнює відповідно відношенню прилеглих до них двох інших сторін трикутника.
Або бісектриса трикутника розбиває деяку сторону на дві такі частини, що відношення однієї з них до прилеглої до неї сторони трикутника дорівнює відношенню другої частини до відповідно прилеглої до неї сторони трикутника.
Корисними при розв’язанні задач є властивості елементів прямокутного трикутника.
6. Висота трикутника, опущена з даної вершини, — це перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника.
У кожному трикутнику можна провести три висоти. У гострокутному трикутнику всі висоти лежать усередині трикутника.
У тупокутному трикутнику висоти, проведені з вершин гострих кутів, лежать зовні трикутника.
У прямокутному трикутнику висоти, проведені з вершин гострих кутів, збігаються з його сторонами.
Точка перетину висот трикутника називається його ортоцентром. У гострокутному трикутнику ортоцентр лежить усередині трикутника. У прямокутному — у вершині прямого кута, у тупокутному трикутнику — поза трикутником.
7. Коло дев'яти точок і пряма Ейлера
Розглянемо довільний трикутник. Теорема Ейлера про коло дев'яти точок говорить: основи висот, середини сторін і середини відрізків, що з'єднують ортоцентр - точку перетину висот - з вершинами трикутника, лежать на одному колі - колі дев'яти точок.
При гомотетії с центром в ортоцентрі трикутника і коеффіцієнтом 1/2 описане коло навколо трикутника переходить в коло дев*яти точок.
При цій гомотетії центр описаного кола переходить в центр кола дев*яти точок.Отже, центр кола дев*яти точок — середина відрізкака, що з*єднує ортоцентр трикутника с центром його описаного кола.
При гомотетии з центром в точці перетину медіан і коефіцієнтом -1/2 вершини трикутника переходять у середини протилежних сторін. Тому при цій гомотетії висоти переходять в серединні перпендикуляри, а ортоцентр - в центр описаного кола. Це означає, що центр ваги трикутника (точка перетину його медіан) лежить на відрізку, що з'єднує ортоцентр і центр описаного кола, і розташована вдвічі ближче до центру описаного кола, ніж до ортоцентру.
Таким чином, центр описаного кола, центр ваги, центр кола дев'яти точок і ортоцентр лежать на одній прямій - прямий Ейлера.
9. Великий клас чотирикутників становлять паралелограми.
Чотирикутник, у якого протилежні сторони паралельні, називається паралелограмом.
Висотою паралелограма називається відрізок, що є перпендикуляром до прямої, яка містить протилежну сторону.
У паралелограма з кожної його вершини можна провести по дві висоти. Висоти, проведені з вершин тупих кутів паралелограма, лежать у паралелограмі; висоти, проведені з гострих тупих кутів паралелограма, лежать зовні паралелограма.