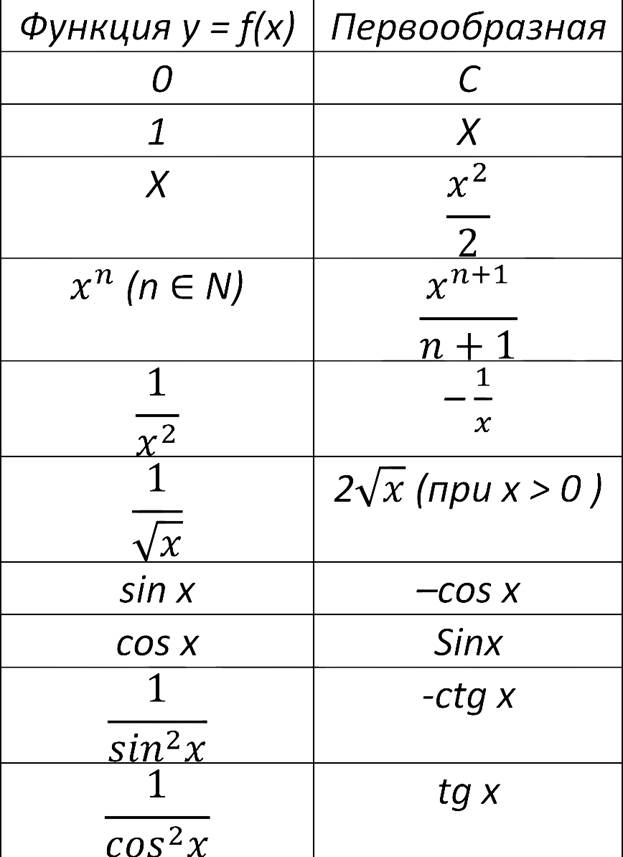Основное свойство первообразной
Первообразная и неопределенный интеграл.
Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка выполняется равенство
F'(x) = f(x) .
► Например, функция F(x) = х2 является первообразной для функции f(x) = 2х , так как
F'(x) = (х2)' = 2x = f(x). ◄
Основное свойство первообразной
Если F(x) — первообразная для функции f(x) на заданном промежутке, то функция f(x) имеет бесконечно много первообразных, и все эти первообразные можно записать в виде F(x) + С, где С — произвольная постоянная.
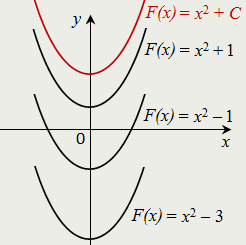
| ► Например. Функция F(x) = х2 + 1 является первообразной для функции f(x) = 2х, так как F'(x) = (х2 + 1)' = 2x = f(x); функция F(x) = х2 – 1 является первообразной для функции f(x) = 2х , так как F'(x) = (х2 – 1)' = 2x = f(x); функция F(x) = х2 – 3 является первообразной для функции f(x) = 2х , так как F'(x) = (х2 –3)' = 2x = f(x) ; любая функция F(x) = х2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х. ◄ |
Правила вычисления первообразных
1. Если F(x) — первообразная для f(x), а G(x) — первообразная для g(x), то F(x) + G(x) — первообразная для f(x) + g(x). Иными словами, первообразная суммы равна сумме первообразных.
2. Если F(x) — первообразная для f(x), и k — постоянная, то k·F(x) — первообразная для k·f(x). Иными словами, постоянный множитель можно выносить за знак производной.
3. Если F(x) — первообразная для f(x), и k, b — постоянные, причём k ≠ 0, то 1/k · F(kx + b) — первообразная для f(kx + b).
Неопределённый интеграл
Неопределённым интегралом от функции f(x) называется выражение F(x) + С, то есть совокупность всех первообразных данной функции f(x). Обозначается неопределённый интеграл так:
∫ f(x) dx = F(x) + С,
где
f(x) — называют подынтегральной функцией;
f(x) dx — называют подынтегральным выражением;
x — называют переменной интегрирования;
F(x) — одна из первообразных функции f(x);
С — произвольная постоянная.
► Например, ∫ 2x dx = х2 + С, ∫ cos x dx = sin х + С и так далее. ◄
Слово "интеграл" происходит от латинского слова integer, что означает "восстановленный". Считая неопределённый интеграл от 2x, мы как бы восстанавливаем функцию х2, производная которой равна 2x. Восстановление функции по её производной, или, что то же, отыскание неопределённого интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию.Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Основные свойства неопределённого интеграла
1. Производная неопределённого интеграла равна подынтегральной функции:
(∫ f(x) dx)' = f(x).
2. Постоянный множитель подынтегрального выражения можно выносить за знак интеграла:
∫ k · f(x) dx = k · ∫ f(x) dx.
3. Интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций:
∫ (f(x) ± g(x)) dx = ∫ f(x) dx ± ∫ g(x) dx.
4. Если k, b — постоянные, причём k ≠ 0, то
∫ f(kx + b) dx = 1/k · F(kx + b) + С.
Таблица первообразных и неопределённых интегралов