Тема СРС: Условный оператор.

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Количество часов: 3.

 

ЗАДАНИЕ. Выполнить постановку задачи, составить алгоритм и написать программу с использованием условного оператора.

 

Вариант Задание
1. На шахматной доске стоят черный король и белые ладья и слон (ладья бьет по горизонтали и вертикали, слон — по диагоналям). Проверить, есть ли угроза королю и если есть, то от кого именно. Учесть возможность защиты (например, ладья не бьет через слона). Позицию каждой шахматной фигуры или шашки можно задавать в обычной нотации (например, d7) или парой чисел — координат фигуры (например, 4;7).
2. Вычислить значение функции: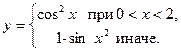
3. Дано четыре числа. Найти наибольшее из них.
4. Даны три вещественных числа. Определить, могут ли они являться длинами сторон некоторого треугольника. У треугольника длина любой стороны меньше суммы длин двух других.
5. Для заданного n вывести фразу вида: «21 год», «32 года», «12 лет».
6. Можно ехать на такси со скоростью v1 км/ч и оплатой р1 тг/км либо идти пешком со скоростью v2 км/ч бесплатно. Как с наименьшими затратами преодолеть путь s за время t, если это возможно? Каковы эти затраты?
7. Даны три целых числа, определяющих некоторую дату (не ранее 1600 г.). Определить дату завтрашнего дня.
8. Вычислить значение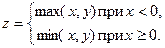
9. Пройдет ли кирпич со сторонами a, b и с сквозь прямоугольное отверстие со сторонами r и s? Стороны отверстия должны быть параллельны граням кирпича.
10. Вычислить значение функции:
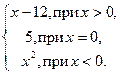
11. Можно ли коробку размером a´b´c упаковать в посылку размером r´s´t? «Углом» укладывать нельзя.
12. Значения переменных x, y и z поменять местами так, чтобы оказалось x ≥ y ≥ z.
13. По номеру некоторого года определить номер его столетия (учесть, что, к примеру, началом ХХ столетия был 1901 год, а не 1900 год).
14. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Проверить этот признак на примере заданного трехзначного числа.

 

 

Краткий конспект лекции №14