Тема лабораторного занятия: Условный оператор.

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Количество часов: 2.

 

Напишите и выполните следующие готовые программы на языке Паскаль.

Упражнение 1. Задача. Определить положительно введенное целое число или нет. Program pos; var n : integer; begin clrscr; readln(n); if (n > 0) then writeln ('Переменная n положительна') else writeln ('Переменная n не положительна'); readln; end.   77 Упражнение 2. Задача. Определить максимальное из двух чисел. PROGRAM max_ab; uses crt;{подключение модуля CRT} var a,b,max : integer; begin clrscr; {процедура очистки экрана} write('a='); readln(a); {ввод значения переменной а} write('b='); readln(b); {ввод значения переменной b} if a>b then max:=a else max:=b; writeln(’maximum ’,a,’ and ’,b,’ is ’,max); readln; {Задержка экрана} end.  
Упражнение 3. Задача. Определить максимальное из трех чисел. PROGRAM max_abс; uses crt;{подключение модуля CRT} var a,b,c,max : integer; begin clrscr; write('a='); readln(a); write('b='); readln(b); write('с='); readln(с); if a>b then max:=a else max:=b; if c>max then max:=c; writeln(’maximum ’,a,’, ’,b,’ and ’,c,’ is ’,max); readln; {Задержка экрана} end.   Упражнение 4. Задача. Найти значение функции signx. Функция signx определяется так: 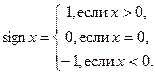PROGRAM signum; uses crt;{подключение модуля CRT} const m=5; n=2; var x,sign:real ; begin clrscr; write('x='); readln(a); if x>0 then sign:=1 {x>0} else if x=0 then sign:=0 {x=0} else sign:=-1; {x<0} writeln(’sign(’,x:m:n,’)=’,sign:m:n); readln; {Задержка экрана} end.  


Методические рекомендации по СРСП №13

Тема: Условный оператор.

Количество часов: 3.

 

Задание. Составить алгоритмы и написать программы с использованием условного оператора для решения следующих задач.

 

Вариант Задание
1. Известно, что из четырех чисел а1, а2, а3 и а4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.
2. Суточный рацион коровы составляет u кг сена, v кг силоса и w кг комбикорма. В хозяйстве, содержащем стадо из k голов, осталось s центнеров сена, t тонн силоса и f мешков комбикорма по 50 кг. Сколько еще дней хозяйство сможет кормить коров по полному рациону? Какой из кормов кончится раньше других?
3. Дано четыре числа. Найти наименьшее из них.
4. Дан номер года. Определить количество дней в этом году. Указание. Високосным считается год, номер которого кратен четырем. Исключение составляют годы, номера которых кратны 100, а число сотен у номеров не делится на 4: 1700, 1800, 1900, 2100 и т.д.
5. Даны две целочисленные переменные m и n. Если оба значения кратны 3, то вычислить их сумму, в противном случае – разность.
6. Составить программу, определяющую, принадлежит ли точка х одному из отрезков [2, 5] или [-1, 1].
7. Переменной k присвоить номер четверти плоскости, в которой точка с координатами х и у (ху ≠ 0) Если ху = 0, то вывести сообщение, что точка лежит на одной из осей координат.
8. Решить уравнение ax + b = 0. Указание. В математике под словосочетанием «решить уравнение» понимается нахождение множества ВСЕХ корней уравнения. Это множество может быть: - пустым (Æ); - состоять из конечного числа элементов; - бесконечным (R — множество всех действительных чисел, отрезок [0,1] и т.п.). При решении уравнения ax + b = 0 рассматриваются три случая: 1) a ¹ 0 — уравнение имеет единственный корень. Какой? 2) a = 0, b=0. Ответ: R — вся числовая прямая. 3) a = 0, b ≠ 0. Ответ: Æ.
9. Вычислить значение функции:
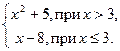
10. Решить квадратное уравнение ax2+bx+c=0. Рассмотреть все случаи (в зависимости от коэффициента a и дискриминанта).
11. Если значение переменной х не равно 0 и при этом котангенс от х меньше 0,5, тогда поменять знак у х, а если значение х равно 0, тогда присвоить х значение 1.
12. Перераспределить значения двух переменных х и у так, чтобы в х оказалось большее из этих значений, а в у — меньшее.
13. Написать программу, моделирующую работу кассира в магазине. Программа должна запрашивать стоимость покупки, сумму денег, внесенную покупателем, далее определяет причитающуюся сдачу (если денег внесено больше), печатает СПАСИБО, если сдачи не требуется, или выдает сообщение о недостаточности внесенной суммы.

 

Методические рекомендации по СРС №13