Перечень вопросов, рассматриваемых в теме

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Первообразная.

Конспект урока

Перечень вопросов, рассматриваемых в теме

1) Нахождение первообразной

2) Определение первообразной, график которой проходит через заданную точку

3) Решение задач, обратных задаче нахождения закона изменения скорости материальной точки по закону ее движения

Глоссарий по теме

Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для 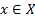выполняется равенство F’ (x) = f(x).

Таблица первообразных:

Функция f(x)	Первообразная F(x)
0	C = const
1	x + C
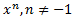
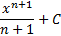
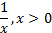
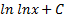
cos x	sin x + C
sin x	-cos x + C

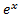
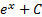
Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Сегодня мы познакомимся с новым математическим понятием – первообразной. Что это такое?

Для начала обратимся к задаче, которая поможет сформулировать определение первообразной.

С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени. Если некоторая точка прошла путь S(t), то ее мгновенная скорость 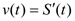. Если теперь рассмотреть обратную задачу – нахождение пути, пройденного точкой с заданной скоростью, то придем к функции S(t), которую называют первообразной функции v(t), т.е. такой функцией, что .

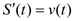Итак, функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для х 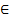Х выполняется равенство F’ (x) = f(x).

Как следует из определения, операция нахождения первообразной – обратна нахождению производной функции.

Свойство первообразных

• Если F(x) — первообразная для функции f(x) на заданном промежутке, то функция f(x) имеет бесконечно много первообразных, и все эти первообразные можно записать в виде F(x) + С, где С — произвольная постоянная.

Геометрическая интерпретация

• Графики всех первообразных данной функции f (x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.

Правила вычисления первообразных

1. Первообразная суммы равна сумме первообразных. Если F(x) — первообразная для f(x), а G(x) — первообразная для g(x), то F(x) + G(x) — первообразная для f(x) + g(x).

2. Постоянный множитель можно выносить за знак производной. Если F(x) — первообразная для f(x), и k — постоянная, то k·F(x) — первообразная для k·f(x).

3. Если F(x) — первообразная для f(x), и k, b — постоянные, причём k ≠ 0, то 1/k · F(kx + b) — первообразная для f(kx + b).

Запомни!

Любая функция F(x) = х ² + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

• Например:

F'(x) = (х² + 1)' = 2x = f(x);

f(x) = 2х , т.к. F'(x) = (х² – 1)' = 2x = f(x);

f(x) = 2х , т.к. F'(x) = (х² –3)' = 2x = f(x);