Тема СРСП: Составление алгоритма и представление его в виде блок-схемы.
Количество часов: 3.
Задание. Для каждой задачи выполните постановку, выберите метод решения, составьте алгоритм в словесной и графической формах, проведите анализ полученных результатов. Алгоритм первой задачи содержит только линейную конструкцию, а в алгоритм второй задачи должна присутствовать разветвляющаяся. Блок-схему лучше составить в конструкторе блок-схем Flowcharts для определения правильности работы алгоритма.
| Вариант | Задание |
| 1. | 1. Пушка стреляет под углом α° к линии горизонта. Начальная скорость снаряда — v0 м/с. Найти дальность и время полета снаряда.
Указание. 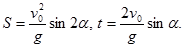 2. Дано четыре числа. Найти наибольшее из них.
2. Дано четыре числа. Найти наибольшее из них.
|
| 2. | 1. В такси одновременно сели три пассажира. Когда вышел первый пассажир, на счетчике было р1 тенге; когда вышел второй — р2 тенге. Сколько должен заплатить каждый пассажир, если по окончанию поездки счетчик показал р3 тенге? Указание. Каждый пассажир должен заплатить пропорционально расстоянию, которое он проехал. Например, пусть р1=100, р2=200, р3=300. Тогда первый пассажир должен заплатить 50 тенге, второй — 100 тенге, третий —150 тенге. Все вместе заплатят 50+100+150 = 300 = р3. 2. Дано четыре числа. Найти наименьшее из них. |
| 3. | 1. Вычислить площадь треугольника, если известны три его стороны.
Указание. 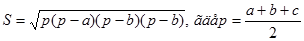 . В конструкторе блок-схем . В конструкторе блок-схем 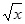 записывается как sqrt(x).
2. Даны три вещественных числа. Определить, могут ли они являться длинами сторон некоторого треугольника.
Указание. У треугольника длина любой стороны меньше суммы длин двух других. записывается как sqrt(x).
2. Даны три вещественных числа. Определить, могут ли они являться длинами сторон некоторого треугольника.
Указание. У треугольника длина любой стороны меньше суммы длин двух других.
|
| 4. | 1. Известны: сумма в тенге и сумма в долларах. Осуществить перевод из долларов тенге и из тенге в доллары по известным курсам продажи и покупки доллара. Указание. Курс продажи доллара — это тот курс, по которому нам продают валюту, курс покупки — курс, по которому валюту покупают у нас. Курс покупки всегда меньше курса продажи. 2. Составить программу, определяющую, принадлежит ли точка х одному из отрезков [2; 5] или [-1; 1]. |
| 5. | 1. Найти среднее арифметическое трех чисел. 2. Решить уравнение ax + b = 0. Напомним, что решить уравнение — значит найти множество ВСЕХ его корней. Это множество может быть пустым, состоять из одного, двух или более элементов. Оно может быть и бесконечным. Для данного уравнения следует рассмотреть все возможные случаи в зависимости от того, равен или не равен нулю старший коэффициент а. Если a ¹ 0, то уравнение имеет единственный корень. Какой? Если a = 0, то следует рассмотреть еще два варианта: когда b равен нулю и когда не равен нулю. |
| 6. | 1. Автомобиль проехал S1 км со скоростью v1 км/ч, S2 км со скоростью v2 км/ч, S3 км со скоростью v3 км/ч. Найти среднюю скорость на всем пути. vср = 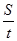 , где S —полный путь, t — время, затраченное на весь путь.
2. Решить уравнение ax2 + bx + c = 0. Рассмотреть все случаи (в зависимости от коэффициента a и дискриминанта). , где S —полный путь, t — время, затраченное на весь путь.
2. Решить уравнение ax2 + bx + c = 0. Рассмотреть все случаи (в зависимости от коэффициента a и дискриминанта).
|
| 7. | 1. Треугольник задается координатами своих вершин на плоскости: А(х1,у1), В(х2,у2), С(х3,у3). Найти сумму длин медиан треугольника АВС.
Указание. Формулы координат середины отрезка: 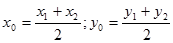 . Длина отрезка с координатами концов (х1, y1) и (x2, y2) находится по формуле . Длина отрезка с координатами концов (х1, y1) и (x2, y2) находится по формуле 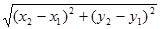 .
2. Вычислить значение функции: .
2. Вычислить значение функции:
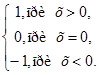
|
| 8. | 1. Вычислить площадь треугольника, если известны: сторона и высота, проведенная к ней. S = ah /2.
2. Вычислить значение функции:
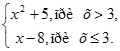
|
| 9. | 1. Угол α задан в градусах, минутах и секундах. Найти его величину в радианах. Решить задачу обратную предыдущей, то есть перевести заданную величину угла из радианной меры в градусную.
2. Вычислить значение функции:
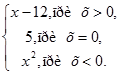
|
| 10. | 1. Дано: V — объем куба. Найдите длину ребра и площадь грани. 2. Составить алгоритм, моделирующий работу кассира в магазине. Программа должна запрашивать стоимость покупки, сумму денег, внесенную покупателем, далее определяет причитающуюся сдачу (если денег внесено больше), печатает СПАСИБО, если сдачи не требуется, или выдает сообщение о недостаточности внесенной суммы. |
| 11. | 1. Вычислить длину окружности, площадь круга и объем шара заданного радиуса. 2. Известно, что из четырех чисел а1, а2, а3 и а4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n. |
| 12. | 1. Вычислить площадь треугольника, если известны две стороны и угол между ними. S = ab sinÐС. 2. Даны две переменные x и у. Если значения обеих переменных больше 0, то переменной х присвоить значение квадратного корня из х, а переменной у — значение квадратного корня из у, иначе оба числа оставить прежними. |
Методические рекомендации по СРС №11
Тема: Составление алгоритма и представление его в виде блок-схемы.
Количество часов: 3.
Задание. Выполнить постановку задачи; выбрать метод решения; составить алгоритм в словесной и графической формах; провести анализ полученных результатов. Алгоритм задачи должен содержать циклическую конструкцию. Блок-схему лучше составить в конструкторе блок-схем для определения правильности работы алгоритма.
| Вариант | Задание |
| 1. | Дано n чисел. Найти наибольшее из них. |
| 2. | Дано n чисел. Найти наименьшее из них. |
| 3. | Дано n чисел. Найти их произведение. |
| 4. | Дано n чисел. Найти сумму положительных чисел. |
| 5. | Дано n чисел. Найти количество отрицательных чисел. |
| 6. | Дано n чисел. Найти наибольшее из отрицательных чисел. |
| 7. | Дано n чисел. Найти наименьшее из положительных чисел. |
| 8. | Найти значение n! = 1 × 2 × 3 × 4 × …× n. |
| 9. | Найти сумму первых n степеней двойки, начиная с нулевой степени: 1 + 2 + 4 + ... + 2n-1. |
| 10. | Найти сумму обратных величин первых n натуральных чисел: 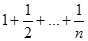 . .
|
| 11. | Найти сумму первых n натуральных нечетных чисел: 1+3+5+...+2n-1. |
| 12. | Найти сумму первых n натуральных четных чисел: 2 + 4 + 6 +...+ 2n. |
| 13. | Найти n-й член последовательности Фибоначчи, где f0 = f1 = 1, fn = fn-1 + fn-2 (n ³ 2). |
| 14. | Вычислить n-ю степень данного числа: xn =x×x×...×x. n — целое число.
Указание. x0 = 1. При n > 0 использовать рекуррентную формулу: xn = xn-1×x. При n < 0 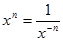 . .
|








