Тема: Постановка задачи. Составление алгоритма в виде блок-схемы.
Количество часов: 2.
линеЙныЕ алгоритмЫ
Упражнение 1
Задача. Найти сумму двух данных чисел.
Дано: a, b — слагаемые.
Требуется: sum — сумма значений а и b.
Метод решения: sum = a + b.
Словесная форма алгоритма:
Запросить значение переменной а
Запросить значение переменной b
Записать в переменную sum значение выражения a + b
Вывести значение переменной sum
Блок-схема:
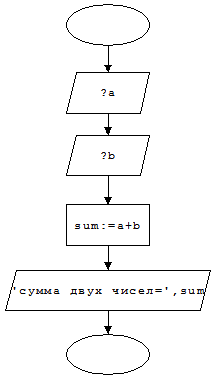
Анализ полученных результатов.
1. а = 4; b = 10. sum = 14.
2. а = –10; b = –11. sum = –21.
3. а = 45; b=10,5. sum=55,5.
Упражнение 2
Задача. Даны два числа, являющиеся величинами катетов некоторого прямоугольного треугольника. Вычислить длину гипотенузы этого треугольника.
Дано: x и y — катеты прямоугольного треугольника.
Требуется: z — гипотенуза прямоугольного треугольника.
Метод решения: z = 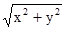 .
.
Словесная форма алгоритма:
Запросить значение переменной x
Запросить значение переменной y
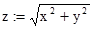 .
.
Вывести значение переменной z
Блок-схема:
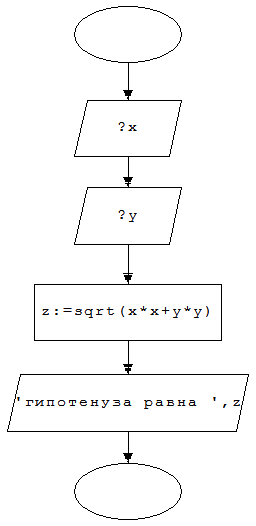
Анализ полученных результатов.
1. x = 3; y = 4. z = 5.
2. x = 11; y = 12. z = 16,28.
3. x = 25; y=30. z=39,05.
разветвляющиЕСЯ алгоритмЫ
упражнение 3
Задача. Найти максимум из двух чисел.
Дано: a, b — заданные числа.
Требуется: max — максимум из чисел а и b.
Метод решения: если a>b, то max присвоить a, иначе b.
Словесная форма записи алгоритма:
Запросить значение переменной a
Запросить значение переменной b
Если a>b, то max := a, иначе max:=b
Вывести значение переменной max
Блок-схема:
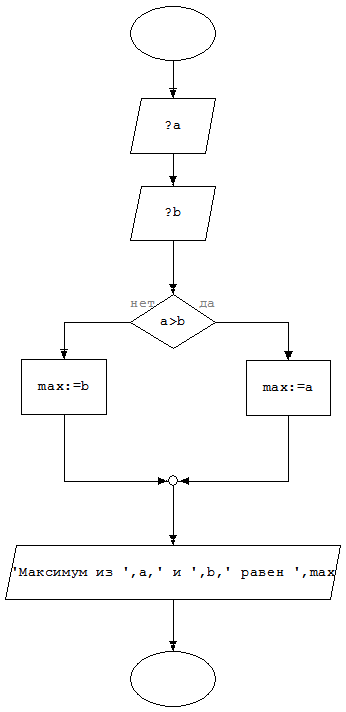
Анализ полученных результатов.
a = 3; b = 4. max = 4.
a = 11; b = 2. max =11.
a = 25; b=25. max =25.
Упражнение 4
Задача. Найти максимум из трех чисел.
Дано: Переменные a, b, с.
Требуется: max — максимум из чисел а, b, с.
Метод решения. Если a>b, то max:=a, иначе max:=b. Если c>max, то max:=c.
Словесная форма записи алгоритма:
Запросить значение переменной a
Запросить значение переменной b
Запросить значение переменной c
Если a>b, то max := a, иначе max := b
Если c>max, то max := c
Вывести значение переменной max
Блок-схема:
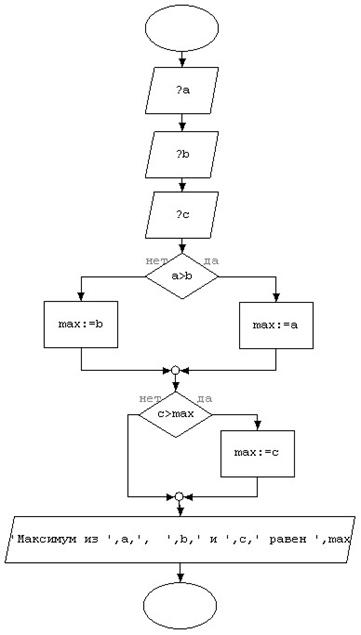
Анализ полученных результатов.
1. а = 4; b = 10; c = 4. max = 10.
2. а = –10; b = 12; c = 1. max = 12.
3. а = 45; b=10,5; c = 14. max=45.
циклическиЕ алгоритмЫ
Упражнение 5
Задача. Найти сумму первых n натуральных чисел.
Дано: n — количество первых натуральных чисел.
Требуется: S = 1 + 2 + …+ n — сумма первых n натуральных чисел.
Метод решения: Sn = Sn-1 + n.
Словесная форма записи алгоритма:
Запросить значение переменной n
i:=1
S:=0
Пока i<=n повторять
S := S+i
i := i+1
Конец цикла
Вывести значение переменной S
Блок-схема:
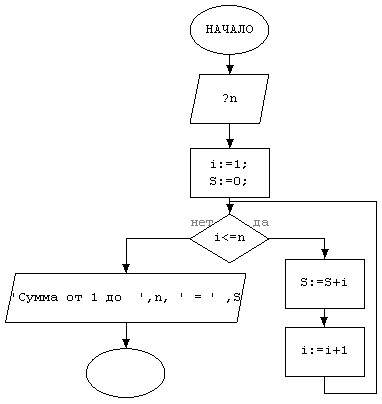
Тестирование алгоритма
Зададим количество суммируемых первых натуральных чисел n = 5. Мы должны получить значение суммы первых пяти натуральных чисел S = 15. Проведем трассировку алгоритма и запишем значения переменных i и S на каждом шаге в таблицу.
| До входа в цикл: | S:=0 | i:=1 | |||
| РАБОТА ЦИКЛА | |||||
| i на входе в тело цикла | Условие цикла | S | i на выходе из тела цикла | ||
| 1 | 1≤5 ? ДА | S:=S+i | 0+1 = 1® S | i:=i+1 | 1 +1 = 2 ® i |
| 2 | 2 ≤5 ? ДА | S:=S+i | 
| i:=i+1 | 
|
| 1+2 = 3® S | 2 +1 = 3 ® i | ||||
| 3 | 3 ≤5 ? ДА | S:=S+i | 
| i:=i+1 | 
|
| 3+3 = 6 ® S | 3 +1 = 4 ® i | ||||
| 4 | 4 ≤5 ? ДА | S:=S+i | 
| i:=i+1 | 
|
| 6+4 = 10® S | 4 +1 = 5 ® i | ||||
| 5 | 5 ≤5 ? ДА | S:=S+i | 
| i:=i+1 | 
|
| 10+5 = 15® S | 5 +1 = 6 ® i | ||||
| 6 | 6≤5? НЕТ | ВЫХОД ИЗ ЦИКЛА | |||
Упражнение 6
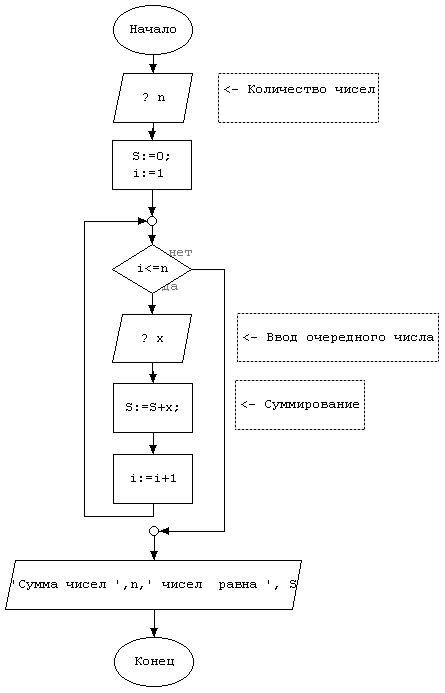
Задача. Дано n чисел. Найти их сумму.
Дано: n — количество чисел; х1, х2, ..., х n — числа, вводимые пользователем
Требуется: S = x1 + x2 + …+ xn — сумма n чисел.
Метод решения: Sn = Sn-1 + xn.
Отличие этой задачи от предыдущей состоит в том, что нам надо посчитать сумму чисел, которые вводятся пользователем. Ввод очередного числа будет осуществляться в новой итерации цикла. Введенное число будет прибавлено к имеющейся сумме.
Словесная форма записи алгоритма:
Запросить значение переменной n
i:=1
S:=0
Пока i<=n повторять
Запросить x
S := S+x
i := i+1
Конец цикла
Вывести значение переменной S
Блок-схема:
Методические рекомендации по СРСП №11








