10 Динамический расчет системы

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Этот расчет можно производить используя как МС так и МП

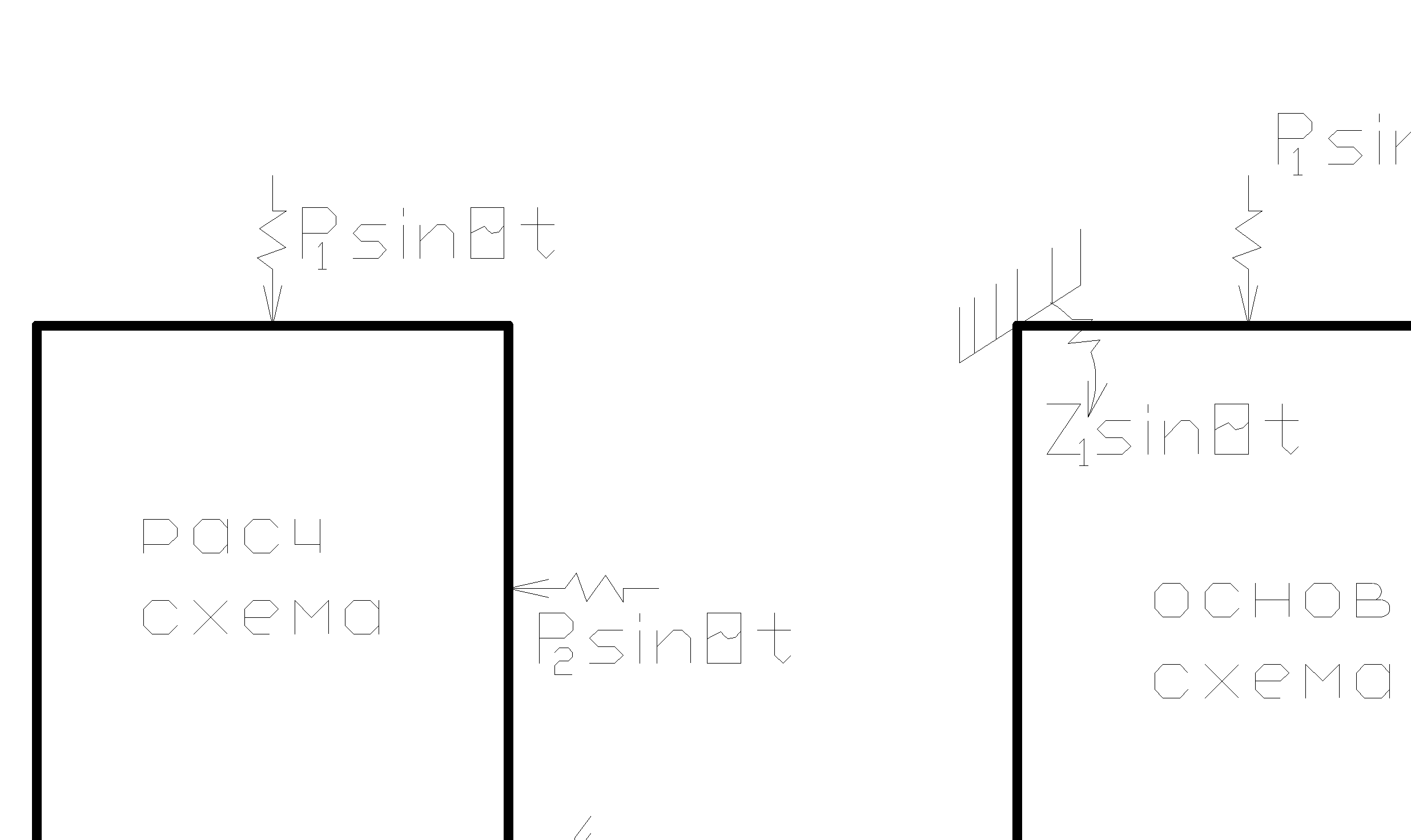
Основ сист задается путем наложения связей с одноврем динам неизвестн перемещ.

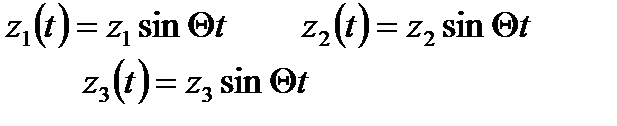
Канонич уравн-я

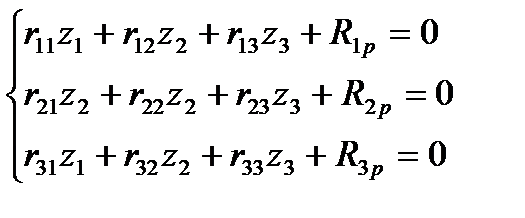
Неизвестные z1, z2, z3 – амплитуды вибрац перемещ. Коэф неизвестн-х – это амплитудные реакции связей от вибрационной нагрузки(т е при их определении учит силы инерции сосредоточенных или равномернораспред масс, стержней рамы). Для решения таких задач использ спец значения таких функций зависят от аргумента u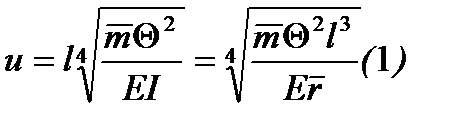

Где l – длина стержня, 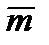- погонная масса стержня, EI- жесткость стержня, 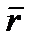- пол. жест. стер. q - частота вынужденных колебаний=частоте возмущ сил. При рассм собств колеб в формулу 1 вместо q®w (частота собственных колеб) В канон уравн свобод члены равны 0. Для получения Ур-я частот заставляют, прирав к 0 и раскрыв-ся определитель, сост-ий из клэф-ов при неизвестных канон уравн-ий. Окончат эпюра строиться по формуле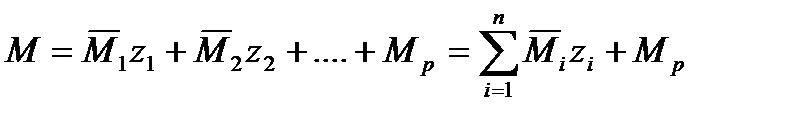

Расчет по МС:

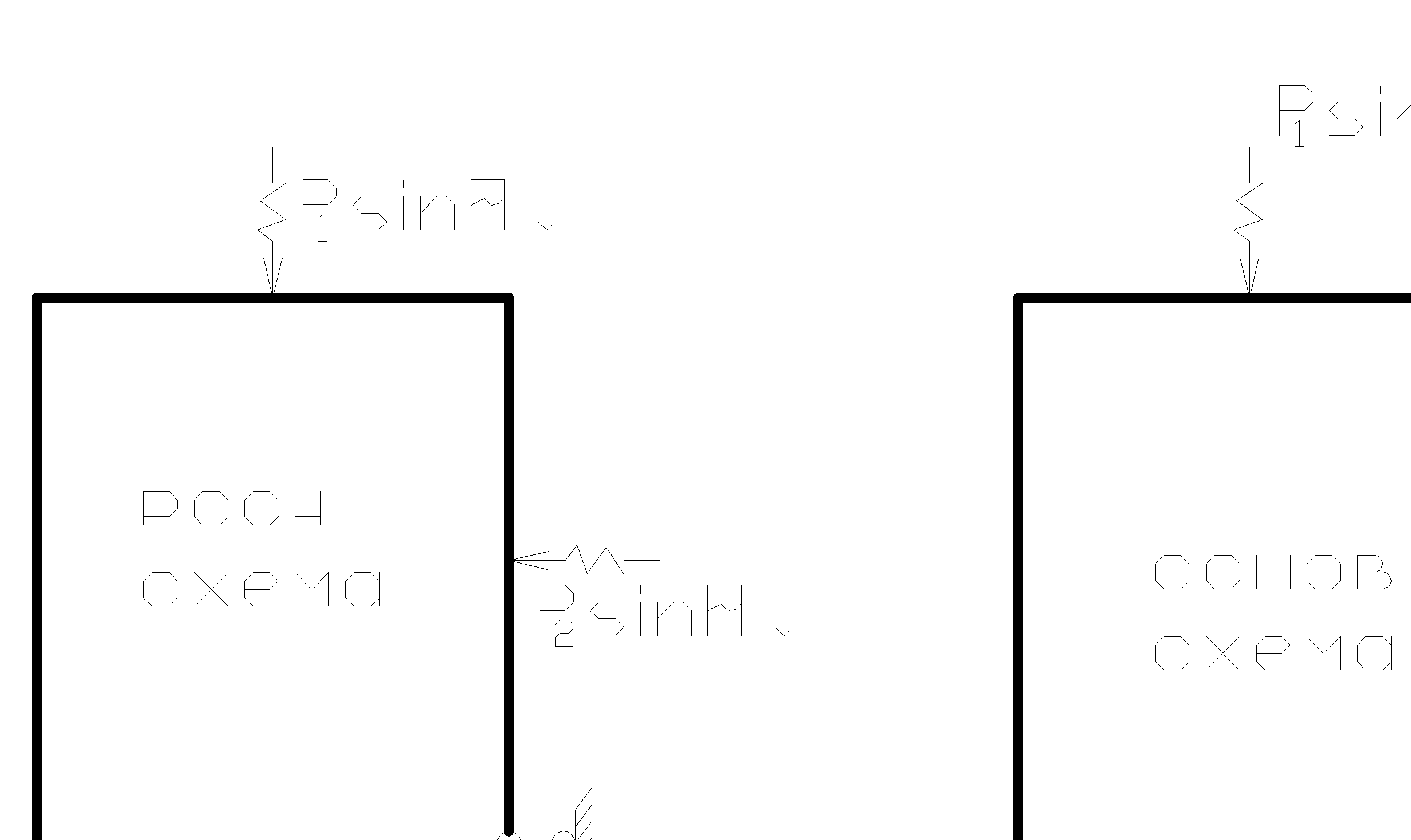
На сист действ вибрац гармонич нагрузки, q=const и наход в одной фазе. Заменим отброш связи неизвестн динамич реакциями, к-ые так же будут изменятся по тому же гармон закону к-му следует начальн нагр.

Канонич ур-ие, сокращаем sinqt

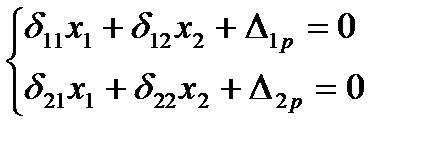
Где 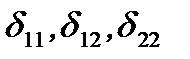амплитудные значения перемещений по направл неизвест от динам силы.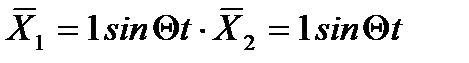

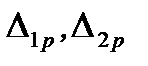- амплитудные перемещпо направл неизвест сил от динам нагрузки. Коэф при неизвест и свобод члены канон ур опред по формуле

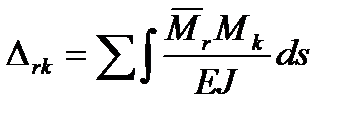где 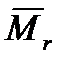- выражает момент от силы 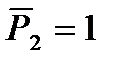, 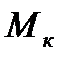-выраж изгиб момент, от динам нагрузки с учетом сил инерции, т к возник трудности с опред Мизг от динам нагрузки с учетом сил инерции, то МС мало эффект для динам рсчета рам. Для определ частот рсвобод колеб рам свобод члены канон ур приним =0, а вместо q берется w неизвест частот свобод колеб. Определитель из коэф системы прирав 0 и раскрывают. Это последнее уравн трансцендентное и сложное.Единств способ его нахожд – подбор.

 

 

8. Динамический расчет системы методом перемещений.

Основ сист задается путем наложения связей с одноврем динам неизвестн перемещ.

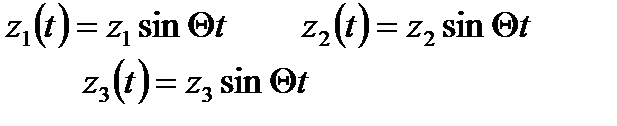
Канонич уравн-я

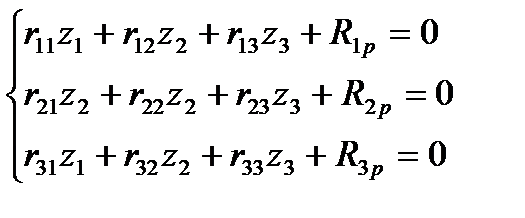
Неизвестные z1, z2, z3 – амплитуды вибрац перемещ. Коэф неизвестн-х – это амплитудные реакции связей от вибрационной нагрузки(т е при их определении учит силы инерции сосредоточенных или равномернораспред масс, стержней рамы). Для решения таких задач использ спец значения таких функций зависят от аргумента u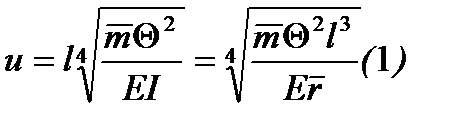

Где l – длина стержня, 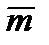- погонная масса стержня, EI- жесткость стержня, 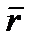- пол. жест. стер. q - частота вынужденных колебаний=частоте возмущ сил. При рассм собств колеб в формулу 1 вместо q®w (частота собственных колеб) В канон уравн свобод члены равны 0. Для получения Ур-я частот заставляют, прирав к 0 и раскрыв-ся определитель, сост-ий из клэф-ов при неизвестных канон уравн-ий. Окончат эпюра строиться по формуле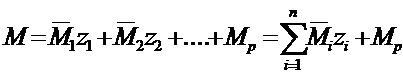

8. Динамический расчет системы методом перемещений.

Порядок расчета:1. Анализируем схему и выбираем основную систему.2. Строится изгибающий момент.

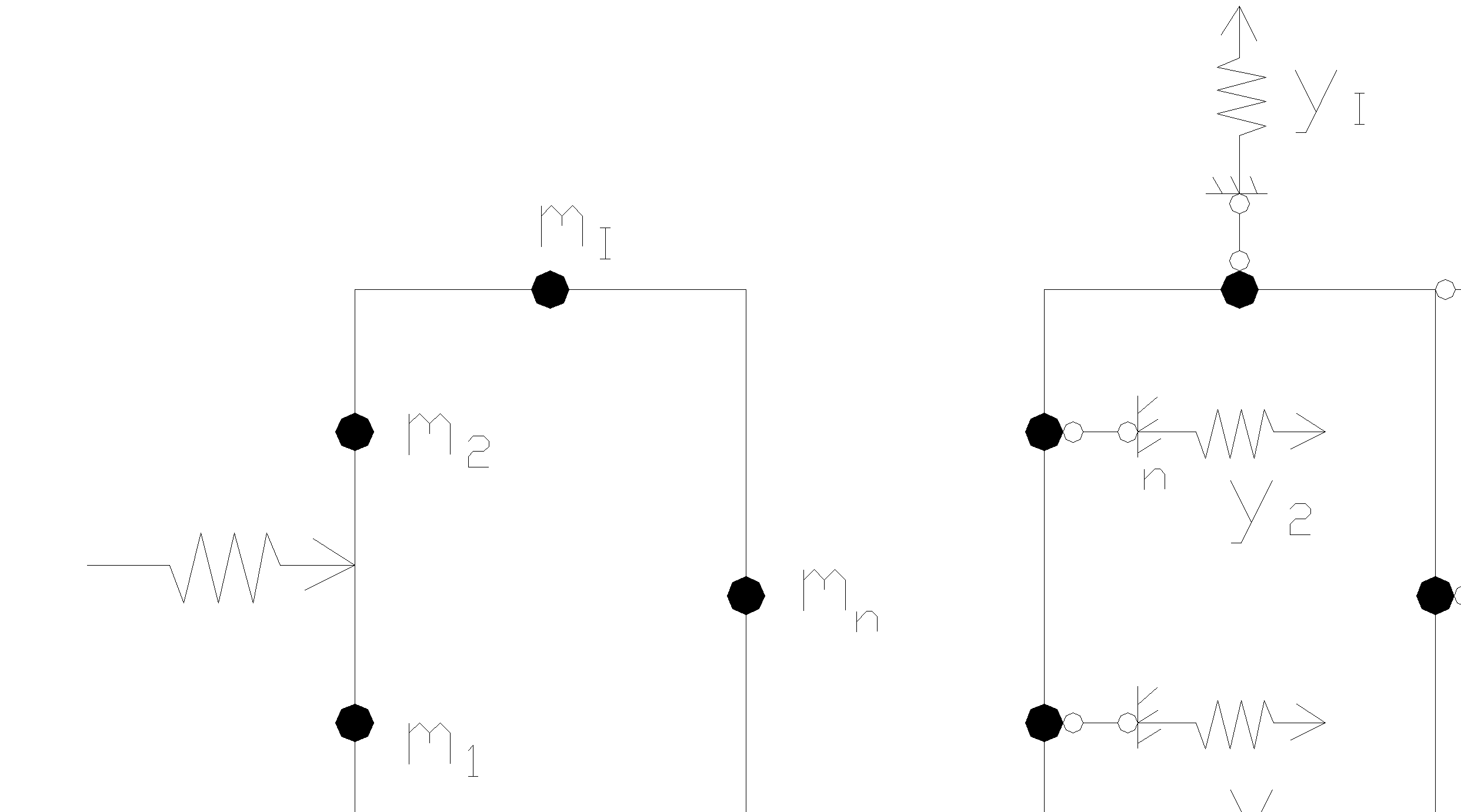
Для заданной системы основная получилась путем введения связей по направлению неизвестных перемещений z1, z2 … zn cсоответствующих масс m1, m2 …mn. число степеней свободы упругой системы определяется числом возможных независимых смещений. Получаем систему уравнений: 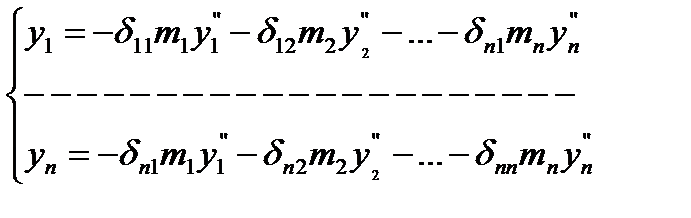(1)

Частное решение системы:

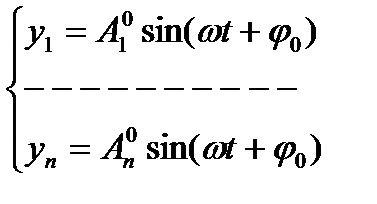(2)

A1, An – амплитуды колебаний соотв. масс, φ0 – нач. фаза колебаний.Возьмем вторую производную по времени t:

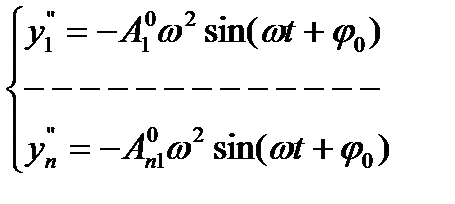(3)

Подставляем из ур-я (3) и (2)в (1):

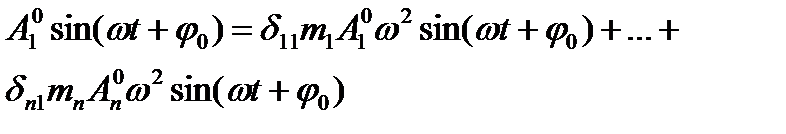
Перобразовываем:

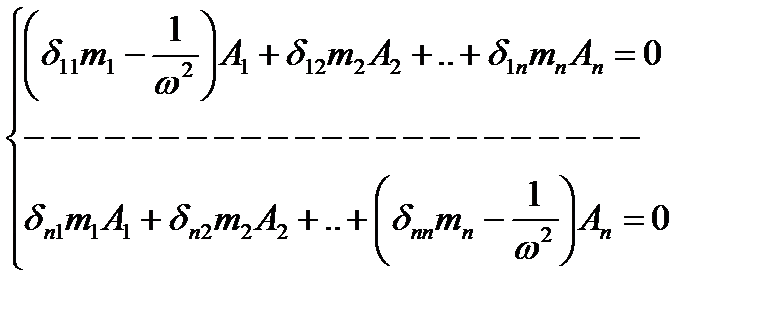
1/ω2=λ

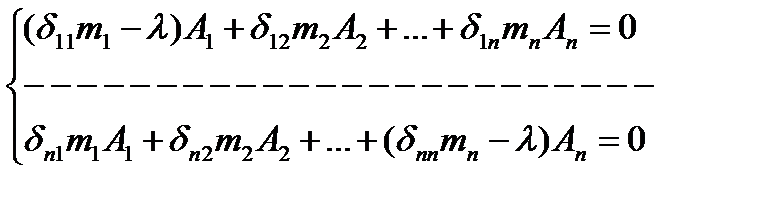
Если А1=А2=…=Аn=0 (сист-ма наход. в покое) Если А1≠А2≠Аn, тогда когда определитель из коэф-ов при амплитудах=0.

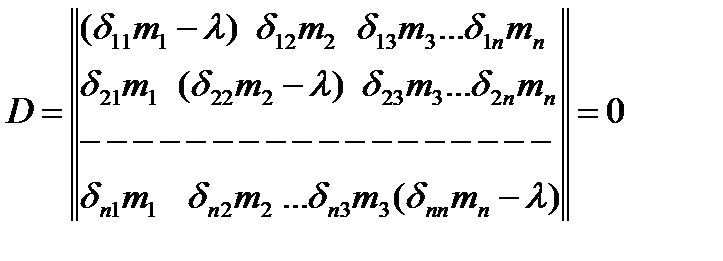
Вековое ур-ие с n-степенью свободы. Раскрываем полученный определитель. Если вековое уравнение 2-го или 3-го порядка его решение достаточно просто, но при дальнейшем увеличении порядка решение становится затруднительным.