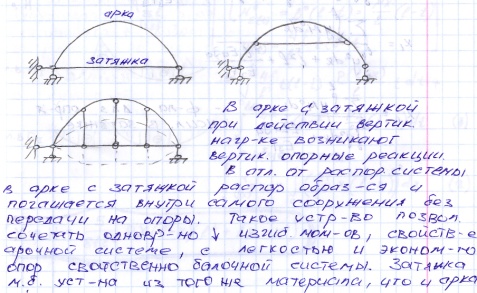
9, 27 Расчет двухшарнирной арки с затяжкой
ВНИЗУ НЕТ
9, 27 Расчет двухшарнирной арки с затяжкой
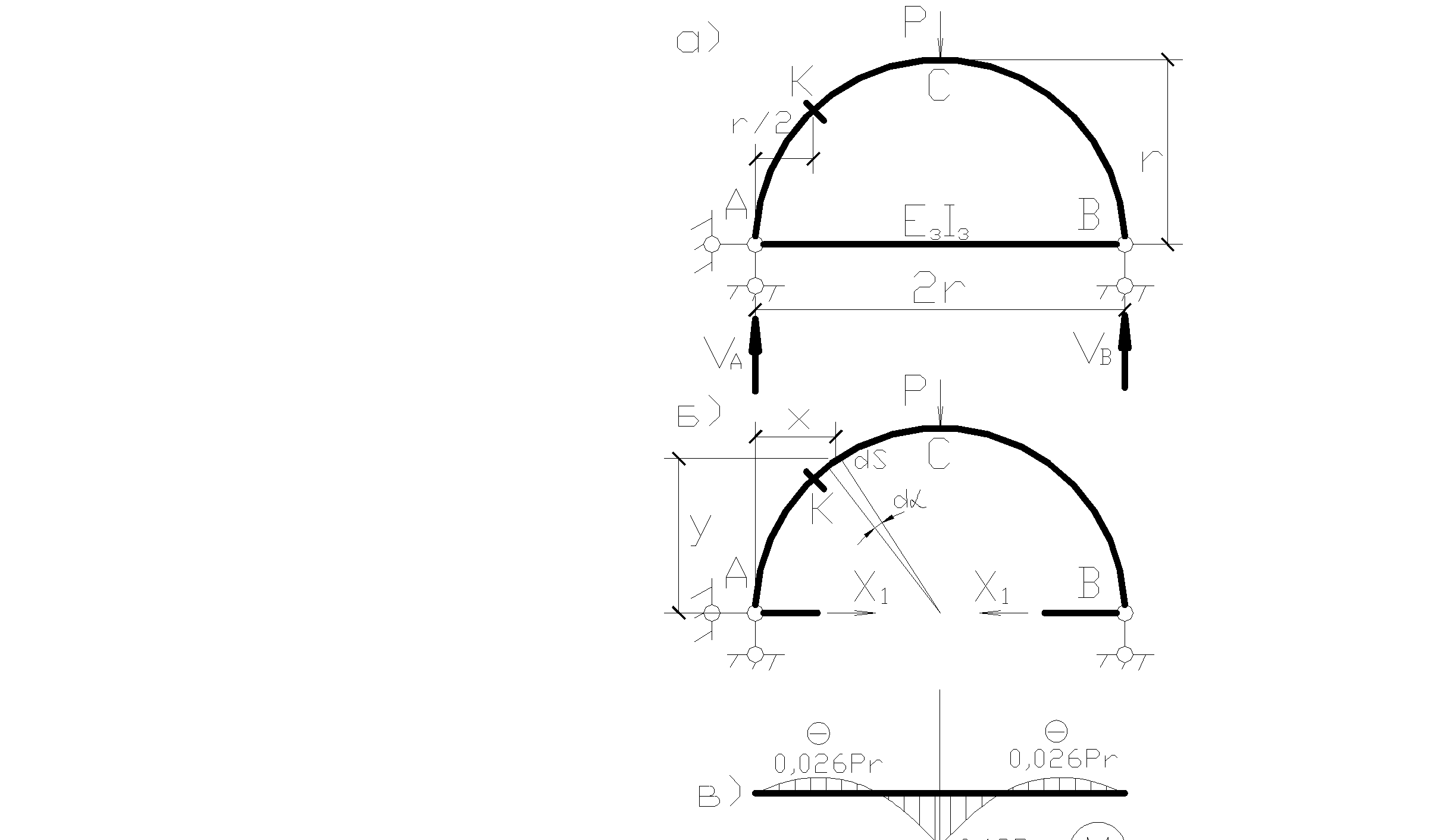
Построим эпюры изгибающих моментов в сечении арки. Влиянием продольной и поперечной силы в арке пренебрегаем. Сечение арки постоянно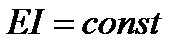 
сечение затяжки 
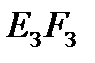. Выбираем основную систему. Для этого разрежем затяжку и приложим в этом месте силу X.
Так как ось арки представляет собой половину окружности, поэтому переходим к полярным координатам.
.
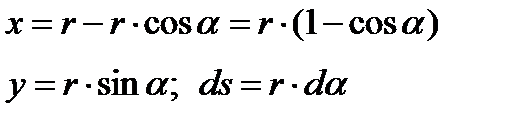Выражение для изгибающего момента в основной системе отдельно от силы P и отдельно от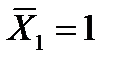 
:
.
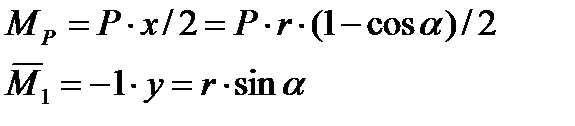Переходим к определению перемещени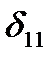й 
и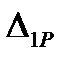 
. При определении перемещений 
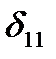учитывают деформации арки от изгиба и затяжки от растяжения:
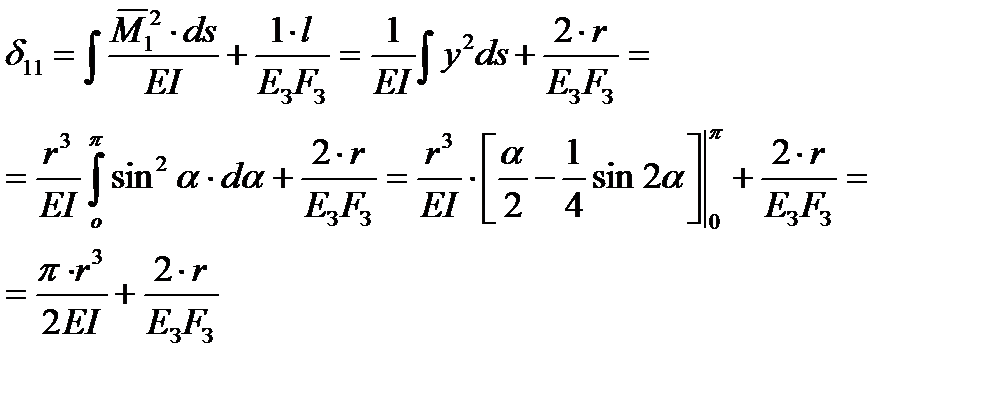При определении перемещения 
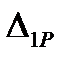учитываются только деформации арки от изгиба:
.
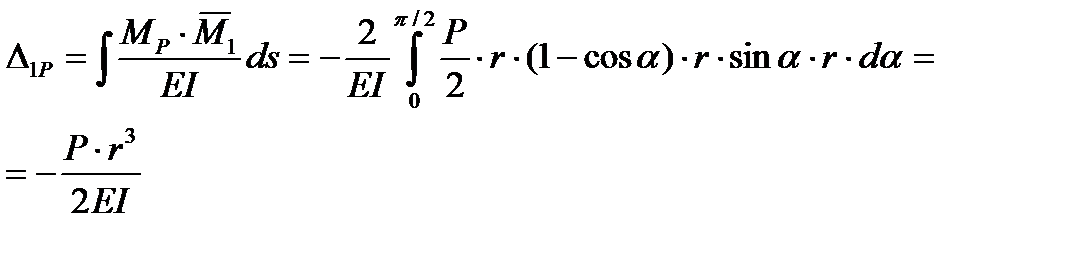Усилие в затяжке или распор:
.
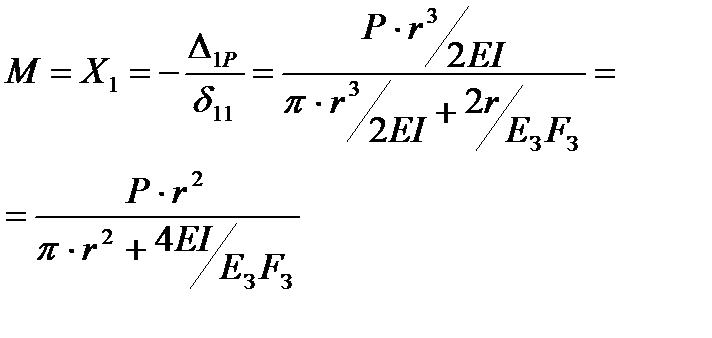Значение распора H в арках с затяжкой зависит от жесткости затяжки с увеличением жесткости затяжки распор возрастает. Значение изгибающего момента в арке с затяжкой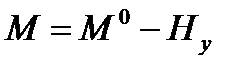 
, также зависит от жесткости затяжки. С увеличением жесткости затяжки положительные моменты в арке уменьшаются и наоборот.
Если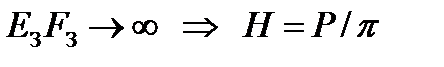 
- эпюра в), если 
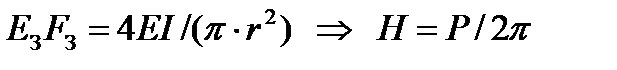- эпюра г).
11. Применение уравнений 3-х моментов для расчёта неразрезных балок.
В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:
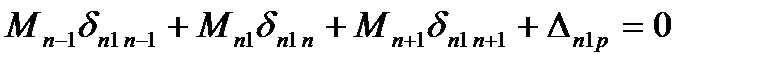
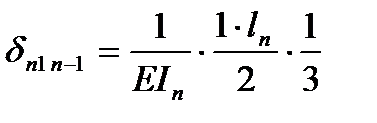
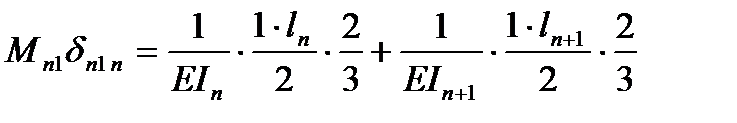
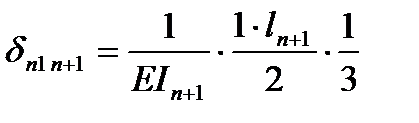
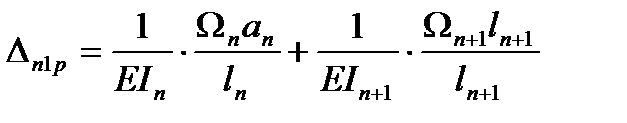
Подставляем: ……
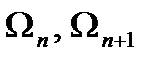- площади эпюр моментов;
an , bn+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EIc получаем:
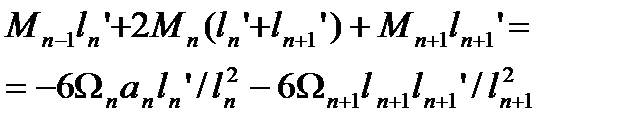
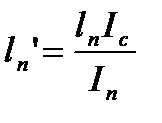
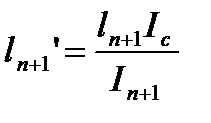
Уравнение 3-х моментов в общем виде. Если I=const
В уравнениях неизвестными являются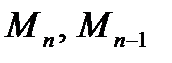 
т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:
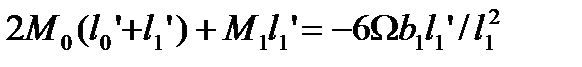
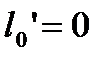
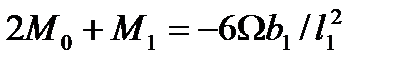
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца: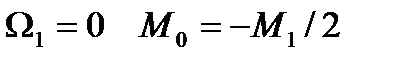 
12, 48 Вынужденные колебания системы с конечным числом степеней свободы
