6. Методы исследования устойчивости упругих систем

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1 Расчет рам методом сил на действие температуры и смещение опор. При изменении 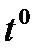в статически неопределимых системах все элементы работают в пределах упругих деформаций от совокупности нагрузок и температуры, при этом в конструкции возникают внутренние усилия. Температурные перемещения в статически определимых системах совершаются свободно и, следовательно, не возбуждают никаких напряжений или усилий. При равномерном нагревании прямолинейного стержня он искривляется без изгибающих напряжений.

При расчете рам на тепловое воздействие и на смещение опор переход к основной системе осуществляется также как и при расчете на силовое воздействие. Аналогично вычисляют и проверяют коэффициенты при неизвестных в канонических уравнениях. Системы канонических уравнений подобны с той разницей, что в качестве свободных членов вместо 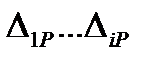должны быть поставлены 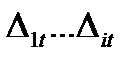при расчете рам на тепловое воздействие, 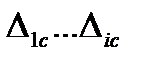при расчете на смещение опор.

Свободные члены вычисляют:

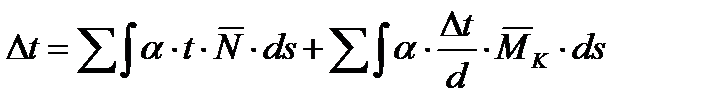, где

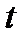- температура от действия равномерного нагрева;

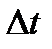- разница температур при неравномерном нагреве ( 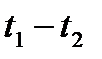).Проверка свободных членов:

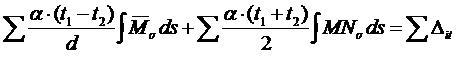
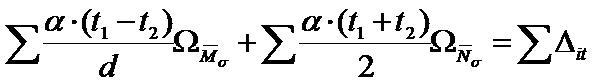
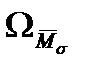и 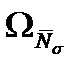- площади суммарных эпюр M и N.

Окончательную эпюру изгибающих моментов строят путем суммирования единичных эпюр на соответствующее значение неизвестных:

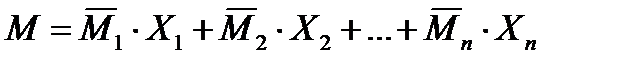(1).

3. Общий способ определения коэф-ов и свободных членов системы канонич. ур-ий метода перемещений.

Основная система метода перемещений получается путем введения дополнительных свя зей и появлению реактивных моментов во введенных заделках и реактивных сил в дополнительных стержнях. Эти дополн реак силы и моменты можно обратить в 0, если заделку повернуть на углы, равные действит углам поворота узлов рамы и сместить узлы рамы, так чтобы лин перемещ так же были равны действит смещ. После этого деформ основ сист и усилия в ней будут равны деформ и усилиям зад сист. Отрицание реак М и усилий во введен заделках и стержнях основ сист лежит в основе уравн метода перемещ. Уравнения метода перемещ – уравн равновесия.

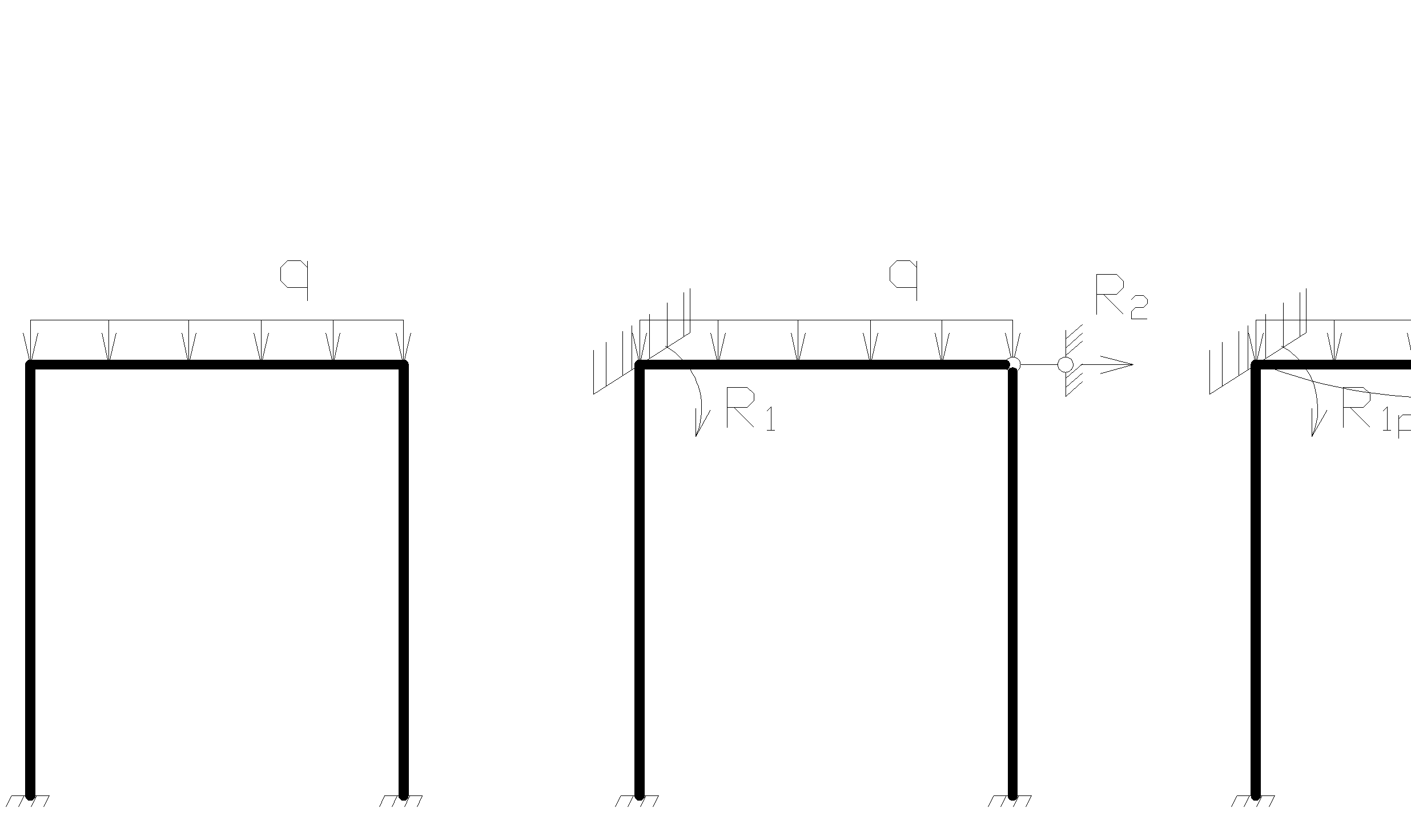
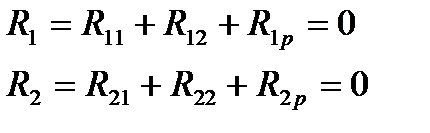
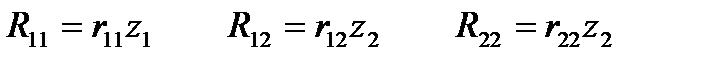
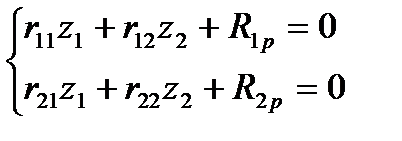
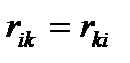
Определение коэф при неизвестных: 2 способа : 1) статический 2) общий (основанный на применении теорема о взаимности работ)1)Выбор основной системы метода перемещ.2) Построение эпюр изгиб моментов в основ системе метода перемещ от единичн смещений и от внеш нагрузки.

Поскольку коэф свобод членов канон ур-ний явл реакциями связей основ системы, то они опред из уравн-ий равновесия.Коэф представ реактив момент во введ заделках опредл из уравн равновес вырезанного узла. Коэф представл реактив усилия в дополн стержнях опред из условия равновес всех факторов действ на отсечен часть рамы

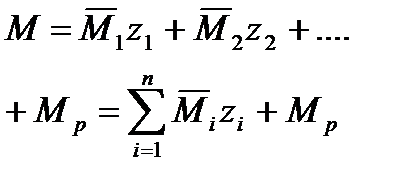
Общий способ применим к любой системе и позвол путем перемнож эпюрполучить формулы для реакций в общем виде.

5 Расчет рам смешанным способом.

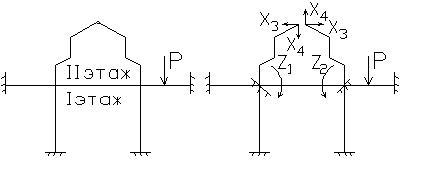
При смешанном методе расчета часть неизвестных представляет собой усилия – силы, моменты (как при расчете методом сил), а другая часть – перемещения – повороты, поступательные. Применение этого метода к рассматриваемой системе позволяет свести задачу к решению четырех уравнений с 4-мя неизв естными вместо 11 – по методу сил и 14 по методу перемещений. За неизвестные удобно принять углы поворота узлов первого этажа и усилия, возникающие в верхнем шарнире. Составим канонические уравнения смешанного метода, смысл к-ых заключается в том, что в основной системе реакции, возникающие во введенных связях по направлению неизвестных перемещений Z₁ и Z₂, а также перемещения по направлвению неизвестных усилий X₃ И Х₄ равны нулю:

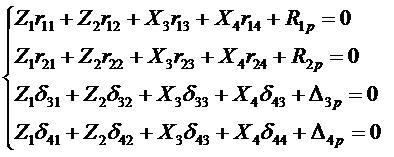
Сумма перечисленных реакций равна нулю, т.к. в действительности заделки нет, а следовательно нет и ее реакции. Таким образом, первое уравнение является уравнение статики, оно выражает мысль о равенстве нулю реактивного момента, возникающего в первой заделке от действия неизвестных и заданной нагрузки. Такую же мысль выражает и первое уравнение.

Сумма перечисленных перемещений равна нулю, т.к. в действительности верхний шарнир не разрезан, а поэтому точки приложения сил Х₃ расходиться не могут. Таким образом третье уравнение выражает мысль о равенстве нулю перемещения; его можно назвать уравнением кинематики.

6. Методы исследования устойчивости упругих систем

6. Метод исследования устойчивости упругих систем.

В задачах устойчивости используют энергетический и статический метод (есть еще динамический, но он редко применяется). Статический метод – заключается в составлении и интегрировании ДУ равновесия элемента упругой системы, находящейся в таком деформированном состоянии, к-ое отличается от исходного наличием перемещений, вызывающих новый вид деформации.

Энергетический метод – основан на использовании энергетических признаков устойчивого и неустойчивого равновесия упругой системы, согласно к-м система находится состоянии устойчивого равновесия, если ее потенциальная энергия минимальна по сравнению с энергией смежных равновесных. Если ε_р=max, то равновесие устойчиво.

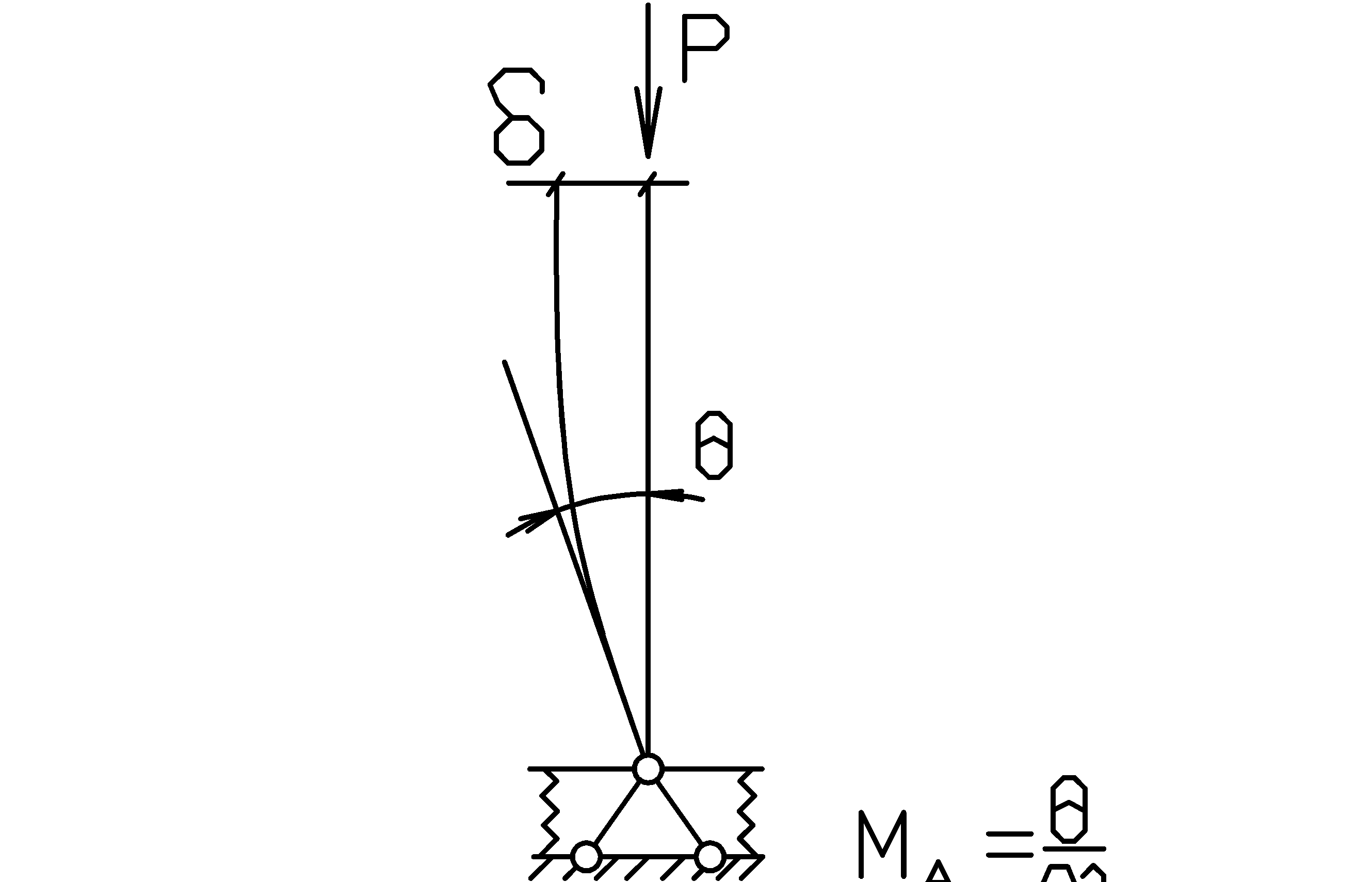
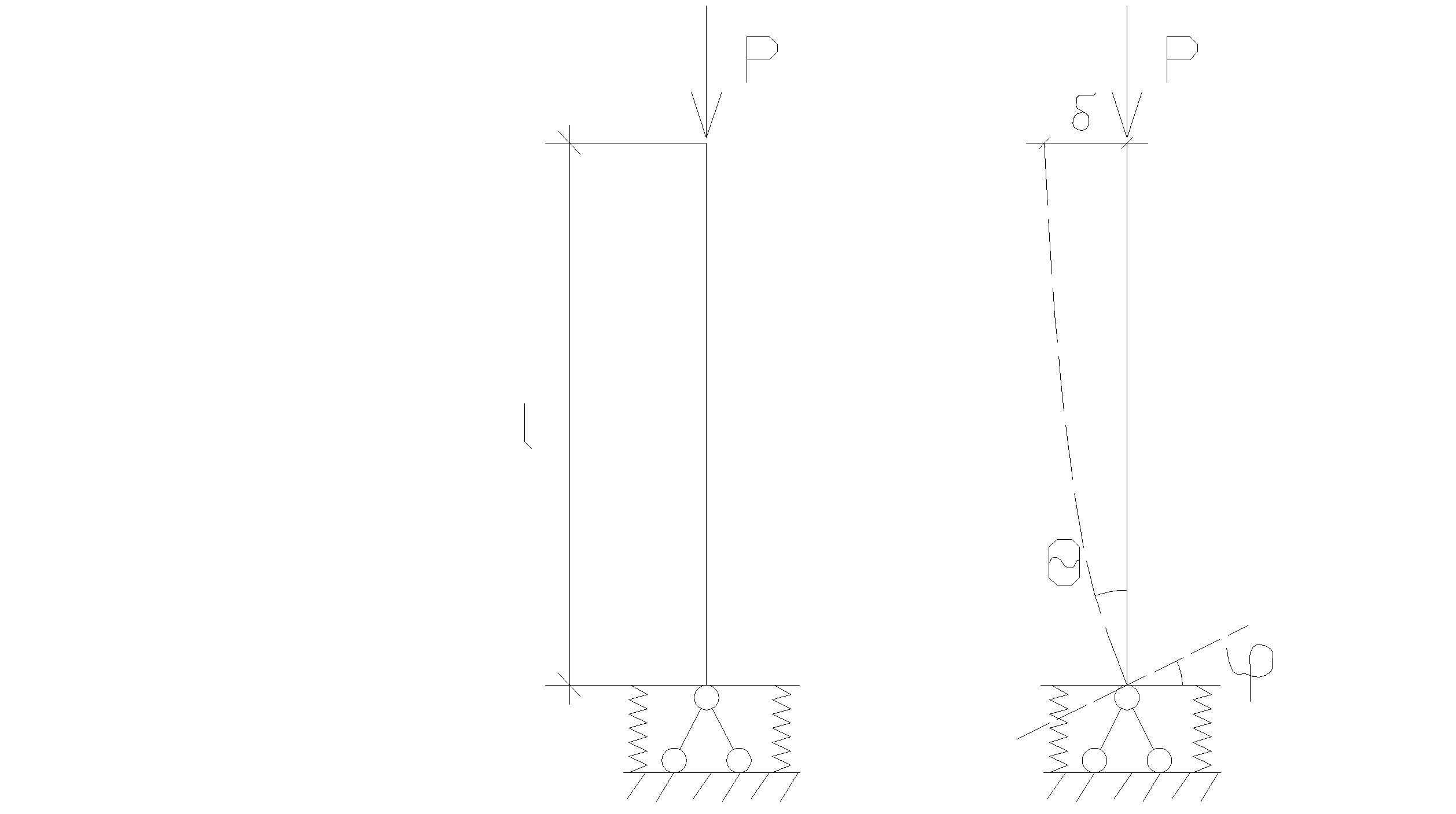
Пример: Определить Р_кр для жесткого стержня. М=1; φ=1 – угол поворота. Стат. метод: ΣМ_А=0 .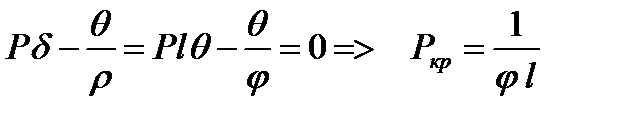

Энергетический метод: Выразим изменения упругой системы через работу силы Р. Работа силы Р=А=Pl(1-cosθ)=2Plsin² (θ/φ)=(Plθ²)/2. Работа совершаемая опорным моментом, определяется 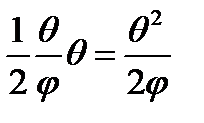. Изменение полной упругой энергии 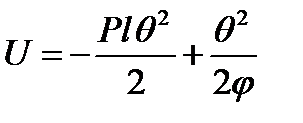. Энергетическим критерием потери устойчивости системы явл. условие: .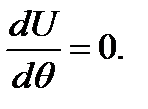

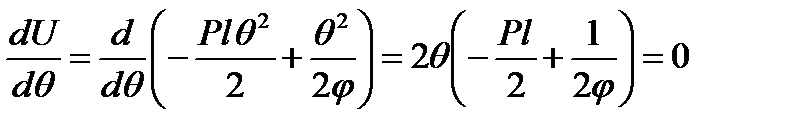
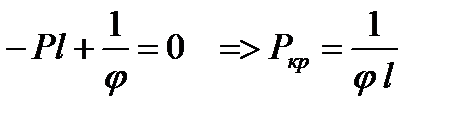4. Энергетический метод исследования устойчивости

4. Энергетический метод исследования устойчивости.

Основан на исследовании энергетических признаков устойчивого и не устойчивого равновесия упругой системы, согласно которым система находится в состоянии устойчивого равновесия, если её потенциальная энергия минимальна по сравнению с энергией смежных равновесных систем.

Если 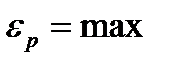, то равновесие устойчиво.

Пример: Определить Р_кр для жёсткого стержня.

Выразим изменения упругой энергии системы через работу силы Р. Работа силы:

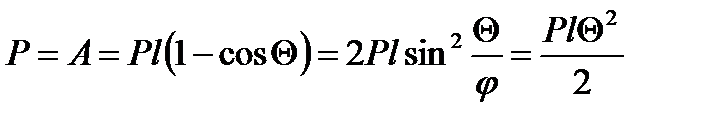
Работа совершаемая опорным моментом, определяется:

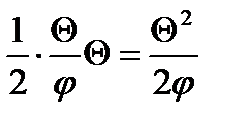
Изменение полной упругой энергии:

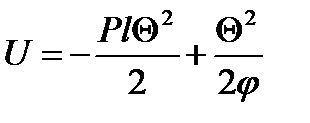Энергетическим критерием потери устойчивости системы является условие:

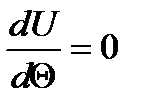
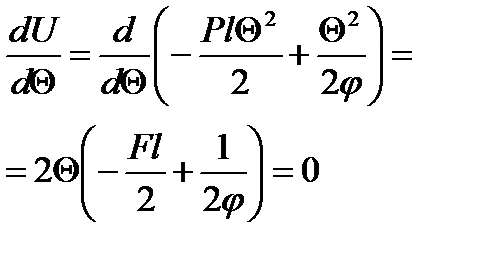
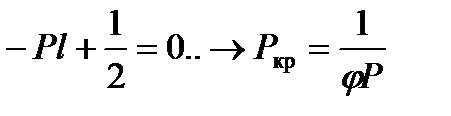
2 Значение устойчивости сжатых стержней в изогнутости балок и других элементов в решении надежности сооружений.При проектировании инженерных сооружений часто бывает недостаточно обычных методов расчета на прочность. Чтобы получить полное представление о надежности сооружения в особенности это относится к таким сооружениям, которые состоят из гибких сжатых и сжато – изогнутых элементов. Как правило для таких сооружений решающим фактором, определяющим несущую способность таких элементов является возможность потери устойчивости сооружения в целом его элементов. Понятие о потери устойчивости всегда связано с деформацией, но обычно потеря устойчивости происходит в результате нарушения равновесия между внешними и внутренними силами, поэтому нарушение равновесия может быть устойчивым и неустойчивым границы между этими двумя состояниями равновесия называется безразличным состоянием системы. Простейший пример потери устойчивости прямолинейной формы центрально - сжатым прямым стержнем.Потеря устойчивости может быть не только при сжатии, но и при растяжении. Потеря устойчивости плоской формы изгиба балок прямоугольного и двутаврового сечения проявляются изгибанием в горизонтальной плоскости и кручением балки.Форма равновесия называется безразличной если при условии 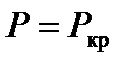элемент работающий на сжатие не выходит из первоначального состояния равновесия, а при возникающей внешней изгибающей поперечной силы элемент переходит в некоторое изогнутое состояние и далее при ее исчезновении элемент не принимает первоначальную форму – остается в изогнутом состоянии.

Форма равновесия называется неустойчивой при условии 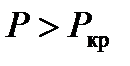элемент работающий на сжатие выходит из первоначального состояния равновесия, элемент переходит в некоторое изогнутое состояние. При достижении сжимающей силы 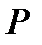критического значения возможны три формы равновесия: прямолинейная (оказывается неустойчивой), криволинейная (вызванная искривлением стержня) и ситуация когда для шарнирно опертого стержня возникает ряд полуволн искривленной формы.

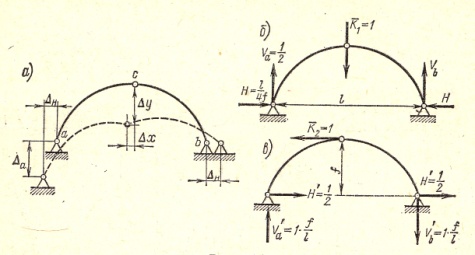
7. Определение перемещений в стат-ки опред. сист-ах от осадки опор.

Перемещения от случайных осадок опор. Осадки опор могут быть случайными вызванными просадкой грунта, размывом, оползнем и др. причинами). При отсутствии нагрузки на сооружение осадки могут возникнуть под действием нагрузки в рез-те податливости основания. Рассматривая первый случай будем считать, что 3-х шарнирная арка получает одинаковые горизонтальные смещения опор ΔH и верт. смещение левой опоры Δа , причем величины смещений зданий от действующих осадок опор в стат. опред. системах внутр. усилия не возникают. Часто необходимо определить новое положение системы. Пусть нужно найти вертик. и гориз. перемещения ключевого шарнира с. Для определения верт. перемещения по ф-ле Мора представим един. сост. действ. вертик. силы 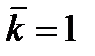. Составим сумму работ:

1∙Δy-V_aΔa-HΔ_H-HΔ_H=0 Δy= V_aΔa+2HΔa.

Для определения Δx:

1∙Δx-V΄_aΔa-H΄Δ_H-H΄Δ_H=0 Δx= V΄_aΔa.