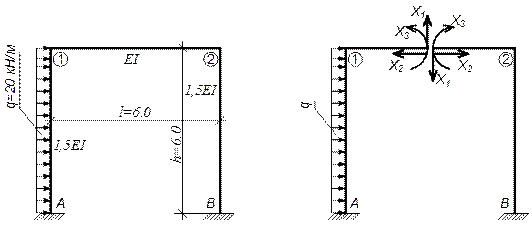
Пример 3. Построить эпюры Q , М и N для рамы. Жесткости элементов указаны на рисунке.
1. Рама трижды статически неопределима, так как
Л = 3К -Ш = 3 ∙ 1—0 = 3 (или Л = С0П - 3 = 6 - 3 = 3).
2. Для упрощения расчета используем симметрию заданной системы.
3. Составим канонические уравнения, которые в порядке написания будут выражать условия равенства нулю: вертикального взаимного сдвига смежных сечений в месте разреза, взаимного горизонтального смещения этих сечений и их взаимного угла поворота:
КАНОНИЧЕСКИЕ УРАВНЕНИЯ
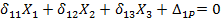
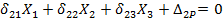
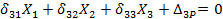
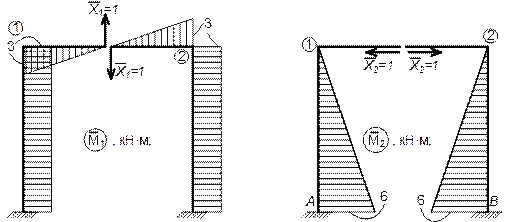
4. Далее построим эпюры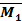 
, 
, 
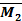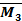и 
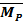от поочередного раздельного нагружения основной системы силами 
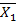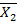= 1, 
= 1,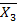 
= 1 и заданной нагрузкой.
Сопоставляя построенные эпюры, приходим к заключению, что эпюры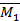 
и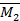 
, а также эпюры 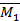и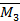 
взаимно ортогональны по свойству прямой и обратной симметрии. Следовательно,
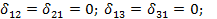
Теперь канонические уравнения можно представить в более упрощенном виде:
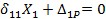
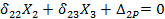
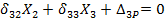
Как видим, система трех уравнений с тремя неизвестными распалась на две независимые, системы: одно уравнение с одним неизвестным Х1 и два уравнения с двумя неизвестными Х2 и Х3.
Следует иметь в виду, что выбор основной системы путем разреза симметрич- ной заданной системы по оси симметрии и введения в месте разреза симметричных и обратно симметричных лишних неизвестных всегда позволяет привести общую систему канонических уравнений к двум независимым системам, одна из которых содержит только симметричные, другая — только обратно симметричные лишние неизвестные.
Вычислим входящие в полученные уравнения перемещения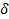 
и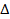 
:
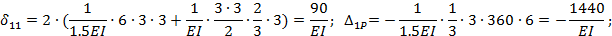
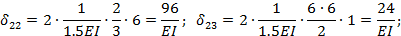
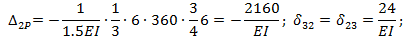
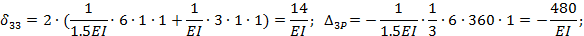
Обращаем внимание, что при определении перемещений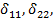 
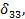
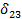сразу же после первого знака равенства поставлен коэффициент 2. Это значит, что перемножение соответствующих эпюр ведется для левой (или правой) части основной системы и результат удваивается.
5. Подставив найденные значения перемещений в канонические уравнения, получим:
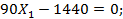
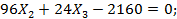
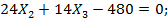
Из первого уравнения находим Х1= 1440/90 = 16 кН, а из совместного решения второго и третьего уравнений получим: Х2 = 24,37 кН; Х3 = —7,48 кН∙м.
Отрицательное значение моментов Х3 свидетельствует о том, что их направления первоначально были выбраны неправильно.
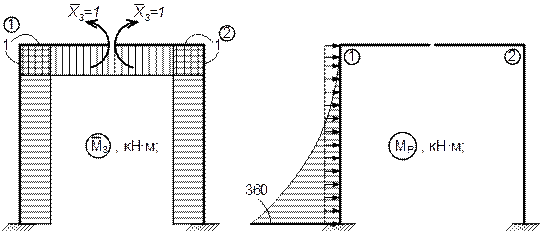
6. Теперь значения всех сил, приложенных к основной системе известны, следовательно, можно приступить к построению окончательных эпюр М, Q и N. Не приводя вычислений, которые могут быть выполнены, как и в ранее решенных примерах, изображаем окончательные эпюры.
Пример расчета статически неопределимой рамы с использованием метода сил
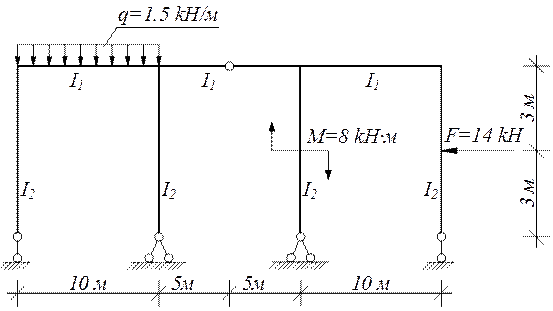
I 1 / I 2 =2; I 1 =2∙ I 2 ;
 |
I 2 = I ; I 1 =2∙ I
Определяем число лишних связей:
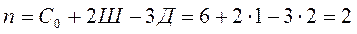
где С0 - число опорных стержней;
Ш – приведенное число простых шарниров, связывающие диски между
собой;
Д – число дисков.