Запуск авиационных двигателей

Дата: 2025-04-30; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

13.1. Условия работы двигателя при запуске

Запуск газотурбинных авиадвигателей (ГТД) выполняется автомати­чески, в соответствии с программой запуска. В состав системы запуска входят стартер (электрический, воздушный или газотурбинный), системы электрическая (или электронная) управления запуском, зажигания, пусковая и рабочая топливные, устройства контроля параметров двигателя при запуске, защиты двигателя и агрегатов системы запуска от опасных ре­жимов, а также блокировочные устройства, защищающие от неправиль­ных действий при запуске. Для запуска ротор авиадвигателя (у двухконтурного авиадвигателя ротор второго каскада компрессора и вместе с ним первая ступень турбины) разгоняются стартером до угловой скорости, при которой рабочее топливо горит устойчиво. В процессе разгона вклю­чается система зажигания, в камеры сгорания сначала к пусковым, а за­тем к рабочим форсункам подается топливо, вступает в работу турбина. В дальнейшем ротор разгоняют совместно стартер и турбина, которая в конце запуска должна развивать момент, достаточный для самостоя­тельного быстрого выхода двигателя на режим малого газа.

Режимом малого газа ГТД называют устойчивый режим работы с ми­нимальной мощностью, с которого обеспечивается надежный выход на любой рабочий режим за заданное время приемистости. Управление запуском состоит в дистанционной коммутации электрических управляю­щих цепей систем и агрегатов, обеспечивающих запуск в соответствии с программой. Управление выполняет система электроавтоматики по угловой скорости авиадвигателя и по времени.

Непосредственным показателем режима работы двигателя при запуске является его угловая скорость. В некоторых системах запуска ее исполь­зуют как основной параметр запуска, в соответствии с которым осуществляется вся программа запуска. Одновременно все этапы запуска контролируют по времени, чтобы запуск чрезмерно не затянулся. В дру­гих системах запуска двигатель запускают по временной программе (дви­гатели АИ-20, -24, -25, все двигатели серии Д-ЗО). В таких системах обязательно вводят контроль окончания запуска и защиту от опасных режимов по угловой скорости.

Система запуска запускает авиадвигатель на земле, выполняет холод­ную прокрутку и ложный запуск, запуск в воздухе и аварийное прекра­щение запуска. Основным и наиболее полным (по совокупности и режи­мам работы агрегатов, участвующих в запуске) видом запуска авиадви­гателя является его запуск на земле. Он включает все операции и весь комплекс систем, работающих при запуске.

Запуск авиадвигателя на земле разделяют на этапы:

первый - разгон ротора ГТД до угловой скорости ω₁ при которой производительность компрессора достаточна для надежного воспламене­ния топлива и вступления в работу турбины;

второй - сопровождения стартером ротора ГТД до угловой скорости ω₂, при которой турбина развивает мощность, достаточную для дальней­шего самостоятельного разгона двигателя с заданным ускорением; при ω= ω₂ стартер отключается;

третий - самостоятельный выход авиадвигателя на режим малого газа (разгон от ω₂ до ω_МГ).

Зависимость моментов, действующих на вал авиадвигателя (или на вал стартера, если все моменты приведены к валу стартера), представлены на рис. 13.1.

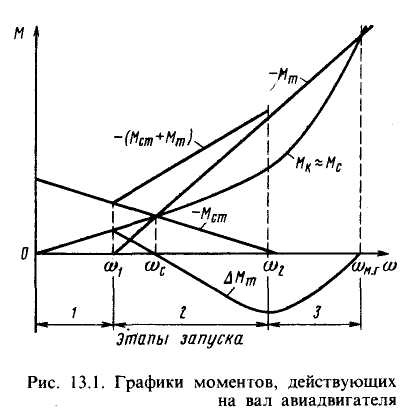
Момент сопротивления условно считают положительным и рассчитывают по формуле:

М_С=М_ТР+М_К,

где М_ТР - момент трения; М_К - момент компрессора.

Поскольку М_ТР<< М_К принимают, что М_С≈ М_К=К_К·ω², где К_К - коэффициент компрессора. Моменты стар­тера М_СТ и турбины М_Т дви­жущие. Они действуют про­тив моментов сопротивления, но на рис. 13.1 они отложены в той же четверти, что и момент сопротивления (взя­ты с обратным знаком). Мо­мент турбины М_Т=К_Т·ω (здесь К_Т - коэффициент пропорциональности).

Уравнения движения си­стемы статер-ротор авиа­двигателя для первого, вто­рого и третьего этапов запуска имеют вид:

1) М_СТ - М_К = М_СТ - К_К·ω² = J(dω/dt);

2) М_СТ +М_Т -М_К = М_СТ + К_Т·ω - К_К·ω² = J(dω/dt);

3) М_Т - М_К = К_Т·ω - К_К·ω² = J(dω/dt),

где М_Т - М_К = ∆ М_Т; J — суммарный момент инерции всех вращающихся частей, приведенный к валу якоря стартера (J = J_АД + J_CT. Здесь J_АД - момент инерции роторов и воздушного винта авиадвигателя, J_CT - момент инерции стартера).

При анализе процесса запуска все моменты сопротивления, движущие моменты и моменты инерции вращающихся тел, входящие в уравнение движения системы, должны быть приведены к валу стартера.

Характерными угловыми скоростями вращения ротора ГТД при запуске являются: ω₁ -начала подачи топлива в камеру сгорания; ω_С - соответ­ствующая условию М_Т = М_К; ω₂ - при отключении стартера; ω_М - макси­мальной мощности стартера; ω_К - режима холодной прокрутки, ω_МАХ - максимальная ротора ГТД. Для сокращения записей вводят "понятие относительной угловой скорости 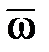= ω/ω_МАХ.

Наиболее ответственным является второй этап запуска. Он характерен самыми высокими температурами турбины и узким диапазоном устой­чивой работы компрессора. Увеличение продолжительности запуска при­водит к повышению температуры лопаток турбины, снижению их проч­ности и ресурса.

В системах запуска ГТД применяют главным образом электрические и воздушные стартеры. На современных двухконтурных ТРДД используют воздушный стартер, представляющий собой одноступенчатую воздушную турбину с понижающим редуктором и=ω_Т/ω_{ВЫХ.ВАЛА} = 8-10 и обгонной муфтой для расцепления выходного вала стартера и трансмиссии авиа­двигателя. В состав стартера также входят сигнализатор давления воз­духа перед силовым аппаратом турбины, узел управления стартером, содержащий электромагнит и центробежный выключатель, который за­щищает стартер от опасных угловых скоростей.

Воздух, необходимый для работы стартера, берется либо от ВСУ самолета (турбоагрегата ТА-6, -8), либо от наземной УВЗ (турбоагрегата, установленного на автомашине), либо от компрессора работающего авиа­двигателя. На самолетах Ил-62 с авиадвигателями НК-8-4 для запуска авиадвигателя используют воздушную турбину ППО-62М привода по­стоянных оборотов синхронного генератора.

Управляющим устройством системы электроавтоматики запуска явля­ется автомат запуска пусковой панели АПД. Она подает команды на коммутацию электрических цепей управления агрегатами запуска в соот­ветствии с заложенной в ней программой по времени и по угловой скорости. Топливная система (насос-регулятор, насосы подкачки топлива, автомат дозировки и другие ее элементы) непосредственно к системе запуска не относится, но обеспечивает запуск. Управляет электромагнит­ными клапанами пускового и рабочего топлива также автомат запуска пусковой панели АПД.

Характерные угловые скорости ротора в о. е. для газотурбинных авиа­двигателей представлены в табл. 13.1.

Таблица 13.1

Характерные относительные значения угловых скоростей роторов авиадвигателей

Угловая скорость	ТРД	ТРДД	ТВД
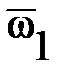
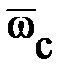
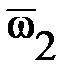
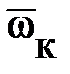
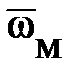
	0.09-0.12 0.10-0.16 0.30-0.40 0.13-0.25 0.13-0.15	0.15-0.20 0.23-0.28 0.40-0.45 0.23-0.25 0.23-0.27	0.14-0.18 0.30-0.35 0.45-0.55 0.20-0.25 0.20-0.25

При запуске ГТД стремятся достичь минимального времени второго этапа запуска. На этом этапе одновременно работают стартер и турбина двигателя, задача заключается в управлении стартером таким образом, чтобы он обеспечивал надежное сопровождение двигателя и достижение им угловой скорости ω₂ за заданное время t₂ (время разгона до угловой скорости ω₁ ничем не регламентировано, кроме необходимости сокраще­ния общего расхода энергии на выполнение запуска).

При использовании воздушных стартеров управление ими сводится к поддержанию постоянства давления воздуха перед сопловым аппаратом. Если для запуска авиадвигателя применяют электрические стартеры, уп­равление заключается в изменении напряжения питания и потока возбуж­дения стартера по нужному закону при разгоне ротора газотурбинного двигателя.

13.2. Управление электростартерами при запуске ГТД

От электростартеров запускают авиадвигатели АИ-20К,-24 на самоле­тах Ан-12, -24; газотурбинные двигатели ВСУ (ТГ-16, ТА-6, -8) и авиа­двигатели на вертолетах. В качестве стартеров используют стартер-гене­раторы (СТГ) постоянного тока. Необходимость сокращения времени запуска, расхода электроэнергии и уменьшения потерь в цепях стартеров привела к разработке способов управления электростартерами. Их сущ­ность заключается в изменении напряжения на якоре и потока возбуж­дения стартера для улучшения временных и энергетических показателей запуска.

Все эти способы подчинены общей цели: сделать запуск наилучшим по определенным показателям.

Для улучшения характеристик пуска определяют оптимальное переда­точное отношение стартер-авиадвигатель для минимизации времени разгона стартера от какой-то исходной до заданной конечной угловой скорости. Для этого рассматривают выбор передаточного отношения для разгона привода от начала запуска до угловой скорости ω₁ при которой вступает в работу турбина. При заданном максимальном (пусковом) мо­менте стартера М_СТ.К = М_СТ.МАХ минимизация этого интервала времени позволяет уменьшить потери, общий расход энергии и время запуска. Для упрощения задачи считают, что основным нагрузочным моментом является динамический момент М_ДИН =J(dω/dt), а моментом компрессора М_К, приведенным к валу стартера, пренебрегают.

Так как СТГ имеет параллельное возбуждение, уравнение его меха­нической характеристики имеет вид:

М_СТ = М_СТ.К(1 - ω/ω₀).

Уравнение движения системы стартер-ротор ГТД записывают так:

J(dω/dt) = М_СТ.К(1 - ω/ω₀),

откуда

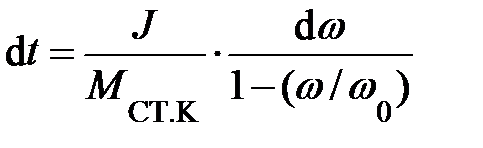или .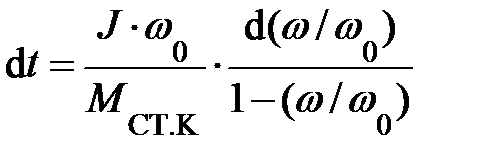

В результате интегрирования время разгона от ω = 0 до ω₀ = ω₁ опре­деляется уравнением

t₁=(J ω₀/М_СТ.К)ln[1/(1- ω₁/ω₀)].

Передаточное отношение и между стартером и авиадвигателем нахо­дят из выражения ω_СТ= uω_АД, откуда и = ω_СТ / ω_АД.

Приведенный к валу стартера момент инерции J = J_CT + (1/ и ²) J_АД. Учитывая, что при использовании для запуска стартер-генераторов пере­даточное отношение и = 1.35 – 1.42, приведенный к якорю стартера мо­мент инерции авиадвигателя (1/ и ²) J_АД>> J_CT. Без ущерба для точности принимают, что J_CT≈(1/ и ²) J_АД.

Время разгона до угловой скорости ω₁ с учетом допущений

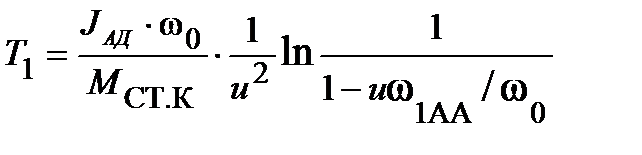(13.1)

Для определения передаточного отношения 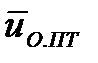, обеспечивающего минимум времени разгона до угловой скорости ω₁ уравнение (13.1) ис­следуем на экстремум:

,

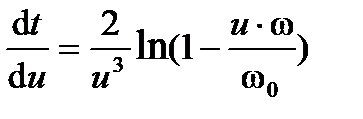откуда - ;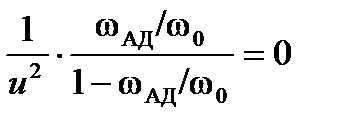

ln(1-uω_1АД/ ω₀)=0.5 uω_1АД/ ω₀(1-uω_1АД/ ω₀).

В результате графического решения этого уравнения получают опти­мальное передаточное отношение, обеспечивающее минимум времени раз­гона системы стартер - авиадвигатель до угловой скорости, при которой вступает в работу турбина. Как правило, это отношение

u_ОПТ=0.73·ω₀/ω_1АД.

В электрических системах запуска ротор авиадвигателя разгоняют СТГ, который в полете работает в генераторном режиме, а при запуске - в стартерном. При работе в режиме стартера стартер-генератор должен развивать необходимую механическую мощность для того, чтобы быстро разогнать ротор авиадвигателя. Максимальную мощность СТГ должен развить при угловой скорости ω₁ когда момент сопротивления макси­мален (см. рис. 13.1):

Р_СТ = ω₁ (М_СТ + М_ДИН) = М_Э.СТ ·ω₁,

где М_ДИН - динамический момент, необходимый для создания нужного ускорения dω/dt; М_Э.СТ - электромагнитный момент стартера.

Электромагнитный момент стартера М = С· I_aФ_МАХ; поток возбуждения в стартерном режиме имеет наибольшее значение. Электромагнитная мощность стартера Р_Э.СТ=М_Э.СТ ·ω₁= 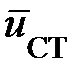·ω_1АД ·М_Э.СТ .

После того как запуск произошел, СТГ переходит в генераторный режим, работая с минимальной для этого режима угловой скоростью и тем же максимальным потоком Ф_МАХ. В данном случае электромагнит­ные моменты СТГ в стартерном и генераторном режимах равны М_Э.Г = М_Э.СТ; минимальной угловой скоростью для генераторного режима яв­ляется скорость малого газа авиадвигателя ω_МГД.

Электромагнитную мощность генератора Р_Э.Г=М_Э.Г ·ω_Г..МIN= М_Э.Г ·ω_МГД·u_Г, где ω_МГД угловая скорость малого газа двигателя u_Г = ω_Г / ω_АД.

При работе с минимальной угловой скоростью, номинальным током и максимальным потоком возбуждения СТГ развивает наибольший для генераторного режима момент. Соотношение электромагнитных мощ­ностей в стартерном и генераторном режимах находят, считая, что макси­мальные электромагнитные моменты машины в стартерном и генератор­ном режимах равны М_СТ.МАХ=М_Г.МАХ. Используя это условие и выражения для электромагнитных мощностей в стартерном и генераторном режимах, мощность стартера через мощность генератора и параметры обоих ре­жимов находят так:

Р_Э.СТ=Р_Э.Г · u_СТ ·ω_1Д К_П/ u_Г ·ω_МГД . (13.2)

Для оценки возможности использования СТГ для запуска ГТД опре­деляют мощность, которую он может развить, работая в стартерном режиме. С учетом кратковременности стартерного режима (60 - 70 с) ток I_СТ якоря стартера при запуске может превышать ток генераторного режима в К_П раз (I_СТ = К_П ·I_Г , где К_П - коэффициент перегрузки, равный 1.3 – 1.4). Для ГТД, запускаемых от стартер-генераторов, передаточные отношения равны:

u_СТ=ω_СТ/ω_АД=1.3-1.4; u_Г = ω_Г / ω_АД.≈0.5; 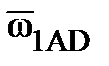≈0.1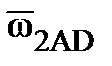5; ≈0.5

Подставив эти данные в формулу (13.2), оценивают соотношение мощ­ностей СТГ в стартерном и генераторном режимах. Если учесть, что в современных системах запуска напряжение V_CT на якоре СТГ составляет (2 - 2,2)U_Г.ПОТ, то Р_Э.СТ=Р_Э.Г (1.5 – 1.7) Р_Э.Г.

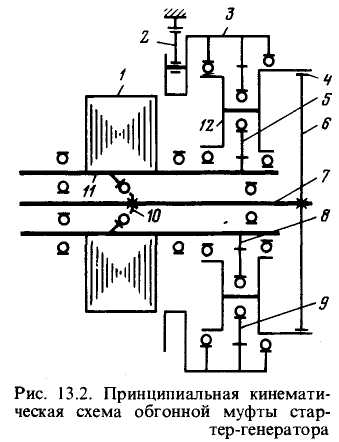
В стартер-генераторах, применяемых при запуске ГТТ, для повышения момента используют планетарный редуктор с обгонной муфтой. При работе в стартерном режиме угловая скорость выходного вала стартера, сцепленного с коробкой передач авиадвигателя, примерно в 3 раза меньше скорости вращения якоря СТГ. При работе СТГ в генераторном ре­жиме вращение от коробки передач авиадвигателя передается на якорь помимо редуктора. Изменение пе­редаточного отношения осуществ­ляют за счет обгонной муфты. Она при передаче движения от авиа­двигателя к генератору сцепляет ведущий (гибкий) вал с полым валом, на котором посажен пакет якоря. При передаче движения от СТГ к авиадвигателю сцепления полого и гибкого валов не происходит. Передача движения от полого вала к выходному валу осуществляется через планетарный редуктор (рис. 13.2).

При работе в стартерном режиме момент от якоря 1 через шестерню 8 и сателлиты 5 передается на корпус редуктора 3, который в этом режиме заклинивается храповой собачкой 2 и неподвижен. Сателлиты приводят в движение водило 12. Оно своей шестерней с внутренним зацеплением 4 через шестерню 6 вращает выходной вал, жестко связанный с гибким валом 7. В стартерном режиме муфта свободного хода не заклинена и полый вал связан с гибким через редуктор, уменьшающий угловую скорость гибкого вала в отношении 3.18:1. В генераторном режиме вследствие изменения направления передачи момента (от двигателя к ге­нератору) собачка 2 расцепляет корпус 3 редуктора и корпус стартера, а муфта свободного хода 10 заклинивает, сцепляя гибкий 7 и полый 11 валы помимо редуктора.

Угловая скорость обоих валов одинакова.

13.3. Способы управления электростартерами при запуске ГТД.

Прямой пуск

Запуск ГТД выполняют от СТГ, установленных на главных двига­телях, запуск ГТД вспомогательных силовых установок - от генераторов постоянного тока, входящих в состав ВСУ и работающих при запуске в стартерном режиме от самолетных аккумуляторов или наземных источ­ников. Необходимость уменьшения времени запуска, потерь и расхода электроэнергии при запуске привела к разработке ряда способов управ­ления электростартерами воздействием на подводимое к ним напряжение и на поток возбуждения. Критериями качества работы стартера при запуске являются: к. п. д. пуска η=А_К/ А_Э - отношение запаса кинетической энергии системы к потребленной стартером при запуске электроэнергии; время пуска t_П; равномерность потребления тока (важная характеристика для учета расходования энергии аккумуляторов). ГТД запускают от аэродромных источников и от самолетных ВСУ. От аккумуляторов за­пускают газотурбинные двигатели вспомогательной силовой установки.

Для упрощения оценки качества запуска ГТД при использовании раз­личных способов управления стартерами вводят следующие допущения:

основной нагрузкой стартера является динамический момент, так как запуск - это переходный процесс привода стартер-авиадвигатель, обла­дающего большим моментом инерции и протекающий со значительными ускорениями. По этой причине для простоты анализа пренебрегают мо­ментами компрессора и турбины, считая, что неучет их действия не сказывается существенно на процессе разгона ротора. В реальных системах запуска при ложном запуске, когда не работает турбина, за время цикла угловая скорость отключения турбины не достигается. Система при этом режиме работы отключается по времени. Обычно в процессе запуска момент турбины разгружает стартер и ускоряет разгон, так как обычно система отключается по угловой скорости раньше отработки цикла за­пуска. Однако учет влияния моментов М_К и М_Т усложняет анализ работы стартера, поэтому ими пренебрегают;

пренебрегают электромагнитными переходными процессами;

не учитывают механические и магнитные потери в стартере и влияние реакции якоря на его механические характеристики.

При запуске ГТД применяют следующие способы управления стар­терами: прямой пуск - включение стартера на постоянное напряжение; ступенчатое уменьшение потока возбуждения стартера; плавное уменьше­ние потока возбуждения стартера; многоступенчатое повышение напряже­ния на якоре стартера; плавное повышение напряжения на якоре стартера.

В реальных системах запуска авиадвигателей и газотурбинного дви­жения ВСУ эти способы применяют комплексно, что позволяет получить достаточно высокие показатели качества запуска. Угловая скорость отклю­чения стартера ω₂ составляет около 70 % от его скорости идеального XX при номинальном потоке возбуждения Ф_НОМ.

Прямой пуск состоит в разгоне системы стартер - ГТД при включении стартера на номинальное напряжение. У стартера с параллельным, воз­буждением обмотка возбуждения подключается несколько раньше обмотки якоря. Пуск происходит при постоянном потоке Ф= Ф_НОМ =const. Урав­нение движения привода при М_С = 0 имеет вид:

М = J (d ω /dt),

Где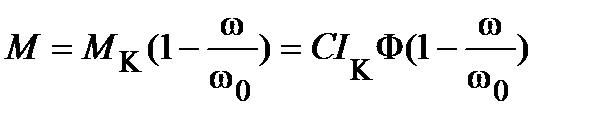

После преобразования получают:

.

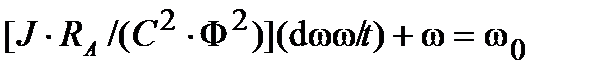Так как JR_A/(C²Ф²)=Т_М, то Т_М (dω /dt) +ω= ω₀.

Отсюда ω = ω₀+(ω_НАЧ- ω₀)exp(-t/Т_М)

При ω_НАЧ =0; ω = ω₀ [1-exp(-t/Т_М)];

ω = ω₂ = 0.7ω₀,

.

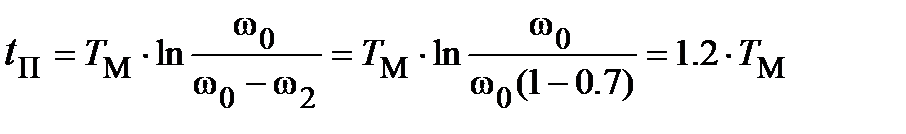Потребленная стартером из сети при пуске электроэнергии

.

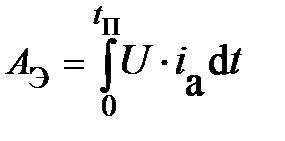Используя соотношения U=С·ω₀·Ф и М=С·I _а·Ф = J·(dω/dt), найдем, что I _а = [J/С·Ф)]·(dω/dt).

Поставив значения U и I _а в выражение для расхода электроэнергии, получают:

.

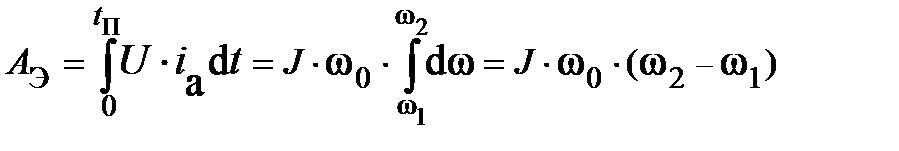При ω₁=0 и ω₂ = 0,7 имеем 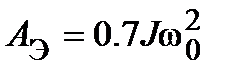. Тогда

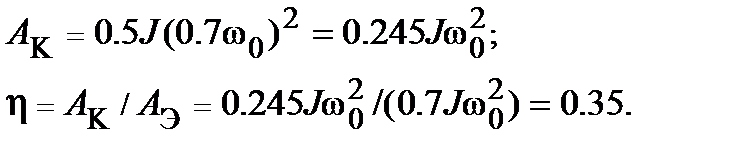
При t = 1,2T_M в конце запуска значение тока i_a=I_П·ехр(-t / T_M)= I_П, а отношение пускового тока к току отключения равно 3,33.

Как видно, процесс запуска заканчивается сравнительно быстро, к. п. д. невысок, неравномерность тока значительная. В чистом виде из-за малого к. п. д. и трудности достижения ротором авиадвигателя (и соответственно стартером) угловой скорости отключения ω_К, этот способ пуска исполь­зуют только для сравнения с более совершенными, которые рассмотрены в разделах 13.4-13.6.

13.4. Ступенчатое уменьшение потока возбуждения

Ступенчатое уменьшение потока возбуждения стартера применяют для управления им в системах запуска турбоагрегата ТГ-16. Напряжение на якоре стартера в течение всего запуска постоянно и равно номинальному. На первом этапе пуска стартер работает при максимальном магнитном потоке Ф₁ значительно большем, чем поток Ф₂ на втором этапе (рис. 13.3).

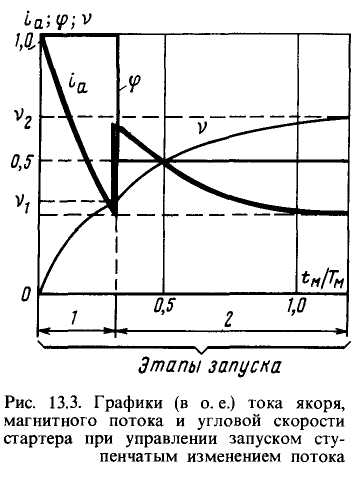
Поток от значения Ф₁ до значения Ф₂ уменьшается при угловой скорости стартера ω₁, которая должна быть достаточно близка к угловой скорости идеального XX ω₁₀ = U /(СФ₁). В противном случае уменьшение потока приведет к провалу, а не к возрастанию угловой скорости. В реальных системах запуска поток стартера уменьшают после вступления в работу турбины и частичной загрузки стартера. Стартер на втором этапе обеспечивает надежное сопровожде­ние турбины до скорости его отключения ω₂ и сокращает время второго этапа.

Электроэнергия, потреблен­ная от источника за весь за­пуск,

.

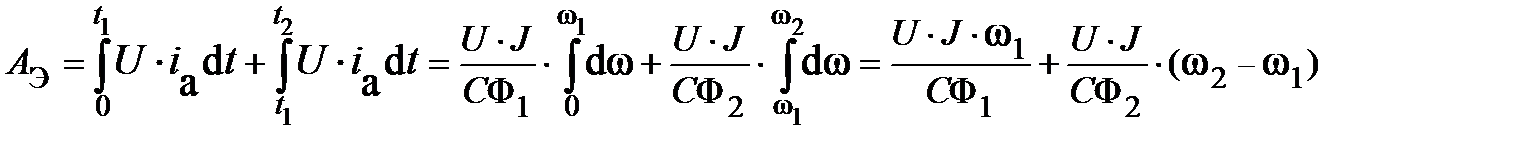В качестве условия переключения принимают равенство тока якоря в момент переключения и в конце пуска I₁ = I₂ или (U - C ω₁ Ф₁)/R_A=(U - C ω₂ Ф₂)/R_A, откуда ω₁ Ф₁= ω₂ Ф₂ .Выразив из последнего уравнения поток Ф₁, как Ф₁= Ф₂(ω₂/ω₁), получают

.

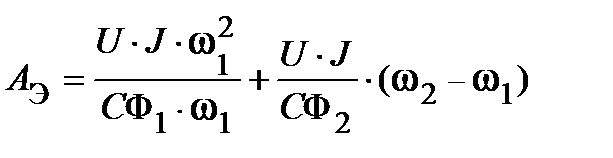Для определения оптимальной угловой скорости переключения потока находят экстремум функции

,

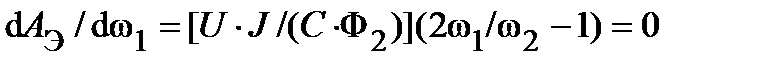откуда ω₁=ω₂/2. Считая, что U = С·ω₀·Ф₂; ω₂=0,7·ω₀ и, используя соот­ношение ω₁=ω₂/2, определяют:

расход электроэнергии при пуске:

;

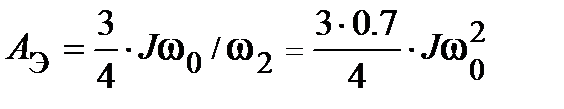к. п. д. пуска

.

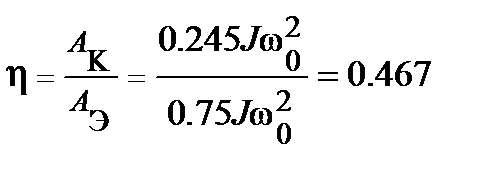Время пуска определяют как суммарное время работы на первом и втором его этапах: t_П= t₁ + t₂.

На первом этапе пуска для угловой скорости используют уравнение

ω₀=ω_С+(ω_НАЧ-ω_С)_·ехр(-t / T_M). Для этого этапа ω=ω₁= ω₂/2; ω_С= ω₀/2; ω_НАЧ=0.

Тогда 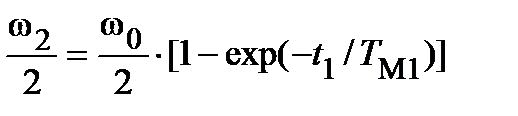, где ;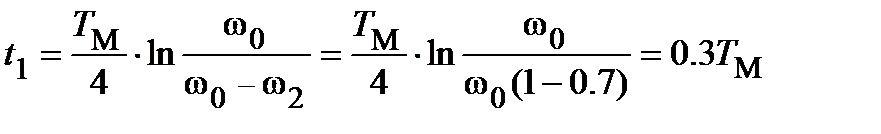

Здесь .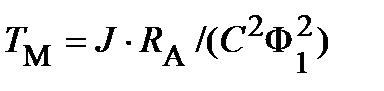

Электромеханическая постоянная времени на первом этапе:

.

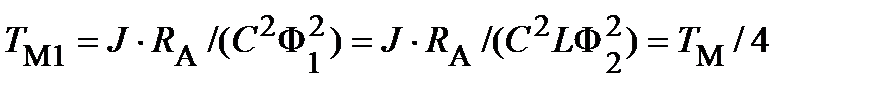Используя общее решение для второго этапа ω=ω_С+(ω_НАЧ-ω_С)_·ехр(-t₂/ T_M) и подставляя значения ω=ω₂=0.7ω₀; ω_НАЧ=0.5 ω₂=0.35 ω₀; ω_С=ω₀, получают 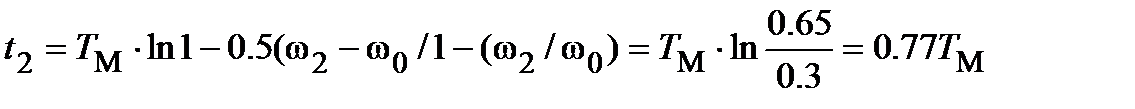. Время работы стартера t_П=1,07T_M.

Изменение тока при этом способе управления для аккумуляторной батареи благоприятнее, чем при прямом пуске. Основной бросок тока (пусковой ток) на первом этапе быстро затухает. Второй бросок тока значительно меньше первого. Ступенчатое уменьшение потока возбужде­ния имеет преимущества перед прямым пуском по энергетическим пока­зателям и по времени запуска. Авиагенераторы, применяемые при запуске ВСУ в качестве стартеров, допускают значительную кратность тока воз­буждения.

В системах запуска ВСУ поток меняется в два этапа. На втором этапе ток возбуждения стартера ограничен сопротивлением в цепи возбуждения, на первом же это сопротивление шунтировано контактами контактора, управляющего запуском ГТД.

13.5. Плавное уменьшение потока стартера

Способ управления стартером плавным уменьшением его потока ши­роко применяют при запуске авиадвигателей от СТГ. При этом способе поток на втором этапе запуска двигателя плавно уменьшают. При этом возрастает угловая скорость и обеспечивается надежное сопровождение авиадвигателя до конца запуска. Уменьшение потока, как и при его ступенчатом изменении, должно начинаться при угловой скорости ω_1, достаточно близкой ω₀₁= U/(CФ₁). Если поток начать снижать слишком рано, угловая скорость может упасть, а не возрасти. Поток возбуждения стартера, начиная с угловой скорости ω₁ уменьшают по такому закону, который при нарастании угловой скорости обеспечил бы постоянство противо-э.д.с. машины Е=СωФ=const. При соблюдении этого условия поток возбуждения должен изменяться обратно пропорционально угловой скорости привода Ф=Е/(Сω), а ток якоря в процессе регулирования изменением потока должен оставаться постоянным, т. е.

I_А=(U-СωФ)/ R_А= const.

Постоянство тока и противо-э.д.с. означает и постоянство электро­магнитной мощности Р_Э= Е I_А=const. Поскольку при I_А=const электри­ческие потери в якоре постоянны 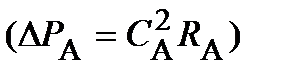, а магнитные потери вследствие уменьшения потока при увеличении угловой скорости меняются незначительно, считают, что такой закон изменения потока обеспечивает и приблизительное постоянство потребляемой мощности:

,

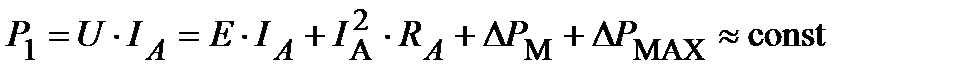где 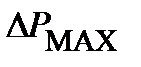- механические потери.

При работе с постоянным потоком максимальная электромагнитная мощность стартера достигается при t₁=0,69Т_М, что соответствует угловой скорости ω≈0,5ω₀. Диаграммы тока якоря, потока возбуждения и угловой скорости стартера (в о.е.) приведены на рис. 13.4,а.

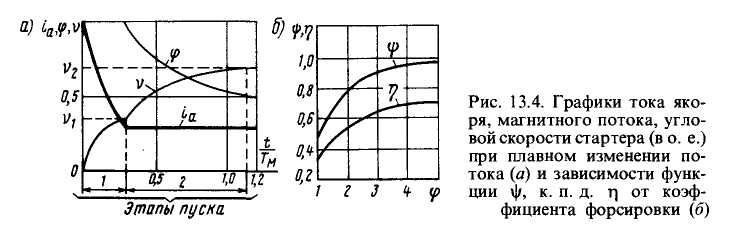
При постоянном напряжении питания якоря и максимальном потоке возбуждения стартера Ф₁=const система стартер - ротор ГТД разгоняется до угловой скорости ω₁. Начиная с момента времени t₁, соответствующего угловой скорости ω₁ поток возбуждения уменьшают таким образом, чтобы выполнялись усло­вия Е = СωФ=const и 1_А=const.

Поток на втором этапе запуска снижают от его форсированного зна­чения Ф₁ до номинального значения, соответствующего угловой скорости ω₂ в момент отключения стартера. Из условия постоянства противо-э.д.с. и тока якоря при работе на втором этапе запуска следует, что поток в функции от угловой скорости меняется по закону Ф(ω)=Ф_Н(ω₂/ω), где ω₂ - конечная угловая скорость стартера; ω - текущее значение угловой скорости. Максимальное значение потока равно Ф₁(ω)=Ф_Н(ω₂/ ω₂).

Электроэнергия, потребляемая стартером при запуске, равна суммарной энергии, которую стартер потребляет на первом и втором этапах запуска:

.

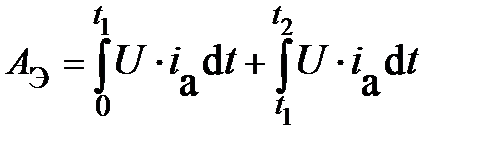Используя уравнение движения привода М-M_С= J(dω/dt), выражая ток в виде

i_a =[J/(СФ)](dω/dt), и учитывая, что U=Сω₀Ф_ПОТ, выражение для электроэнергии, израсходованной при запуске, записывают так:

.

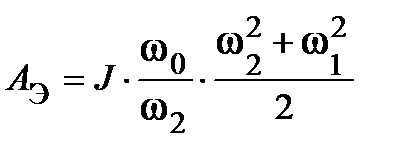Функция А_Э = f (ω₀) экстремума не имеет.

Запасенная системой в процессе разгона кинетическая энергия

.

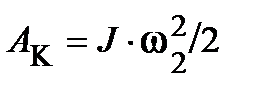К. п. д. запуска при этом способе управления определяют из соотношения:

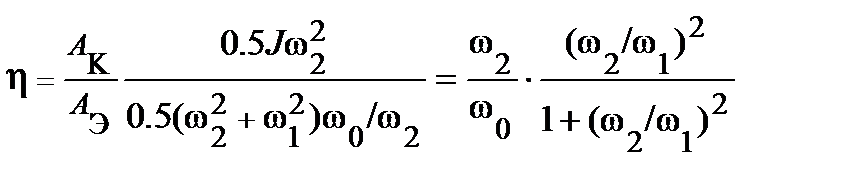. (13.3)

Так как на этапе регулирования потоком между значениями угловой скорости и потока должно выполняться соотношение ω₂/ω₁ = Ф₁/Ф₂, то выражение (13.3) переписывают в виде:

,

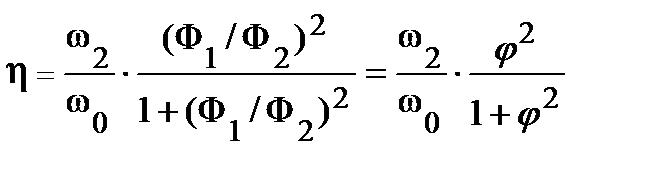где 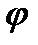- коэффициент форсировки потока.

Значение функции 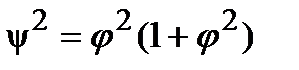при коэффициентах формировки по­тока φ=2-3 возрастает довольно быстро, однако дальнейшее увели­чение коэффициента форсировки (φ >3) не вызывает быстрого возраста­ния функции ψ (рис. 13.4,б). Поэтому в реальных системах запуска делают обычно φ=2.5-3 . Поскольку ω₂/ω₁= 0,7, то 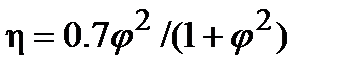. Полу­ченная зависимость η =f(φ) позволяет выбрать значение φ , эффективно влияющее на к. п. д.

Время запуска определяют как сумму интервалов времени при работе на первом и втором этапах пуска t_П= t₁+ t₂ - Значение t₁ определяют, используя выражение:

ω₁= ω₀₁ [1-eхр(-t₁/ T_M)],

где ;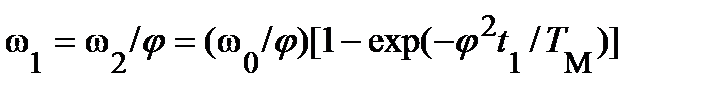

;

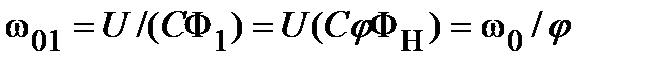Время t₂ запуска на втором этапе определяют из уравнения движения системы:

С I_АФ = J(dω/dt), где Ф = Ф_Н(ω₂/ ω); I_А=(U - С ω Ф/R_А) = const.

Используя законы изменения Ф и I_А в уравнении движения привода с учетом того, что U = С ω_оФ_н, получают

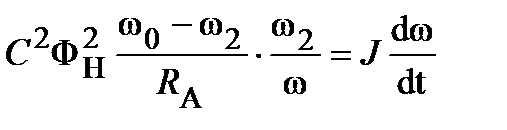или ,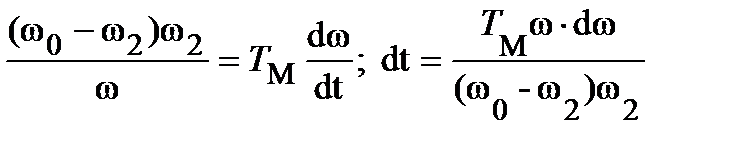

откуда

.

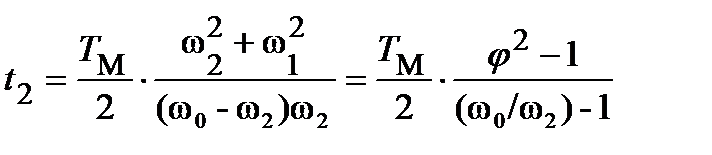При φ = 2 к.п.д. запуска η=0.56, время пуска t_П= t₁+ t₂= 1,17Т_М.

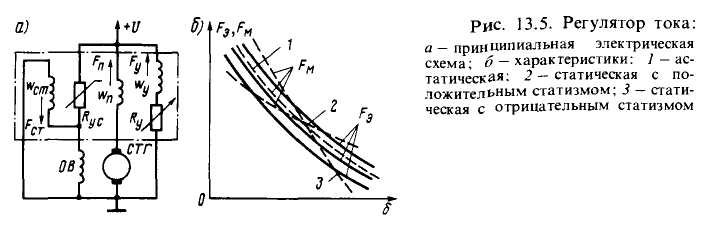
Для плавного изменения потока возбуждения стартера применяют угольный регулятор тока РУТ-600. Основной рабочей обмоткой регуля­тора тока является его последовательная (токовая) обмотка w_П (рис. 13.5, а), по которой проходит весь ток якоря стартера. В отличие от регулятора напряжения электромагнитная сила F_П последовательной обмотки сжимает угольный столб, а реакция пружины F_ПР ослабляет сжатие. Управляющая обмотка w_У служит для постройки регулятора на нужное значение тока якоря стартера; ее электромагнитная сила F, тоже сжимает угольный столб. Когда регулятор включен, любое отклонение тока якоря СТГ от значения, установленного при настройке, приводит к изменению силы F_П. В результате изменяются сжатие угольного столба и его сопротивление R_УС, ток возбуждения СТГ и его противо-э.д.с. Е=СωФ. Плотность и значение приращения противо-э.д.с. таковы, что их воздействие устра­няет отклонение тока (с определенной статической ошибкой) от его зна­чения, установленного при настройке. В системе запуска с плавным изме­нением потока возбуждения возможно возникновение неустойчивого ре­жима вследствие особенностей параметров регулятора. Точность стабили­зации тока в первую очередь определяется чувствительностью регулятора и цепи возбуждения, которую характеризуют коэффициенты передачи электромагнита к_ЭМ=(д F_Э/д i_p)₀, угольного столба К_УС=(д К_УС/дδ)₀ регуля­тора и К_В=( д i_В /д R_УС)₀ обмотки возбуждения (здесь i_Р = i_А+ w_Уi_У/w_П - суммарный ток электромагнита регулятора; δ - воздушный зазор).

С увеличением чувствительности регулирование приближается к аста­тическому, но уменьшается запас устойчивости системы. Учитывая, что характеристики реальных угольных регуляторов (рис. 13.5,б) близки к ас­татическим, не исключена опасность неустойчивой работы. Для повышения устойчивости в регулятор тока вводят ОСС по току возбуждения СТГ, используя специальную обмотку стабилизации w_CT, включенную на паде­ние напряжения на обмотке возбуждения. Сила электромагнита F_Э = F_П+ F_У- F_СТ.

13.6. Управление стартером многоступенчатым и плавным изменением напряжения

Многоступенчатое и плавное повышение напряжения на якоре стартера применяют часто. Запуск при многоступенчатом повышении напряжения используют для двигателей АИ-20, -24 от ВСУ ТГ-16, повышающей напряжение пятью ступенями до 60 В. Для запуска с плавным повышением напряжения до 70 В служат аэродромные источники. Запуск с многоступенчатым изменением напряжения применяют при питании стартера от генератора, напряжение которого повышают ступенями, ре­гулируя его ток возбуждения (рис. 13.6, а). Для этого в определенные моменты запуска в цепь обмотки электромагнита регулятора напряжения, входящего в систему запуска, в определенной последовательности вводят добавочные сопротивления.

Моменты перестройки регулятора и значения ступеней выбираются так, чтобы броски токов при переключениях были бы одинаковы и равны броску тока при пуске. Значения ступеней напряжения и моментов пе­реключения выбирают и из соображений приближения процесса запуска к оптимальному.

Для двигателя постоянного тока независимого возбуждения при М_С= const оптимальным является разгон при I_a=const. Значение тока якоря, а следовательно, и ускорения, выбирают по заданному значению потерь и с учетом ограничений, накладываемых на систему. В частности, на этом основании могут выбираться действующее или среднее значение тока при многоступенчатом изменении напряжения.

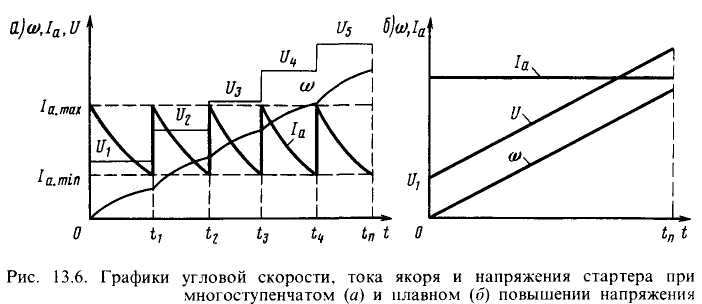
При многоступенчатом изменении напряжения стараются выполнить два условия: равенство бросков токов I_{a max} при переключениях на всех ступенях и равенство минимальных токов I_{a min} в конце каждой ступени.

Эти условия записывают в таком виде:

а) 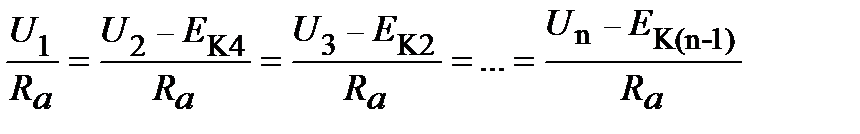(13.4)

или .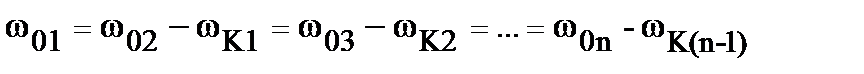

б) 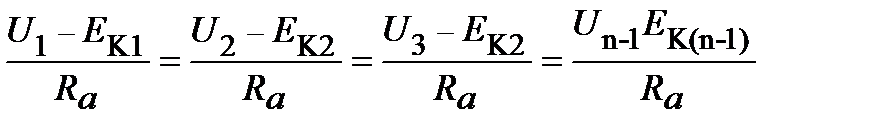(13.5)

или ,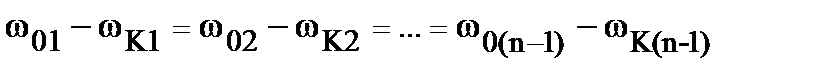

где ω_0i - угловая скорость идеального XX на i-й ступени.

Из выражения (13.4):

,

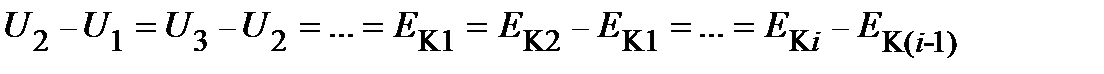Из уравнения (13.5):

.

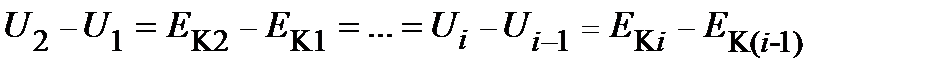Из условия равенства бросков тока при переключении ступеней следует, что приращение напряжения (в начале) каждой ступени должно быть равно приращению э.д.с. на каждой ступени:

.

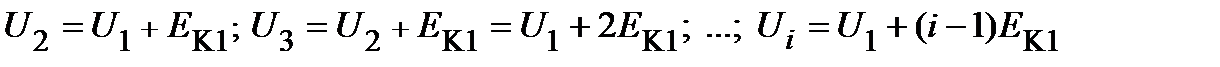Напряжение, подводимое к якорю стартера на всех ступенях, кроме первой, меняется n-1 равными ступенями:

∆U = E₁=(U_max- U₁):(n-1).

Время запуска равно сумме временных интервалов работы на каждой ступени пуска. Для i-й ступени:

; ,

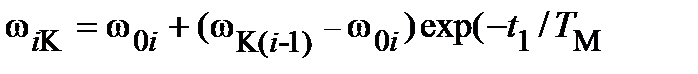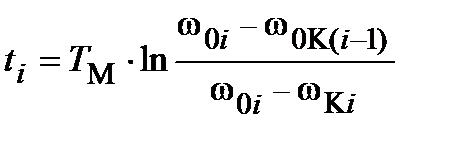где ω_iК - угловая скорость в конце i-й ступени.

Из условия равенства максимальных и минимальных значений тока якоря на ступенях пуска следует, что

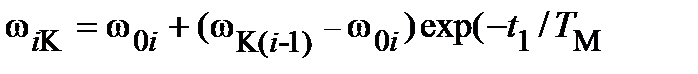
откуда .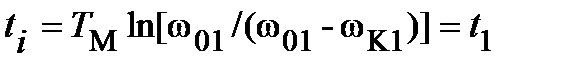

Время пуска t_П = nt₁.

В пределе пр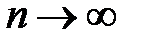и и 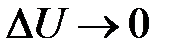получается пуск с плавным повыше­нием напряжения. Для этого напряжение также должно меняться плавно от некоторого начального значения U₁ (рис. 13.6,б).

Характер изменения угловой скорости системы стартер - авиадвигатель определится из уравнения СФ(U₁/ R_А)= J(dω/dt), откуда dω= (СФ/J)·(U₁/ R_А)dt и ω=[СФ/(J·R_А)]·[СФ/(СФ)]U₁t или

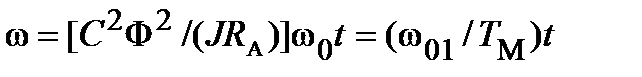. (13.6)

При условии I_А=U₁/ R_А=const угловая скорость растет по линейному закону во времени.

До конечной угловой скорости ω_К стартера время пуска

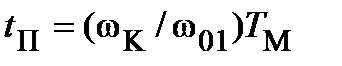(13.7)

Закон изменения напряжения при пуске находят из условия постоян­ства тока якоря в процессе пуска:

[U(t)-СωФ]/R_А= U/ R_А=I_A=const.

Заменяя в формуле (13.7) 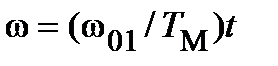, получают, что

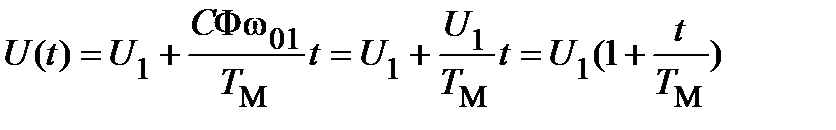. (13.8)

Из уравнения (13.8) следует, что при условии I_А=const напряжение меняется во времени по линейному закону. Учитывая, что и угловая скорость стартера во времени также меняется по линейному закону (см. уравнение 13.6), следует, что и напряжение также является линейной функцией угловой скорости. Зная количественную связь между временем и угловой скоростью, которая определяется выражением t =Т_М(ω/ω₀₁), на­ходят закон изменения напряжения в зависимости от угловой скорости:

.

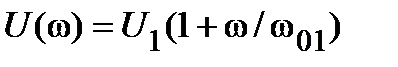Экономичность пуска определяется значением его к.п.д.: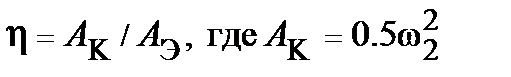

(здесь ω₂ - угловая скорость стартера при его отключении);

А_Э - расход электроэнергии при пуске 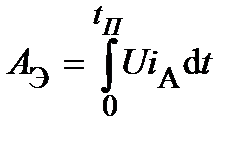. Подставляя в выражение для расхода электроэнергии при пуске выражения

,

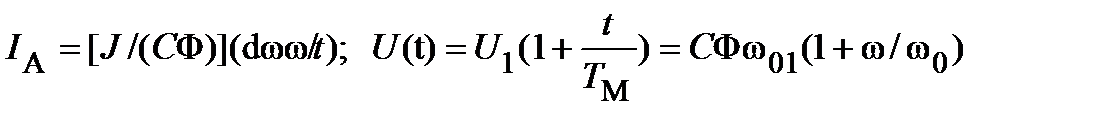получают .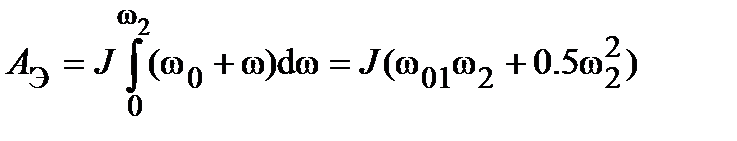

Подставив выражение расхода электроэнергии в формулу для к.п.д., определяют зависимость к.п.д. от величин, характеризующих запуск при линейном законе нарастания напряжения от угловой скорости

.

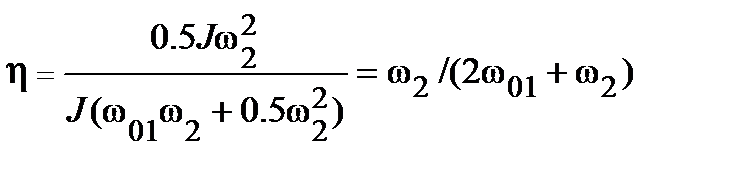При пренебрежении моментами статической нагрузки, полагая М_С=0 (или М_С=const), разгон системы СТГ-ГТД до заданной угловой ско­рости при постоянном потоке возбуждения и постоянном токе якоря является оптимальным переходным процессом.

Значение 1_А и dω/dt выбирают исходя из допустимых потерь за процесс разгона:

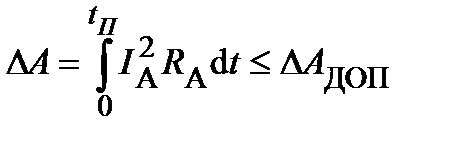
и ограничений, накладываемых на узлы системы по условиям работы (допустимые ускорения, допустимый ток якоря по условиям коммутации, допустимое значение напряжения на якоре стартера и т. д.).

Управление запуском плавным повышением напряжения - это наибо­лее совершенный способ управления стартером, позволяющий разогнать ГТД до заданной частоты вращения за минимальное время при задан­ных потерях и ограничениях. При учете моментов М_К и М_Т закон управ­ления получается сложнее. Из-за сложности его технической реализации в реальных системах производится запуск при постоянном токе якоря.

Глава 14