Производная произведения функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и
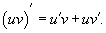
Производная частного функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
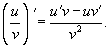
Производная суммы двух функций. 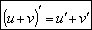
Вопрос 101. Дифференцирование сложной функции.
Вопрос 102. Производные для функций: , . , x e xx, cos , sin x a xx, ctg , tg ln , , arcctg , xx x x x a log , arccos arctg x , tg , arcsin xx
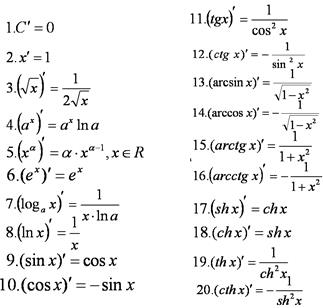
Вопрос 103 . Теорема о дифференцировании сложной функции.
Вопрос 104. Производные функций, заданных неявно и параметрически
Производная параметрически заданной функции
Если функция f задана параметрически
x = φ(t), y = ψ(t), α < t < β,
где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то
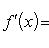
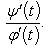
Производная неявно заданной функции
Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения
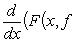
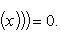
Вопрос 105 . Понятие дифференциала и формула для вычисления дифференциала функции.
Вопрос 106. Геометрический смысл дифференциала
П 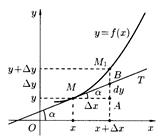 роведем к графику функции
роведем к графику функции 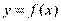 в точку
в точку 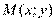 касательную
касательную 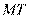 и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки 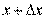 . На рисунке
. На рисунке 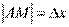 ,
, 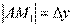 . Из прямоугольного треугольника
. Из прямоугольного треугольника 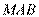 имеем:
имеем: 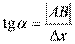 , т.е.
, т.е. 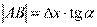 . Но, согласно геометрическому смыслу производной,
. Но, согласно геометрическому смыслу производной, 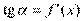 . Поэтому
. Поэтому 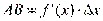 или
или 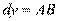 . Это означает, что дифференциал функции
. Это означает, что дифференциал функции 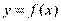 в
в 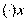 равен приращению ординаты касательной к графику функции в этой точке, когда
равен приращению ординаты касательной к графику функции в этой точке, когда 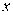 получает приращение
получает приращение 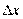 .
.
Вопрос 107. Угол между двумя кривыми
Вопрос 108. Физический смысл второй производной








