Первый замечательный предел

Дата: 2025-04-30; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

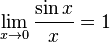
Определение

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Вопрос 84. Определение непрерывности функции в точке.

Вопрос 85. Определение приращения функции.

Определение: приращением аргумента называется разность х2 - х1, которую

обозначают символом ∆x (читается: дельта икс). Итак,

∆x = х2 - х1 или х2 = х1 + ∆x .

Приращение аргумента может быть как положительным, так и отрицательным.

Вопрос 86. Необходимое и достаточное условие непрерывности функции в точке.

Необходимое и достаточное условие непрерывности функции в точке

Функция y = f(x) непрерывна в точке х₀ тогда и только тогда, когда

Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.

Пусть функция f(x) определена в полуинтервале [x₀, x₀ + δ ).

Функция f(x) называется непрерывной справа в точке x₀, если существует односторонний предел

Пусть функция f(x) определена в полуинтервале (x₀ − δ, x₀].

Функция f(x) называется непрерывной слева в точке x₀, если существует односторонний предел

Вопрос 87. Классификация точек разрыва

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция 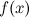определена в точке и ее окрестности;

2. существует конечный предел функции 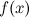в точке ;

3. это предел равен значению функции в точке , т.е.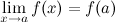

называется точкой разрыва функции.

Точка разрыва первого рода

Определение

Если в точке существуют конечные пределы 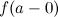и 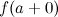, такие, что 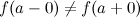, то точка называется точкой разрыва первого рода.

Точка разрыва второго рода

Определение

Если хотя б один из пределов 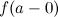или 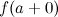не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции 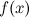в точке : 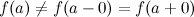или функция 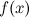не определена в точке , то точка называется точкой устранимого разрыва

Вопрос 88. Определение непрерывности функции на отрезке.

Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

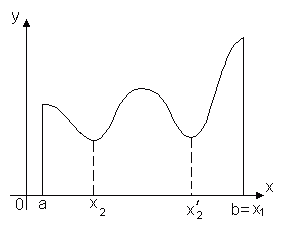Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁ Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂'.

Вопрос 89. Арифметические действия над непрерывными функциями

Вопрос 90. Теорема об устойчивости знака непрерывной функции

Вопрос 91. 1-ая теорема Больцано-Коши и ее геометрический смысл

Вопрос 92. Непрерывность сложной функции

Функция f(x) называется непрерывной в точке x₀, если .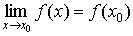

Вопрос 93. Определение производной функции y = f (x)

Вопрос 94. Геометрический смысл производной.

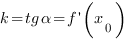Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Вопрос 95. Физический смысл первой производной

Вопрос 96. Уравнение нормали к графику функции y = f (x) в точке с абсциссой x=x₀

Вопрос 97. Уравнение касательной к графику функции y = f (x) в точке с абсциссой x₌х₀ .

Вопрос 98. Определение дифференцируемой в точке функции.

Пусть функция 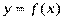определена в некоторой окрестности точки 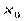. Если приращение 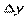функции 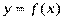можно представить в виде

,

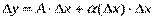где A – постоянное число в точке ;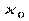

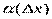- бесконечно малая функция при ,

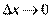то функция 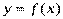называется дифференцируемой в точке .

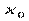Вопрос 99. Теорема о непрерывности функции, дифференцируемой в данной точке.

Если функция 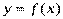дифференцируема в некоторой точке x=x_0, то она в этой точке непрерывна.

Вопрос 100. Производная суммы, произведения и частного двух функций.