74. 2-ой замечательный предел
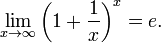
75. Теоремы о пределах суммы, произведения, частного двух последовательностей.
Теорема о пределе суммы и произведения. Пусть 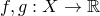 ,
, 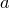 — предельная точка множества
— предельная точка множества 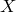 . Пусть
. Пусть
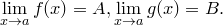
Тогда
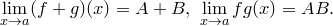
Доказательство. Возьмем произвольную последовательность 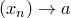
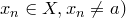 .Тогда
.Тогда 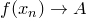 ,
, 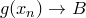 . По теореме о пределе суммы для последовательностей
. По теореме о пределе суммы для последовательностей
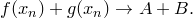
Но так как
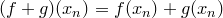
(из определения суммы функций), то
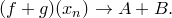
Доказательство второго утверждения аналогично.
Теорема о пределе частного. Пусть 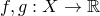 ,
, 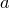 — предельная точка множества
— предельная точка множества 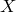 , пусть
, пусть 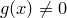 . Пусть
. Пусть
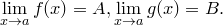
Тогда
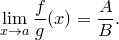
Доказательство аналогично доказательству теоремы о пределе суммы.
76. Предел функции.
Преде́лфу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
77. Односторонние пределы
Односторо́ннийпреде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́ннимпреде́лом (или преде́ломсле́ва) и правосторо́ннимпреде́лом (преде́ломспра́ва).
Число 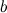 называется правым пределом функции
называется правым пределом функции 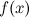 в точке
в точке  , если для
, если для 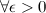
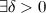 такое, что для любого
такое, что для любого 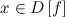 и
и 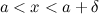 , выполняется неравенство
, выполняется неравенство 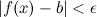 . Правый предел обозначается
. Правый предел обозначается 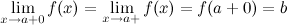
Число 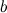 называется левым пределом функции
называется левым пределом функции 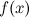 в точке
в точке  , если для
, если для 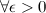
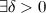 такое, что для любого
такое, что для любого 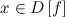 и
и 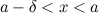 , выполняется неравенство
, выполняется неравенство 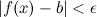 Левый предел обозначается
Левый предел обозначается 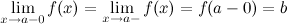
78. Предел функции при x стремится к бесконечности
79. Теоремы о пределах суммы, произведения, частного двух функций
ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций , то есть
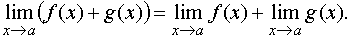
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть
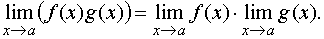
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть
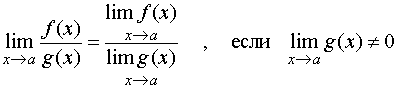
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля.
80. Бесконечно малые и бесконечно большие функции
Что тут сказать… Если существует предел 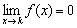 , то функция
, то функция 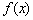 называется бесконечно малой в точке
называется бесконечно малой в точке 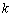 . не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке.
. не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке.
81. Сравнение бесконечно малых
Пусть a(x) и b(x) - две функции, бесконечно малые в точке x=a. Если
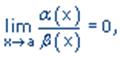
то говорят, что a(x) более высокого порядка малости, чем b(x)и обозначают a(x) =o(b(x)).
Если же
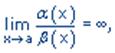
то b(x) более высокого порядка малости, чем a(x) ; обозначают b(x) =o(a(x)).
Бесконечно малые функции a(x) и b(x) называются бесконечно малыми одного порядка малости, если
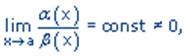
обозначают a(x) =const b(x) . И, наконец, если
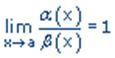
не существует, то бесконечно малые функции a(x) и b(x) несравнимы.
:: Сравнение бесконечно малых функций
Для того, чтобы сравнить две бесконечо малых функции, нужно вычислить предел их отношения.
Вопрос 82 . Эквивалентные б.м.ф., теорема о замене б.м.ф. на эквивалентные
Вопрос 83. Первый замечательный предел. Следствия.








