Всякий неравный нулю минор, порядок которого равен рангу матрицы, называется ее базисным минором.
Вопрос 47. Элементарные преобразования над матрицами
Элементарными преобразованиями матрицы называются следующие 4 операции:
1) перестановка двух строк (столбцов)
2) умножение строки (столбца) на число, неравное нулю
3) прибавление к строке (столбцу) другой строки ( другого столбца), умноженной (умноженного) на любое число
4) отбрасывание нулевой строки (нулевого столбца)
Вопрос 48. Теорема об элементарных преобразованиях
Ранг матрицы не меняется при ее элементарных преобразованиях.
Вопрос 49. Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Вопрос 50. Условия существования ненулевого решения у однородной системы mхn и системы nхn
Условия существования ненулевого решения у однородной системы mхn: однородная система mхn имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных.
Условия существования ненулевого решения у однородной системы nхn: однородная система nхn имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю.
Вопрос 51. Изображение на числовой оси множеств действительных чисел, заданных равенством и неравенством
52. Модуль действительного числа и его свойства
Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.
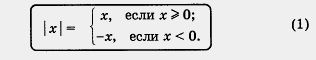
1. |а| 0.
2.|аb| =|a| |b|.
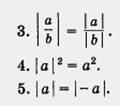
53. Геометрический смысл модуля числа и модуля разности двух чисел
Геометрический смысл – расстояние от точки с координатой Х на числовой прямой до начала координат.
Модуль разности – расстояние между соответствующими точками на числовой прямой.
54. Определение функции, определение графика функции
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
График функции — понятие в математике, которое даёт представление о геометрическом образе функции.
В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией: точка располагается (или находится) на графике функции тогда и только тогда, когда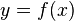 
55. Определение сложной и обратной функции, четной и нечетной функции. Тождества, вытекающие из существования обратной функции.
Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у).
Взаимно обратные функции
Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f.
Если функция g является обратной для функции f, то и функция является обратной для функции g.
Пару функций f и g называют взаимно обратными функциями.
График обратной функции
Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х.
Свойства взаимно обратных функций
Отметим некоторые свойства взаимно обратных функций.
1) Тождества. Пусть f и g – взаимно обратные функции. Тогда : f(g(y)) = у и g(f(x)) = х.
2) Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g.
3) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций.
4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой у = х.
Функция называется чётной, если справедливо равенство
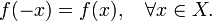
Функция называется нечётной, если справедливо равенство
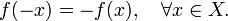
56. Элементарная функция
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из основных элементарных функций:
Степенная функция
Показательная функция
Логарифмическая функция
Тригонометрические функции
Обратные тригонометрические функции
57. Определение комплексного числа
Ко́мпле́ксныечи́сла— числа вида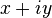 
, где 
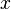и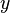 
— вещественные числа, 
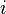— мнимая единица; то есть 
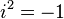. Множество всех комплексных чисел обычно обозначается 
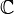— тесно связанный.
58. Алгебраическая форма комплексного числа, модуль и аргумент комплексного числа,
Алгебраическая форма
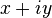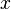Запись комплексного числа в виде , где и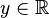 
,называется алгебраической формой комплексного числа.
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа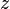 
обозначается 
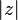и определяется выражением 
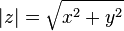. Часто обозначается буквами 
или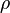 
Для любых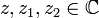 
имеют место следующие свойства модуля. :
1) 
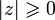, причём 
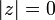тогда и только тогда, когда 
;
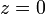2) 
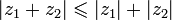(неравенство треугольника);
3) 
;
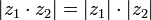4) 
.
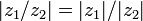Угол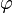 
(в радианах) радиус-вектора точки, соответствующей числу 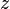, называется аргументом числа и обозначается 
.
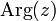59. Сложение, умножение и деление комплексных чисел
Сложение
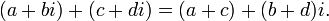
Умножение(не отличается от обычного)
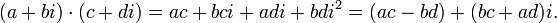
Деление
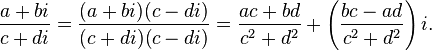
60. Главное значение аргумента комплексного числа.
Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла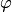 
для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функци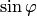й 
и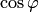 
.
Всякий угол, отличающийся от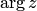 
на слагаемое, кратное 
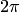, обозначается 
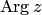и записывается равенством:
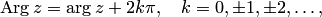
где 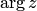— главное значение аргумента, 
.
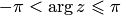61. Показательная форма комплексного числа.
Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:
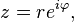
где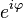 
— расширение экспоненты для случая комплексного показателя степени.
62. Тригонометрическая форма комплексного числа. Формула Эйлера.
Тригонометрическая форма
Если вещественную 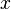и мнимую 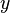части комплексного числа выразить через модуль 
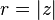и аргумент ( 
, 
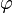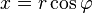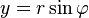), то всякое комплексное число 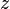, кроме нуля, можно записать в тригонометрической форме
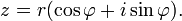
Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство:
,
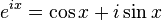где 
— основание натурального логарифма,
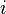— мнимая единица.
63. Комплексно сопряженные числа
Если комплексное число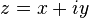 
, то число 
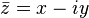называется сопряжённым (или комплексно сопряжённым) кZ.. На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
64. Геометрический смысл: операции сложения комплексных чисел, операции комплексного сопряжения, модуля разности двух комплексных чисел.
Геом. Смысл сложения комплексных чисел: если комплексные числа рассматривать как векторы на плоскости, то сложению комплексных чисел соответствует сумма векторов.
Операция комплексного сопряжения имеет простой геом. Смысл – отражение относительно оси ОХ.
То есть модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам
65. Возведение в степень комплексного числа (формула Муавра)
Эта формула помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
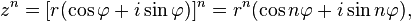
где — модуль, а 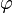— аргумент комплексного числа
66. Определение числовой последовательности
Числовая последовательность — это последовательность элементов числового пространства. Числовой последовательностью называется множество чисел, занумерованное натуральными числами nэN
67. Арифметические действия над последовательностями
Пусть даны последовательности {xn} и {yn}.
Произведением последовательности {хn} на число m назовем последовательность m·x1, m·x2, …, m·xn, ….
Суммой данных последовательностей назовем последовательность x1 + y1, x2 + y2, …, xn + yn, ….
Разностью – последовательность x1 − y1, x2− y2, …, xn− yn, …,
Произведением — последовательность x1·y1, x2·y2, … xn·yn,…
Частным — последовательность если все члены последовательности {yn} отличны от нуля.
Указанные действия над последовательностями символически записываются так:
– m·{ xn} = {m· xn}
– {xn} + { yn} = { xn + yn}
– {xn} - { yn} = { xn - yn}
– {xn} · { yn} = { xn · yn}
68. Ограниченные и неограниченные последовательности
В предположении о линейной упорядоченности множества элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностей.
Ограниченная сверху последовательность — это последовательность элементов множества , все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.
Неограниченная последовательность — это последовательность, которая не является ограниченной.
69. Бесконечно большие и бесконечно малые последовательности
Бесконечно малая последовательность — это последовательность, предел которой равен нулю.
Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.
70. Определение предела последовательности. Сходящаяся последовательность
Сходящаяся последовательность — это последовательность элементов множества , имеющая предел в этом множестве.
Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера.
Свойства сходящихся последовательностей
Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
Если последовательность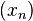 
сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность 
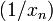, которая является ограниченной.
Сумма сходящихся последовательностей также является сходящейся последовательностью.
Разность сходящихся последовательностей также является сходящейся последовательностью.
Произведение сходящихся последовательностей также является сходящейся последовательностью.
Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
71. Определение убывающей числовой последовательности.
Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X(n+1) <Xn. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена.
72. Определение возрастающей числовой последовательности.
Последовательность (Xn) называется возрастающей, если для всех натуральных n выполняется следующее равенство X(n+1) >Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.
73. Теорема Вейерштрасса (достаточное условие сходимости последовательности).
Теорема Вейерштрасса об ограниченной возрастающей последовательности утверждает, что любая ограниченная возрастающая последовательность имеет предел, причем этот предел равен ее точной верхней грани.