Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида
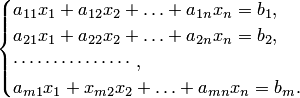
Числа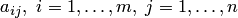 
называются коэффициентами системы; 
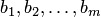— свободными членами, 
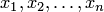— неизвестными. Количество 
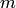уравнений в системе может быть меньше, больше или равно числу 
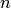неизвестных.
Система называется однородной, если все свободные члены равны нулю; в противном случае она называется неоднородной.
Решением системы называется упорядоченная совокупность 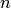чисел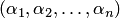 
такая, что после замены неизвестных 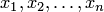соответственно числами 
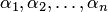каждое уравнение системы превращается в верное числовое равенство.
Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Две системы уравнений называются эквивалентными, если множество их решений совпадают
Вопрос 44. Матрица системы линейных уравнений, матричная форма записи системы
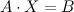Исходную Системой линейных алгебраических уравнений можно записать в матричном виде:
,
где матрица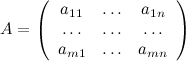 
называется матрицей системы, это матрица, составленная из коэффициентов при неизвестных; 
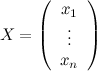- вектором-столбцом неизвестных, 
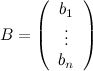- вектором-столбцом правых частей или свободных коэффициентов.
Вопрос 45. Правило Крамера
Системой однородных линейных уравнений называется система вида
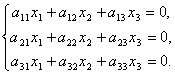
Ясно, что в этой случае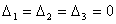 
, т.к. все элементы одного из столбцов в этих определителях равны нулю.
Так как неизвестные находятся по формулам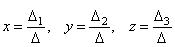 
, то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.
Вопрос 46. Минор к-ого порядка, ранг матрицы, базисный минор
Определитель, который образован элементами матрицы, стоящими на пересечении произвольно выбранных k строк и k столбцов, называется минором k-го порядка этой матрицы ( при этом минор 1-го порядка – это произвольный элемент данной матрицы).
Рангом матрицы называется наивысший порядок ее миноров, отличных от нуля (ранг нулевой матрицы полагается равным нулю). Ранг матрицы А обозначается символом r(А).