Обозначаются матрицы

Дата: 2025-04-30; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Равенство матриц

Две матрицы равны, если эти матрицы имеют одинаковые размеры, и все их соответствующие элементы совпадают.

Вопрос 37. Матрица-строка, матрица-столбец

Матрицей-строкой называется матрица размером 1хn, т.е. состоящая из одной строки.

Матрицей-столбцом называется матрица размером mх1, состоящая из одного столбца.

Вопрос 38. Нулевая, квадратная, треугольная, диагональная, единичная матрицы

Матрица 0, все элементы которой равны нулю, называется нулевой.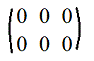

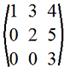Матрица размера nxn называется квадратной матрицей n-го порядка. Элементы а₁₁,а_22,…а_nn квадратной матрицы n-го порядка образуют её главную диагональ, а элементы ………….. – побочную диагональ.

Квадратная матрица называется треугольной, если все элементы, расположенные, ниже (или выше) главной диагонали равны нулю.

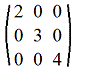
Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю.

Диагональная матрица называется единичной, если все элементы ее главной диагонали равны единице. Единичную матрицу обозначают буквой Е.

Вопрос 39. Операции над матрицами

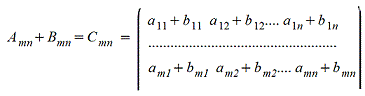
1. Сложение матриц - поэлементная операция

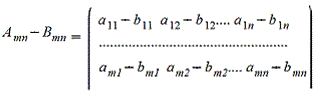
2. Вычитание матриц - поэлементная операция

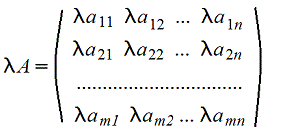
3. Произведение матрицы на число - поэлементная операция

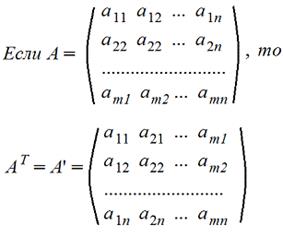
4. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

Вопрос 40. Определитель квадратной матрицы, треугольной матрицы, единичной матрицы, произведения матриц

Вопрос 41. Обратная матрица: определение, условие существования, формула для вычисления

Матрица А^-1 называется обратной (к) квадратной матрице А, если АА^-1=А^-1А=Е

Для того чтобы для матрицы А существовала обратная матрица, необходимо и достаточно, чтобы А была невырожденной.

Формула для вычисления обратной матрицы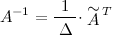

Вопрос 42. Решение матричных уравнений

С помощью обратной матрицы легко решается линейное матричное уравнение вида АХ=В, где А – невырожденная матрица порядка n, В – матрица размера nxk, а Х – искомая матрица. Умножая данное уравнение на А^-1 слева, получим:

А^-1(АХ)=А^-1В => (А^-1А)Х=А^-1В => ЕХ=А^-1В => Х=А^-1В

То что матрица Х действительно является решением данного уравнения, легко проверяется путем подстановки ее в данное уравнение:

А(А^-1В)=( А^-1А)В=ЕВ=В,

а его единственность следует из единственности обратной матрицы.

Аналогично, решение уравнения YA=B имеет вид Y=BА^-1.

Вопрос 43. Система линейных уравнений, однородная и неоднородная система, решение системы, совместная и несовместная система, эквивалентные системы