Свойства операции сложения: для любых векторов a,b,c
1) a+b = b+a
2) (a+b)+c = a+(b+c)
3) a+0 = a
4) a+(-a) = 0
Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.
Свойства умножения вектора на число:
Свойство 1. k(a + b) = ka + kb.
Свойство 2. (k + m)a = ka + ma.
Свойство 3. k( ma) = ( km)a.
Вопрос 13. Коллинеарные и компланарные векторы
Векторы называются коллинеарными, если они лежат на параллельных прямых. Векторы коллинеарны тогда и только тогда, когда, будучи приложенными к одной точке они лежат на одной прямой.
Векторы называются компланарными, если они лежат в параллельных плоскостях. Векторы компланарны тогда и только тогда, когда, будучи приложенными к одной точке они лежат в одной плоскости.
Вопрос 14. Проекция вектора на ось, проекция вектора на вектор, вычисление проекций
Проекция вектора а на ось L называется длина его составляющей по оси L , взятая со знаком «+», если направления составляющей по оси L совпадают, и со знаком «–», то эти направления противоположны.
Под проекцией вектора а на вектор b (не равный нулю) понимается проекция вектора а на (любую) ось, имеющу направление вектора b.
Вопрос 15. Координаты вектора
Вопрос 16. Единичный вектор (орт)
Вектор, длина которого равна единице, называется единичным вектором ( или ортом ). Единичный вектор, имеющий направление данной оси L (данного вектора а), называется ортом оси L (ортом вектора а)
Вопрос 17. Радиус-вектор точки
Пусть М – произвольная точка координатного пространства Oxyz. Радиус-вектора точки М называется вектор r=ОМ.
Вопрос 18. Линейные операции над векторами в координатной форме
Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.
1. Равные векторы имеют равные координаты (в одном и том же базисе).
2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.
3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.
4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.
Вопрос 19. Условие коллинеарности двух векторов
Два вектора коллинеарные, если отношения их координат равны.
Два вектора коллинеарные, если их векторное произведение равно нулю.
Вопрос 20. Направляющие косинусы произвольного вектора и орта
Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.
Если в пространстве задан вектор 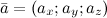 , то его направляющие косинусы вычисляются по формулам:
, то его направляющие косинусы вычисляются по формулам:
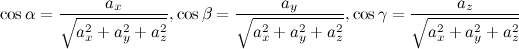
Сумма квадратов направляющих косинусов равна единице.
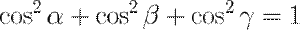
Вопрос 21. Скалярное произведение векторов и его свойства, скалярное произведение в координатной форме
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то угол между ними не определён, а скалярное произведение считается равным нулю. Скалярное произведение векторов 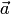 и
и 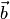 обозначается
обозначается
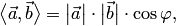
где 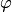 — величина угла между векторами
— величина угла между векторами 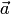 и
и 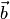 .
.
Скалярное произведение вектора самого на себя 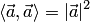 называется скалярным квадратам.
называется скалярным квадратам.
Свойства скалярного произведения: 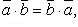
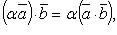
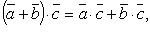
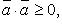
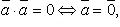
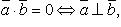
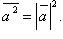
Вопрос 22. Ортогональные векторы, условие ортогональности двух векторов
Два вектора называются ортогональными, если они перпендикулярны ( угол между ними равен П/2 ) или если хотя бы один из них равен нулю.
Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Вопрос 23. Правая тройка векторов
Тройка векторов 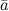 ,
, 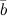 и
и 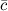 называется левой, если поворот от вектора
называется левой, если поворот от вектора 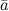 к вектору
к вектору 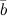 , видимый с конца третьего вектора
, видимый с конца третьего вектора 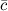 , осуществляется по ходу часовой стрелки рис. 1
, осуществляется по ходу часовой стрелки рис. 1
Тройка векторов 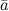 ,
, 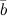 и
и 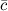 называется правой, если поворот от вектора
называется правой, если поворот от вектора 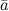 к вектору
к вектору 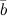 , видимый с конца третьего вектора
, видимый с конца третьего вектора  , осуществляется против хода часовой стрелки рис. 2
, осуществляется против хода часовой стрелки рис. 2
Вопрос 24. Векторное произведение и его свойства, векторное произведение в координатной форме
Вектор 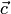 называется векторным произведением неколлинеарных векторов
называется векторным произведением неколлинеарных векторов 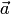 и
и 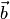 , если:
, если:
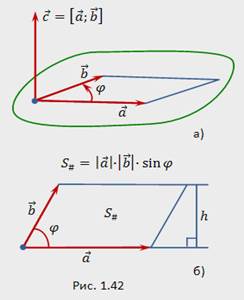
1) его длина равна произведению длин векторов 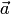 и
и 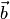 на синус угла между ними:
на синус угла между ними: 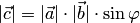 (рис.1.42);
(рис.1.42);
2) вектор 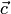 ортогонален векторам
ортогонален векторам 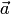 и
и 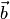 ;
;
3) векторы 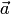 ,
, 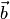 ,
, 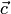 (в указанном порядке) образуют правую тройку.
(в указанном порядке) образуют правую тройку.
Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Векторное произведение обозначается 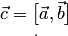 (или
(или 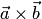 ).
).
Векторное произведение в координатной форме
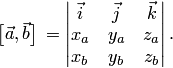
Вопрос 25. Направляющий и нормальный векторы данной прямой
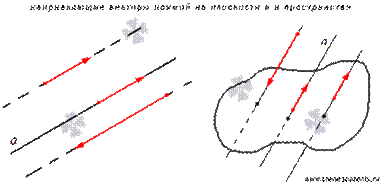 Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.
Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.
Нормальный вектор прямой - это любой ненулевой вектор, лежащий на любой прямой перпендикулярной данной.
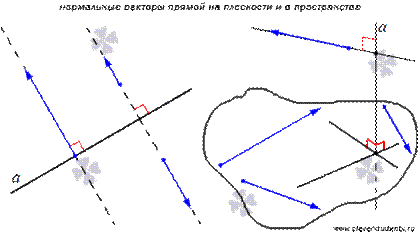
Вопрос 26. Виды уравнений прямой на плоскости
1) векторное: 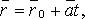
2) параметрическое: 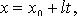
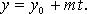
3) каноническое: 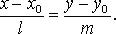
4) параллельной оси у («вертикальной»): x=a
5) параллельной оси х («горизонтальной»): y=b
6) уравнение прямой по точке и угловому коэффициенту: 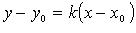 или
или 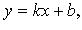
7) уравнение прямой по двум точкам: 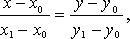
8) проходящей через данную точку данным нормальным вектором: А(х-х0)+(у-у0)=0
9) общее: Ах+Ву+С=0
Вопрос 27. Формула расстояния от точки до прямой, формулы вычисления угла между прямыми
Расстояние от точки до прямой: 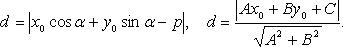
Угол между двумя прямыми: 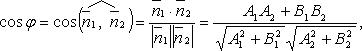
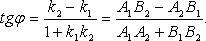
Вопрос 28. Условия параллельности и перпендикулярности двух прямых
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями y = k1x + B1, y = k2x + B2, с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2.
б) Для случая, когда прямые заданы уравнениями в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
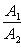
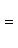
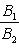

Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями y = k1x + B1, y = k2x + B2, с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
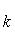
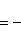
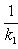

Это условие может быть записано также в виде: k1k2 = -1.
б) Если уравнения прямых заданы в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства:
A1A2 + B1B2 = 0.
Вопрос 29. Виды уравнений плоскости
1) уравнение плоскости, проходящей через данную точку с данным нормальным вектором: 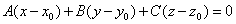
2) общее уравнение плоскости: 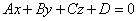
3) нормальное уравнение плоскости: 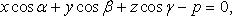
Вопрос 30. Формула расстояния от точки до плоскости, формулы вычисления угла между плоскостями
Расстояние от точки до плоскости: 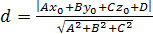
Если две плоскости 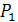 и
и 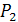 заданы общими уравнениями вида:
заданы общими уравнениями вида:
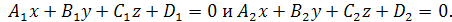
Под углом между плоскостями 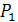 и
и 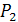 понимается один из двугранных углов, образованных этими плоскостями.
понимается один из двугранных углов, образованных этими плоскостями.
Очевидно, что угол между 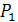 и
и 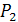 равен углу между их нормалями, то есть между векторами
равен углу между их нормалями, то есть между векторами 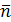 1
1 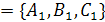 и
и 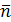 2
2 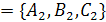 .
.
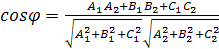 Из формулы
Из формулы 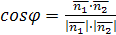 получаем, что косинус угла между плоскостями
получаем, что косинус угла между плоскостями 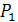 и
и 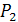
равен
Вопрос 31. Условия параллельности и перпендикулярности двух плоскостей
Условие параллельности плоскостей заключается в параллельности нормалей 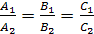 , а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:
, а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: 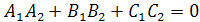 .
.
Вопрос 32. Виды уравнений прямой в пространстве
1) векторное: 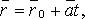
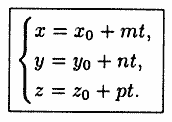
2) параметрическое:
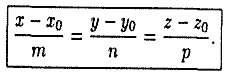
3) каноническое:
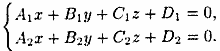
4) общее:
Вопрос 33. Кривые второго порядка: эллипс, гипербола, парабола (определения и их канонические уравнения)
Линиями второго порядка являются: эллипс (в частности окружность), гипербола, парабола, две прямые, одна прямая, одна точка и, наконец, линия не содержащая ни одной точки(т.е. просто пустое множество).
Общий вид уравнения второй степени с двумя переменными х и у:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
1) Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых до двух данных точек этой плоскости (называемых фокусами), есть величина постоянная (большая, чем расстояние между фокусами)
Каноническое уравнение эллипса: 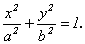
2) Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых до двух данных точек этой плоскости (называемых фокусами), есть величина постоянная ( положительная и меньшая, чем расстояние между фокусами).
Каноническое уравнение гиперболы: 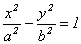
3) Параболой называется множество всех точек плоскости, каждая из которых равноудалена от данной точки этой плоскости (называемой фокусом) и данной прямой, лежащей в этой плоскости и не проходящей через фокус ( она называется директрисой)
Каноническое уравнением параболы: y² = 2px
Вопрос 34. Уравнение поверхности в пространстве, явное и неявное
Уравнение F(x, у, z) = 0 называется уравнением данной поверхности в пространстве xyz, если эта поверхность есть множество точек этого пространства, координаты которых удовлетворяют этому уравнению.
z=f(x,y) – явное уравнение поверхности в пространстве xyz ( уравнение графика функции f(x,y)).
F(x,y,z)=0 – неявное уравнение поверхности в пространстве xyz.
Вопрос 35. Уравнение сферы
Уравнение сферы с центром A (a; b; c) и радиусом R имеет вид:
(x – a)2 + (y – b)2 + (z – c)2 = R2.
Уравнение сферы радиуса r с центром в начале координат: 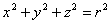
Вопрос 36. Матрица, ее элементы, обозначение, равенство матриц
Матрицей размера 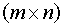 называется прямоугольная таблица, составленная из
называется прямоугольная таблица, составленная из 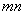 чисел (
чисел ( 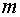 строк,
строк, 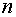 столбцов).
столбцов).
Числа a i,j, входящие в состав матрицы, называются ее элементами. Здесь i — номер строки матрицы, j — номер столбца матрицы.









