Минором данного элемента определителя называется определитель, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Вопрос 1. Формулы расстояния между двумя точками на прямой, на плоскости, в пространстве.
на прямой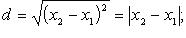 
на плоскости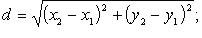 
в пространстве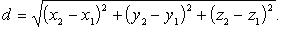 
Вопрос 2. Деление отрезка в заданном отношении, деление отрезка пополам
Деление отрезка в данном отношении
на прямой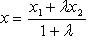 
;
на плоскости ,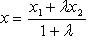 
;
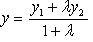в пространстве , ,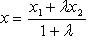 
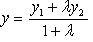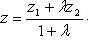
Середина отрезка
на прямой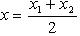 
;
на плоскости ,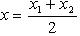 
;
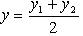в пространстве , ,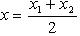 
.
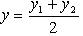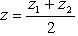Вопрос 3. Уравнение данной линии на плоскости, явное и неявное уравнение линии
Уравнение F(x,y)=0 называется уравнением данной линии на плоскости xy, если эта линия есть множество всех точек этой плоскости, координаты которой удовлетворят этому уравнению.
y=f(x) – явное уравнение линии на плоскости xy. ( y=kx+b )
F(x,y)=0 – неявное уравнение линии на плоскости xy. ( kx-y+b=0 )
Вопрос 4. Уравнение окружности с центром в точке (a, b) и радиусом R
(x — a)2+(y — b)2 = R2
Вопрос 5. Полярная система координат, полярные координаты точки, уравнение линии в полярных координатах.
Полярная система координат на плоскости — это совокупность точки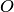 
, называемой полюсом, и полупрямой 
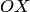, называемой полярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор 
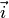, приложенный к точке 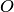, длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси.
Положение точки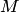 
в полярной системе координат определяется расстоянием 
(полярным радиусом) от точки 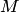до полюса (т.е. 
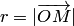)и углом 
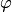(полярным углом) между полярной осью и вектором 
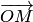. Полярный радиус и полярный угол составляют полярные координаты точки 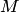, что записывается в виде 
.
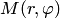Вопрос 6. Параметрические уравнения линии на плоскости
Вопрос 7. Определители второго и третьего порядка
Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
.
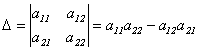Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
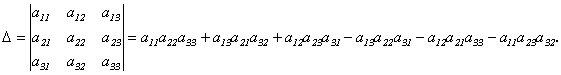
Вопрос 8. Свойства определителей
1) При транспонировании определитель не меняется
2) При перестановке двух строк определитель меняет знак
3) Если каждый элемент некоторой строки определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в каждом из которых элементы соответствующей строки равны соответствующим слагаемым, а остальные строки – те же, что и в данном определителе.
4) Общий множитель всех элементов одной строки можно вынести за знак определителя.
5) Если все элементы некоторой строки определителя равны нулю, то он равен нулю (короче: определитель с нулевой строкой равен нулю)
6) Если две строки определителя одинаковы, то он равен нулю.
7) Если соответствующие элементы двух строк определителя пропорциональны то он равен нулю (короче: если две строки определителя пропорциональны, то он равен нулю)
8) Если к элементам некоторой строки определителя прибавить соответствующие элементы другой его строки, умноженные на одно и тоже число (любое), то определитель не изменится (короче: если к некоторой строке определителя прибавить другую его строку, умноженную на некоторое число, то определитель не изменится)
9) Определитель равен сумме произведений элементов любой его строки на их алгебраическое дополнения.
10) Сумма произведений элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой его строки равна нулю.
Вопрос 9. Минор и алгебраическое дополнение данного элемента
Минором данного элемента определителя называется определитель, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Алгебраическим дополнением А ij элемента а ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
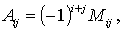
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Вопрос 10. Вектор, длина вектора, одинаковое и противоположное направление двух векторов, равенство двух векторов.
Вектором называется направляющий отрезок.
Длиной (модулем) вектора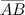 
называется неотрицательное число, равное расстоянию между его началом и концом, то есть длина вектора - это длина отрезка 
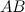. Длина 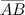обозначается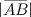 
Если вектор задан своими координатами: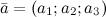 
, то его длина находится по формуле:
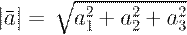
Два вектора имеют одинаковые направления (противоположные направления), если они лежат на параллельных прямых и направлены в одну сторону (противоположные стороны).
Два вектора называются равными, если они имеют одинаковые длины и одинаковые направления.
Вопрос 11. Свободный вектор, нулевой вектор
Два вектора называются равными, если они:
а) коллинеарны, одинаково направлены;
б) имеют равные длины.
Все нулевые векторы считаются равными друг другу.
Это определение равенства векторов характеризует так называемые свободные векторы. Данный свободный вектор можно переносить, не меняя его направления и длины, в любую точку пространства (откладывать от любой точки), при этом будем получать векторы, равные данному. Таким образом, свободный вектор определяет целый класс равных ему векторов, отличающихся только точкой приложения. Далее будут рассматриваться, как правило, свободные векторы, при этом слово "свободные" будет опускаться.
Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю. Если длина вектора положительна, то его называют ненулевым. Ненулевой вектор можно определить также как направленный отрезок, т.е. отрезок, у которого одна из ограничивающих его точек считается первой (началом вектора), а другая — второй (концом вектора). Направление нулевого вектора, естественно, не определено.
Вопрос 12. Линейные операции над векторами и их свойства
Сумма двух векторов a и b называется вектор a+b, который определяется по «правилу треугольника»
Сумму двух векторов можно находить по «правилу параллелограмма»