Восьмеричная система счисления
Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:
0, 1, 2, 3, 4, 5, 6, 7.
Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.
Перевод чисел из восьмеричной системы в двоичную и обратно
Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой.
| 08 = 0002 | 48 = 1002 |
| 18 = 0012 | 58 = 1012 |
| 28 = 0102 | 68 = 1102 |
| 38 = 0112 | 78 = 1112 |
Примеры.
25638 = 010 101 110 0112 =101011100112.
10011012 = 001 001 1012 = 1158.
Методические материалы для лабораторного занятия №1
Тема лабораторного занятия: Системы счисления. Измерение информации.
Количество часов: 2.
Примеры с решениями
1. Перевод из p -ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде
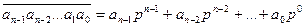 .
.
111001102 = 1∙27 + 1∙26 + 1∙25 + 0∙24 + 0∙23 + 1∙22 + 1∙21 + 0∙20 = 128 + 64 + 32 + 4 + 2 = 23010.
24015 = 2∙53 + 4∙52 + 0∙51 + 1∙50 = 250 + 100 + 0 + 1 = 351.
2. Перевод из 10-ичной системы в p -ичную.
2.1 9810 → Х2.
Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.
1) 98 : 2 = 49. Остаток — 0.
2) 49 : 2 = 24. Остаток — 1.
3) 24 : 2 = 12. Остаток — 0.
4) 12 : 2 = 6. Остаток — 0.
5) 6 : 2 = 3. Остаток — 0.
6) 3 : 2 = 1. Остаток — 1.
Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 9810 = 11000102.
2.2 239110 → Х16.
Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.
1) 2391 : 16 = 149. Остаток — 7.
2) 149 : 16 = 9. Остаток — 5.
Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 239110 = 95716.
2.3 1216510 → Х2.
Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.
1216510 = 276058 = 010 111 110 000 101 = 10111110000101.
3. Определение основания системы счисления p .
Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?
Решение. Надо определить основание системы счисления p. Так как мы знаем, что пальцев на ногах всего 1010, то 12p=1∙p+2 = 1010. Отсюда получаем уравнение p + 2 = 10 Û p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 248 = 2∙8+4 = 2010, а на ногах — 128 = 1∙8+2 = 1010.
ЗАДАНИЯ
1. Переведите следующие двоичные числа в десятичную систему счисления.
| а) 1002; | б) 1111002; | в) 11012; | г) 111112; | д)10000002. |
2. Переведите следующие десятичные числа в двоичную систему счисления.
| а) 1710; | б) 2010; | В) 3610; | г) 30010; | д) 1511210. |
3. Запишите текущий год в двоичной системе счисления.
4. Запишите в троичной системе счисления год своего рождения.
5. Составьте таблицу, в которой перечислены все десятичные, двоичные и шестнадцатеричные числа от 010 до 3210.
6. Составьте таблицу сложения размером 16 ´ 16 для восьмеричной системы счисления (строки и столбцы соответствуют восьмеричным цифрам от 0 до 7).
7. Решите следующие задачи:
1) Один иностранец из государства, где окончательно победила компьютерная революция, хвастал в письме одной девушке, что зарабатывает 110 000 долларов в месяц, что апартаменты у него общей площадью 10 100 кв. м, и счет в банке — 100 000 000 долларов. Девушка была с умом и поняла, что все это в двоичной системе. Сколько же это на самом деле?
2) Представьте себе, что вы договорились продать фирме из государства Хексландия партию модемов — 1000 штук по 50 долларов. А в этой стране тоже победила компьютерная революция, правда с человеческим лицом — там принята шестнадцатеричная система счисления. У них ходит своя валюта — хексы. Курс хекса к доллару 1:1. Человек из этой фирмы, недавно иммигрировавший в Хексландию, расплатился с вами купюрами, изображенными на Рис. 3, которые вы затем спокойно меняете на доллары. Какова ваша неожиданная дополнительная прибыль?
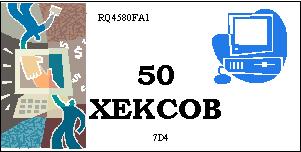
Рис. 3. Купюра в Хексландии
3) Как-то раз попали наши путешественники в одну далекую страну и разговорились с одним почтенным отцом семейства. Много детей, рассказал он, у него — 20 сыновей и 12 дочерей. Всего детей — 102, а лет ему — 1200. Сколько у него детей и каков его возраст? Указание. См. пример 3.
8. Чему равно наибольшее неотрицательное целое число, кодируемое 8 битами?
9. Пересчитайте в мегабайты: 10240 Кб, 1024000 Кб, 10 Гб, 1000 Гб.
Методические рекомендации по СРСП №1








