Классификация информации
Классификация – система распределения объектов (предметов, явлений, процессов, понятий) по классам в соответствии с определенным признаком.
Под объектом понимается любой предмет, процесс, явление материального или нематериального свойства. Система классификации позволяет сгруппировать объекты и выделить определенные классы, которые будут характеризоваться рядом общих свойств.
Классификация объектов – это процедура группировки на качественном уровне, направленная на выделение однородных свойств. Применительно к информации как к объекту классификации выделенные классы называют информационными объектами.
Свойства информационного объекта определяются информационными параметрами, называемыми реквизитами. Реквизиты представляются либо числовыми данными, например вес, стоимость, год, либо признаками, например цвет, марка машины, фамилия.
Реквизит – логически неделимый информационный элемент, описывающий определенное свойство объекта, процесса, явления и т.п.
Классификатор — систематизированный свод наименований и кодов классификационных группировок.
При классификации широко используются понятия классификационный признак и значение классификационного признака, которые позволяют установить сходство или различие объектов. Возможен подход к классификации с объединением этих двух понятий в одно, названное как признак классификации. Признак классификации имеет также синоним основание деления.
Пример. В качестве признака классификации выбирается возраст, который состоит из трех значений: до 20 лет, от 20 до 30 лет, свыше 30 лет. Можно в качестве признаков классификации использовать: возраст до 20 лет, возраст от 20 до 30 лет, возраст свыше 30 лет.
Разработаны три метода классификации объектов: иерархический, фасетный, дескрипторный. Эти методы различаются разной стратегией применения классификационных признаков.
Иерархическая система классификации.
Иерархическая система классификации (Рис. 1) строится следующим образом:
q исходное множество элементов составляет 0-й уровень и делится в зависимости от выбранного классификационного признака на классы (группировки), которые образуют 1-й уровень;
q каждый класс 1-го уровня в соответствии со своим, характерным для него классификационным признаком делится на подклассы, которые образуют 2-й уровень;
q каждый класс 2-го уровня аналогично делится на группы, которые образуют 3-й уровень, и т.д.
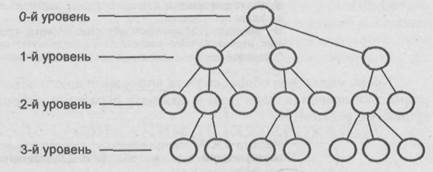
Рис. 1. Иерархическая система классификации
Пример. Поставлена задача — создать иерархическую систему классификации для информационного объекта «Студент», которая позволит классифицировать информацию обо всех студентах по следующим классификационным признакам: факультет, на котором он учится, возрастной состав студентов, пол студента, для женщин — наличие детей.
Система классификации представлена на Рис. 2 и будет иметь следующие уровни; 0-й уровень. Информационный объект «Студент»;
1-й уровень. Выбирается классификационный признак – название факультета, что позволяет выделить несколько классов с разными названиями факультетов, в которых хранится информация обо всех студентах.
2-й уровень. Выбирается классификационный признак — возраст, который имеет три градации: до 20 лет, от 20 до 30 лет, свыше 30 лет. По каждому факультету выделяются три возрастных полкласса студентов.
3-й уровень. Выбирается классификационный признак — пол. Каждый подкласс 2-го уровня разбивается на две группы. Таким образом, информация о студентах каждого факультета в каждом возрастном подклассе разделяется на две группы — мужчин и женщин.
4-й уровень. Выбирается классификационный признак — наличие детей у женщин: есть, нет.
Созданная иерархическая система классификации имеет глубину классификации, равную четырем.
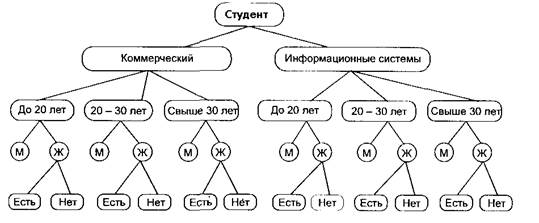
Рис. 2. Пример иерархической системы классификации для информационного объекта «Студент»
Измерение информации
Рассмотрим два способа измерения информации.
Первый способ отражает вероятностный подход к измерению информации.
Рассмотрим некоторый алфавит из N символов, где pi (i = 1, 2, ..., N) - вероятность выбора из этого алфавита i-ой буквы для описания (кодирования) некоторого состояния объекта. Каждый такой выбор уменьшит степень неопределенности в сведениях об объекте и, следовательно, увеличит количество информации о нем. Для определения среднего значения количества информации, приходящейся в данном случае на один символ алфавита, применяется формула
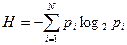 .
.
В случае равновероятных выборов pi = 1/N. Подставляя это значение в исходное равенство, мы получим
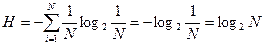 .
.
Пример. Пусть из набора 32 возможных чисел необходимо выбрать одно определенное число, получая на каждую попытку ответ «да» или «нет». Воспользуемся приведенной выше формулой, чтобы узнать то количество попыток, которое гарантирует нам отгадку нужного числа, т.е. количество информации, необходимое нам для выбора задуманного числа: Н = log2N = log232 = 5.
Рассмотрим еще одну задачу, решение которой связано с вероятностным подходом к измерению количества информации: кодовый замок сейфа должен включать не менее 1000 уникальных комбинаций. Сколько двухпозиционных переключателей необходимо включить в его конструкцию? Решение: Н = log21000. Н не является целым числом. Для гарантированного получения 1000 уникальных комбинаций заменим 1000 на 1024 - ближайшую к нему степень числа 2. log21024 = 10. Ответ: в конструкцию необходимо включить 10 двухпозиционных переключателей.
Второй способ, так называемый объемный. При алфавитно-цифровом представлении информации любое слово, являющееся последовательностью символов, становится информацией. Число символов в слове называется его длиной. Каждый новый символ увеличивает количество информации, представленной последовательности символов выбранного алфавита. Для измерения количества информации надо выбрать соответствующий эталон. Эталоном для подсчета количества информации, представленной последовательностью символов, логично считать слово минимальной длины, то есть состоящее из одного символа. Количество информации, содержащееся в слове из одного символа, принимают за единицу. Если мы конструируем сообщения, используя двузначный алфавит из двух цифр 0 и 1, то величина способная принимать два различных значения (0 и 1), становится эталонной единицей количества информации, называемой бит (binary digit- двоичный разряд).
В общей теории информации в качестве эталона меры для нее выбирается некоторый абстрактный объект, который может находиться в одном из двух состояний (например, включен / выключен, да / нет, 0 / 1 и т. п.), или, как еще говорят, бинарный объект. Говорят, что такой объект содержит информацию в 1 бит. Данный метод измерения информации во многом был предопределен возможностями ее хранения в различных технических устройствах, где на элементарном уровне информация запоминается с помощью магнитно-электрических устройств, которые могут находиться в одном из двух возможных состояний. Данное решение позволяет гармонично связать методы измерения информации с бинарной (двоичной) организацией системы ее хранения.
Сравнивая с эталоном, можно установить объем информации, содержащейся в слове, записанном в том же двузначном алфавите. Но при представлении информации в виде последовательности слов, составленных из символов двоичного алфавита, становится невозможным раскодирование, то есть понимание полученной информации. Понять ее можно только при условии наличия соглашения о фиксированной длине последовательностей из 0 и 1, составляющих слово в представленной информации. Такой длиной стали считать восемь символов (нулей и единиц) — 8 бит. Величина количества информации в 8 бит называется байтом. При работе с большими объемами информации для подсчета ее количества удобнее пользоваться более крупными единицами. Например, обозначают:
1 килобайт (Кбайт) = 1024 байт = 210 байт,
1 мегабайт (Мбайт) = 1024 Кбайт = 220 байт,
1 гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
В десятичной системе счисления единица измерения - дит (десятичный разряд).
Пример. Сообщение в двоичной системе в виде двоичного кода 10111011 имеет объем данных VД= 8 бит = 1 байт. Сообщение в десятичной системе 275903 имеет объем данных VД=6 дит.
КОДИРОВАНИЕ информации
Код — это правило отображения одного набора объектов или знаков в другой набор знаков без потери информации. При этом можно всегда однозначно возвратиться к прежнему набору объектов или знаков.
Кодирование — это представление, моделирование одного набора знаков другим с помощью кода.
Кодовая таблица — это соответствие между набором знаков и их кодами, обычно разными числами.
В компьютерной технике используется двоичное кодирование, использующее алфавит из двух символов {0,1}. Любая обработка информации компьютером оказалась возможной из-за естественного пребывания токопроводящих элементов компьютера только в одном из двух состояний, каждое из которых можно интерпретировать двоичным нулем или единицей. В восьми разрядах, например, можно закодировать 28=256 различных целых двоичных чисел - от 00000000 до 11111111, что достаточно для того, чтобы дать уникальное 8-битовое обозначение всем символам, необходимым для набора текста. Количество элементов, которые можно закодировать словами длины n, состоящими из символов из m-элементного алфавита, мощности m (мощность алфавита - это число символов в нем), равна N = mn. Если алфавит - {0,1}, то есть n = 2, то N= 2n.
Представление текстовой информации в ЭВМ.
Любое сообщение на любом языке состоит из последовательности символов — букв, цифр, знаков. Действительно, в каждом языке есть свой алфавит из определенного набора букв (например, в русском- 33 буквы, английском- 26, и т.д.). Из этих букв образуются слова, которые в свою очередь, вместе с цифрами и знаками препинания образуют предложения, в результате чего и создается текстовое сообщение. Не является исключением и язык, на котором «говорит» компьютер, только набор букв в этом языке является минимально возможным.
Стандартный набор из 256 символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией).
Он включает в себя большие и маленькие русские и латинские буквы, цифры, знаки препинания и арифметических действий и т.п.
Каждому символу ASCII соответствует 8-битовый двоичный код, например:
А — 01000001,
В — 01000010,
С — 01000011,
D — 01000100,
и т.д.
Таким образом, если человек создает текстовый файл и записывает его на диск, то на самом деле каждый введенный человеком символ хранится в памяти компьютера в виде набора из восьми нулей и единиц. При выводе этого текста на экран или на бумагу специальные схемы - знакогенераторы видеоадаптера (устройства, управляющего работой дисплея) или принтера образуют в соответствии с этими кодами изображения соответствующих символов.
Набор ASCII был разработан в США Американским национальным институтом стандартов (ANSI), но может быть использован и в других странах, поскольку вторая половина из 256 стандартных символов, т.е. 128 символов, могут быть с помощью специальных программ заменены на другие, в частности на символы национального алфавита, в нашем случае - буквы кириллицы.
Представление графической информации в ЭВМ.
Как и любая другая информация в ЭВМ, графические изображения хранятся, обрабатываются и передаются по линиям связи в закодированном виде - т.е. в виде большого числа бит - нулей и единиц. Существует большое число разнообразных программ, работающих с графическими изображениями. В них используются самые разные графические форматы- т.е. способы кодирования графической информации. Расширения имен файлов, содержащих изображение, указывают на то, какой формат в нем использован, а значит какими программами его можно просмотреть, изменить (отредактировать), распечатать.
Несмотря на все это разнообразие, существует только два принципиально разных подхода к тому, каким образом можно представить изображение в виде нулей и единиц (оцифровать изображение).
При использовании растровой графики с помощью определенного числа бит кодируется цвет каждого мельчайшего элемента изображения - пикселя. Каждый из пикселей имеет свой цвет, в результате чего и образуется рисунок, аналогично тому, как из большого числа камней или стекол создается мозаика или витраж, из отдельных стежков - вышивка, а из отдельных гранул серебра - фотография. При использовании растрового способа в ЭВМ под каждый пиксель отводится определенное число бит, называемое битовой глубиной. Каждому цвету соответствует определенный двоичный код (т.е. Код из нулей и единиц). Например, если битовая глубина равна 1, т.е. Под каждый пиксель отводится 1 бит, то 0 соответствует черному цвету, 1 -белому, а изображение может быть только черно-белым. Если битовая глубина равна 2. т.е. Под каждый пиксель отводится 2 бита, 00- соответствует черному цвету, 01- красному , 10 - синему ,11- черному, т.е. в рисунке может использоваться четыре цвета. Далее, при битовой глубине 3 можно использовать 8 цветов, при 4 - 16 и т.д. Поэтому, графические программы позволяют создавать изображения из 2, 4, 8, 16 , 32, 64, ... , 256, и т.д. цветов. Понятно, что с каждым увеличением возможного количества цветов (палитры) вдвое, увеличивается объем памяти, необходимый для запоминания изображения (потому что на каждый пиксель потребуется на один бит больше).
Основным недостатком растровой графики является большой объем памяти, требуемый для хранения изображения. Это объясняется тем, что нужно запомнить цвет каждого пикселя, общее число которых может быть очень большим. Например, одна фотография среднего размера в памяти компьютера занимает несколько мегабайт, т.е. Столько же, сколько несколько сотен (а то и тысяч) страниц текста. Для работы с растровой графикой используется в основном программа Adobe Photoshop.
При использовании векторной графики в памяти ЭВМ сохраняется математическое описание каждого графического примитива - геометрического объекта (например, отрезка, окружности, прямоугольника и т.п.), из которых формируется изображение. В частности, для построения окружности достаточно запомнить положение ее центра, радиус, толщину и цвет линии. По этим данным соответствующие программы построят нужную фигуру на экране дисплея. Понятно, что такое описание изображения требует намного меньше памяти (в 10 - 1000 раз) чем в растровой графике, поскольку обходится без запоминания цвета каждой точки рисунка. Одной из наиболее популярных программ векторной графики является Corel DRAW.
Системы счисления
Системы счисления бывают позиционные и непозиционные. Пример непозиционной системы — римская. В настоящее время используются в основном позиционные системы. В позиционной системе счисления каждая цифра имеет свой «вес», то есть значение цифры зависит от ее расположения в записи числа.
Запись числа в позиционной системе представляет собой сокращенный вариант записи выражения:
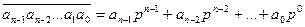 ,
,
где р - основание системы счисления, ai, – цифры (0 ≤ а i ≤ р-1).
Примеры.
1. Число 1 в обычной десятичной системе счисления означает один.
2. В числе 11 первая цифра справа означает 1, а вторая цифра справа — уже 10, поэтому число 11 означает 10+1, т. е. одиннадцать.
3. Рассуждая аналогично, получаем, что число 111 = 100 + 10 + 1, т. е. означает сто одиннадцать.
Основание системы счисления — это количество цифр позиционной системы счисления.
Позиционные системы отличаются друг от друга количеством цифр своего алфавита. Поэтому они именуется по своему основанию: десятичная, двоичная, троичная, восьмеричная, шестнадцатеричная и т.д.
Привычная нам десятичная система счисления имеет алфавит, состоящий из 10 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Пример. 512 = 5∙100+1∙10+2∙1. В числе 512 пять сотен, один десяток и две единицы.
Никаких преимуществ перед другими основаниями число 10 не имеет. Десятичная система кажется нам удобной только потому, что мы привыкли к ней с детства. В компьютерной технике более удобна двоичная система счисления.








