Краткая характеристика выборки и результатов эксперимента
| n | Муж | Жен | r | p | M | SD | min-max | |
| Мастера | 15 | 10 | 5 | 0,907 | 0,001 | 14,9 | 2,0 | 13–16 |
| Новички | 15 | 13 | 2 | 0,909 | 0,001 | 8,3 | 2,0 | 6–12 |
| 30 | 0,001 | t = 11,2 |
Анализ эксперимента (по Р. Солсо) [6].
Концепция автоматического характера кодирования частотности изложена в разд. А1. Поскольку авторов интересует оценка этого феномена на примере каратэ, возникает необходимость уделить внимание описанию ката каратэ А2. Рабочая гипотеза изложена в А3.
В разд. B приведена информация об испытуемых, используемом материале и процедурах.
Разд. C являет собой хороший пример описания процедуры: в нем излагается точный порядок происходивших событий.
Данные, полученные для обеих зависимых переменных (оценки частотности и свободного припоминания) описаны в разд. D 1; критерии внесения поправок в листы с ответами – в разд. D 2.
В разд. E 1 приведены общие результаты исследования. В E 2 дана дополнительная информация, касающаяся бесед с испытуемыми после эксперимента. В разделе «Обсуждение» приведена дополнительная информация, относящуюся к ходу эксперимента. Хотя понимание экспериментального контекста и не является частью фактической процедуры эксперимента, оно предоставляет информацию, с помощью которой можно лучше оценить полученные результаты. Возможные недостатки эксперимента описаны в разд. E 3, а в разд. E 4 приведены свидетельства, опровергающие возможное альтернативное объяснение. В разд. E 5 проведен анализ полученных данных.
Контрольные вопросы
1. Охарактеризуйте способ подбора групп (мастера и новички). Укажите на другие возможные способы подбора этих групп.
2. Экспериментаторами предполагалось, что испытуемые не обладали предварительными знаниями о кáта, с тем, чтобы его можно было принять за независимую переменную. Если бы кáта был знаком испытуемым, как это могло бы отразиться на результатах эксперимента? Имелась ли у авторов возможность удостовериться в том, что испытуемые не сталкивались ранее с данным набором приемов?
3. Как сказалась на эксперименте инструкция: «Пожалуйста, обратите особое внимание на кáта, который вы сейчас увидите, так как затем будет проверено, насколько хорошо вы запомнили использованные в нем приемы»? Можно ли было обойтись без этой инструкции? Следовало ли от нее отказаться?
4. Зачем испытуемых просили считать вслух по три в течение пяти минут, перед тем как они начали выполнять следующее задание?
5. Используя информацию из разд. E «Результаты», касающуюся припоминания, изобразите приблизительную гистограмму.
6. Какой вид деятельности может послужить основой для подобного эксперимента?

Таблица П 3.1
Критические значения р
(коэффициента корреляции
Спирмена для рангов)
| N | р = 0,05 | р = 0,01 |
| 5 | 1,000 | - |
| 6 | 0,886 | 1,000 |
| 7 | 0,786 | 0,929 |
| 8 | 0,738 | 0,881 |
| 9 | 0,683 | 0,833 |
| 10 | 0,648 | 0,794 |
| 12 | 0,591 | 0,777 |
| 14 | 0,544 | 0,715 |
| 16 | 0,506 | 0,665 |
| 18 | 0,475 | 0,625 |
| 20 | 0,450 | 0,591 |
| 22 | 0,428 | 0,562 |
| 24 | 0,409 | 0,537 |
| 26 | 0,392 | 0,515 |
| 28 | 0,377 | 0,496 |
| 30 | 0,364 | 0,478 |
Примечание. Таблица из [9].
Таблица П 3.2
Критические значения r
(коэффициента корреляции
Пирсона)
| df | Уровень значимости для проверки по двустороннему критерию | ||
| 0,10 | 0,05 | 0,01 | |
| 1 | 0,988 | 0,997 | 0,9999 |
| 2 | 0,900 | 0,950 | 0,990 |
| 3 | 0,805 | 0,878 | 0,959 |
| 4 | 0,729 | 0,811 | 0,917 |
| 5 | 0,669 | 0,754 | 0,874 |
| 6 | 0,622 | 0,707 | 0,834 |
| 7 | 0,582 | 0,666 | 0,798 |
| 8 | 0,549 | 0,632 | 0,765 |
| 9 | 0,521 | 0,602 | 0,735 |
| 10 | 0,497 | 0,576 | 0,708 |
| 11 | 0,476 | 0,553 | 0,684 |
| 12 | 0,458 | 0,532 | 0,661 |
| 13 | 0,441 | 0,514 | 0,641 |
| 14 | 0,426 | 0,497 | 0,623 |
| 15 | 0,412 | 0,482 | 0,606 |
| 16 | 0,400 | 0,468 | 0,590 |
| 17 | 0,389 | 0,456 | 0,575 |
| 18 | 0,378 | 0,444 | 0,561 |
| 19 | 0,369 | 0,433 | 0,549 |
| 20 | 0,360 | 0,423 | 0,537 |
| 25 | 0,323 | 0,381 | 0,487 |
| 30 | 0,296 | 0,349 | 0,449 |
| 35 | 0,275 | 0,325 | 0,418 |
| 40 | 0,257 | 0,304 | 0,393 |
| 45 | 0,243 | 0,288 | 0,372 |
| 50 | 0,231 | 0,273 | 0,354 |
| 60 | 0,211 | 0,250 | 0,325 |
| 70 | 0,195 | 0,232 | 0,303 |
| 80 | 0,183 | 0,217 | 0,283 |
| 90 | 0,173 | 0,205 | 0,267 |
| 100 | 0,164 | 0,195 | 0,254 |
Примечание. Таблица из [9].
Таблица П 3.3
Критические значения χ 2
| df | p | |
| 0, 05 | 0,01 | |
| 1 | 3,84 | 6,64 |
| 2 | 5,99 | 9,21 |
| 3 | 7,82 | 11,34 |
| 4 | 9,49 | 13,28 |
| 5 | 11,07 | 15,09 |
| 6 | 12,59 | 16,81 |
| 7 | 14,07 | 18,48 |
| 8 | 15,51 | 20,09 |
| 9 | 16,92 | 21,67 |
| 10 | 18,31 | 23,21 |
| 11 | 19,68 | 24,72 |
| 12 | 21,03 | 26,22 |
| 13 | 22,36 | 27,69 |
| 14 | 23,68 | 29,14 |
| 15 | 25,00 | 30,58 |
| 16 | 26,30 | 32,00 |
| 17 | 27,59 | 33,41 |
| 18 | 28,87 | 34,80 |
| 19 | 30,14 | 36,19 |
| 20 | 31,41 | 37,57 |
| 21 | 32,67 | 38,93 |
| 22 | 33,92 | 40,29 |
| 23 | 35,17 | 41,64 |
| 24 | 36,42 | 42,98 |
| 25 | 37,65 | 44,31 |
| 26 | 38,88 | 45,64 |
| 27 | 40,11 | 46,96 |
| 28 | 41,34 | 48,28 |
| 29 | 42,56 | 49,59 |
| 30 | 43,77 | 50,89 |
Примечание. Таблица из [9].
Таблица П 3.4
Критические значения t
| df | p | ||||
| 0,10 | 0,05 | 0,02 | 0,01 | 0,001 | |
| 1 | 6,314 | 12,706 | 31,821 | 63,657 | 636,619 |
| 2 | 2,920 | 4,303 | 6,965 | 9,925 | 31,599 |
| 3 | 2,353 | 3,182 | 4,541 | 5,841 | 12,924 |
| 4 | 2,132 | 2,776 | 3,747 | 4,604 | 8,610 |
| 5 | 2,015 | 2,571 | 3,365 | 4,032 | 6,869 |
| 6 | 1,943 | 2,447 | 3,143 | 3,707 | 5,959 |
| 7 | 1,895 | 2,365 | 2,998 | 3,499 | 5,408 |
| 8 | 1,860 | 2,306 | 2,896 | 3,355 | 5,041 |
| 9 | 1,833 | 2,262 | 2,821 | 3,250 | 4,781 |
| 10 | 1,812 | 2,228 | 2,764 | 3,169 | 4,587 |
| 11 | 1,796 | 2,201 | 2,718 | 3,106 | 4,437 |
| 12 | 1,782 | 2,179 | 2,681 | 3,055 | 4,318 |
| 13 | 1,771 | 2,160 | 2,650 | 3,012 | 4,221 |
| 14 | 1,761 | 2,145 | 2,624 | 2,977 | 4,140 |
| 15 | 1,753 | 2,131 | 2,602 | 2,947 | 4,073 |
| 16 | 1,746 | 2,120 | 2,583 | 2,921 | 4,015 |
| 17 | 1,740 | 2,110 | 2,567 | 2,898 | 3,965 |
| 18 | 1,734 | 2,101 | 2,552 | 2,878 | 3,922 |
| 19 | 1,729 | 2,093 | 2,539 | 2,861 | 3,883 |
| 20 | 1,725 | 2,086 | 2,528 | 2,845 | 3,850 |
| 21 | 1,721 | 2,080 | 2,518 | 2,831 | 3,819 |
| 22 | 1,717 | 2,074 | 2,508 | 2,819 | 3,792 |
| 23 | 1,714 | 2,069 | 2,500 | 2,807 | 3,768 |
| 24 | 1,711 | 2,064 | 2,492 | 2,797 | 3,745 |
| 25 | 1,708 | 2,060 | 2,485 | 2,787 | 3,725 |
| 26 | 1,706 | 2,056 | 2,479 | 2,779 | 3,707 |
| 27 | 1,703 | 2,052 | 2,473 | 2,771 | 3,690 |
| 28 | 1,701 | 2,048 | 2,467 | 2,763 | 3,674 |
| 29 | 1,699 | 2,045 | 2,462 | 2,756 | 3,659 |
| 30 | 1,697 | 2,042 | 2,457 | 2,750 | 3,646 |
| 60 | 1,671 | 2,000 | 2,390 | 2,660 | 3,505 |
| ∞ | 1,645 | 1,960 | 2,326 | 2,576 | 3,291 |
Примечание. Таблица из [9].
Таблица П 3.5
Критические значения F
| p=0,05 p=0,01 | Степени свободы для числителя dfbg | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | ∞ | ||
| Степени свободы для знаменателя dfwg | 1 | 161, 45 4032,10 | 199,50 4999,03 | 215,72 5403,49 | 224,57 5623,14 | 230,17 5764,08 | 233,97 5859,39 | 238,89 5981,34 | 243,91 6105,83 | 249,04 6234,16 | 254,32 6366,48 |
| 2 | 18,51 98,49 | 19,00 99,01 | 19,16 99,17 | 19,25 99,25 | 19,30 99,30 | 19,33 99,33 | 19,37 99,36 | 19,41 99,42 | 19,45 99,46 | 19,50 99,50 | |
| 3 | 10,13 34,12 | 9,55 30,81 | 9,28 29,46 | 9,12 28,71 | 9,01 28,24 | 8,94 27,91 | 8,84 27,49 | 8,74 27,05 | 8,64 26,60 | 8,53 26,12 | |
| 4 | 7,71 21,20 | 6,94 18,00 | 6,59 16,69 | 6,39 15,98 | 6,26 15,52 | 6,16 15,21 | 6,04 14,80 | 5,91 14,37 | 5,77 13,93 | 5,63 13,46 | |
| 5 | 6,61 16,26 | 5,79 13,27 | 5,41 12,06 | 5,19 11,39 | 5,05 10,97 | 4,95 10,67 | 4,82 10,27 | 4,68 9,89 | 4,53 9,47 | 4,36 9,02 | |
| 6 | 5,99 13,74 | 5,14 10,92 | 4,76 9,78 | 4,53 9,15 | 4,39 8,75 | 4,28 8,47 | 4,15 8,10 | 4,00 7,72 | 3,84 7,31 | 3,67 6,88 | |
| 7 | 5,59 12,25 | 4,74 9,55 | 4,35 8,45 | 4,12 7,85 | 3,97 7,46 | 3,87 7,19 | 3,73 6,84 | 3,57 6,47 | 3,41 6,07 | 3,23 5,65 | |
| 8 | 5,32 11,26 | 4,46 8,65 | 4,07 7,59 | 3,84 7,01 | 3,69 6,63 | 3,58 6,37 | 3,44 6,03 | 3,28 5,67 | 3,12 5,28 | 2,93 4,86 | |
| 9 | 5,12 10,56 | 4,26 8,02 | 3,86 6,99 | 3,63 6,42 | 3,48 6,06 | 3,37 5,80 | 3,23 5,47 | 3,07 5,11 | 2,90 4,73 | 2,71 4,31 | |
| 10 | 4,6 10,04 | 4,10 7,56 | 3,71 6,55 | 3,48 5,99 | 3,33 5,64 | 3,22 5,39 | 3,07 5,06 | 2,91 4,71 | 2,74 4,33 | 2,54 3,91 | |
| 11 | 4,84 9,65 | 3,98 7,20 | 3,59 6,22 | 3,36 5,67 | 3,20 5,32 | 3,09 5,07 | 2,95 4,74 | 2,79 4,40 | 2,61 4,02 | 2,40 3,60 | |
| 12 | 4,75 9,33 | 3,88 6,93 | 3,49 5,93 | 3,26 5,41 | 3,11 5,06 | 3,00 4,82 | 2,85 4,50 | 2,69 4,16 | 2,50 3,78 | 2,30 3,36 | |
| 14 | 4,60 8,86 | 3,74 6,51 | 3,34 5,56 | 3,11 5,03 | 2,96 4,69 | 2,85 4,46 | 2,70 4,14 | 2,53 3,80 | 2,35 3,43 | 2,13 3,00 | |
| 16 | 4,49 8,53 | 3,63 6,23 | 3,24 5,29 | 3,01 4,77 | 2,85 4,44 | 2,74 4,20 | 2,59 3,89 | 2,42 3,55 | 2,24 3,18 | 2,01 2,75 | |
| 18 | 4,41 8,28 | 3,55 6,01 | 3,16 5,09 | 2,93 4,58 | 2,77 4,25 | 2,66 4,01 | 2,51 3,71 | 2,34 3,37 | 2,15 3,01 | 1,92 2,57 | |
| 20 | 4,35 8,10 | 3,49 5,85 | 3,10 4,94 | 2,87 4,43 | 2,71 4,10 | 2,60 3,87 | 2,45 3,56 | 2,28 3,23 | 2,08 2,86 | 1,84 2,42 | |
| 25 | 4,24 7,77 | 3,38 5,57 | 2,99 4,68 | 2,76 4,18 | 2,60 3,86 | 2,49 3,63 | 2,34 3,32 | 2,16 2,99 | 1,96 2,62 | 1,71 2,17 | |
| 30 | 4,17 7,56 | 3,32 5,39 | 2,92 4,51 | 2,69 4,02 | 2,53 3,70 | 2,42 3,47 | 2,27 3,17 | 2,09 2,84 | 1,89 2,47 | 1,62 2,01 | |
| 40 | 4,08 7,31 | 3,23 5,18 | 2,84 4,31 | 2,61 3,83 | 2,45 3,51 | 2,34 3,29 | 2,18 2,99 | 2,00 2,66 | 1,79 2,29 | 1,52 1,82 | |
| 50 | 4,03 7,17 | 3,18 5,06 | 2,79 4,20 | 2,56 3,72 | 2,40 3,41 | 2,29 3,19 | 2,13 2,89 | 1,95 2,56 | 1,74 2,18 | 1,44 1,68 | |
| 60 | 4,00 7,08 | 3,15 4,98 | 2,76 4,13 | 2,52 3,65 | 2,37 3,34 | 2,25 3,12 | 2,10 2,82 | 1,92 2,50 | 1,70 2,12 | 1,39 1,60 | |
| 70 | 3,98 7,01 | 3,13 4,92 | 2,74 4,07 | 2,50 3,60 | 2,35 3,29 | 2,23 3,07 | 2,07 2,78 | 1,89 2,45 | 1,67 2,07 | 1,35 1,53 | |
| 80 | 3,96 6,98 | 3,11 4,88 | 2,72 4,04 | 2,49 3,56 | 2,33 3,26 | 2,21 3,04 | 2,06 2,74 | 1,88 2,42 | 1,65 2,03 | 1,32 1,49 | |
| 90 | 3,95 6,92 | 3,10 4,85 | 2,71 4,01 | 2,47 3,53 | 2,32 3,23 | 2,20 3,01 | 2,04 2,72 | 1,86 2,39 | 1,64 2,00 | 1,30 1,46 | |
| 100 | 3,94 6,90 | 3,09 4,82 | 2,70 3,98 | 2,46 3,51 | 2,30 3,21 | 2,19 2,99 | 2,03 2,69 | 1,85 2,37 | 1,63 1,98 | 1,28 1,43 | |
| 200 | 3,89 6,97 | 3,04 4,71 | 2,65 3,88 | 2,42 3,41 | 2,26 3,11 | 2,14 2,89 | 1,98 2,60 | 1,80 2,28 | 1,57 1,88 | 1,19 1,28 | |
| ∞ | 3,84 6,64 | 2,99 4,60 | 2,60 3,78 | 2,37 3,32 | 2,21 3,02 | 2,09 2,80 | 1,94 2,51 | 1,75 2,18 | 1,52 1,79 | 1,00 1,00 | |
Примечание. Таблица из [9].
Таблица П 3.6
Критические значения U-Манна-Уитни для независимых выборок
| n1 n2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 6 | 11 | 17 | |||||||||
| 6 | 7 | 12 | 18 | 26 | р = | 0,05 | ||||||
| 7 | 7 | 13 | 20 | 27 | 36 | |||||||
| 8 | 8 | 14 | 21 | 29 | 38 | 49 | ||||||
| 9 | 8 | 15 | 22 | 31 | 40 | 51 | 63 | |||||
| 10 | 9 | 15 | 23 | 32 | 42 | 53 | 65 | 78 | ||||
| 11 | 9 | 16 | 24 | 34 | 44 | 55 | 68 | 81 | 96 | |||
| 12 | 10 | 17 | 26 | 35 | 46 | 58 | 71 | 85 | 100 | 115 | ||
| 13 | 10 | 18 | 27 | 37 | 48 | 60 | 73 | 88 | 103 | 119 | 137 | |
| 14 | 11 | 19 | 28 | 38 | 50 | 63 | 76 | 91 | 106 | 123 | 141 | 160 |
| 15 | 11 | 20 | 29 | 40 | 52 | 65 | 79 | 94 | 110 | 127 | 145 | 164 |
| 16 | 12 | 21 | 31 | 42 | 54 | 67 | 82 | 97 | 114 | 131 | 150 | 169 |
| 5 | 15 | |||||||||||
| 6 | 10 | 16 | 23 | р = | 0,01 | |||||||
| 7 | 10 | 17 | 24 | 32 | ||||||||
| 8 | 11 | 17 | 25 | 34 | 43 | |||||||
| 9 | 6 | 11 | 18 | 26 | 35 | 45 | 56 | |||||
| 10 | 6 | 12 | 19 | 27 | 37 | 47 | 58 | 71 | ||||
| 11 | 6 | 12 | 20 | 28 | 38 | 49 | 61 | 74 | 87 | |||
| 12 | 7 | 13 | 21 | 30 | 40 | 51 | 63 | 76 | 90 | 106 | ||
| 13 | 7 | 14 | 22 | 31 | 41 | 53 | 65 | 79 | 93 | 109 | 125 | |
| 14 | 7 | 14 | 22 | 32 | 43 | 54 | 67 | 81 | 96 | 112 | 129 | 147 |
| 15 | 8 | 15 | 23 | 33 | 44 | 56 | 70 | 84 | 99 | 115 | 133 | 151 |
| 16 | 8 | 15 | 24 | 34 | 46 | 58 | 72 | 86 | 102 | 119 | 137 | 155 |
Примечание. Таблица из [5].
Таблица П 3.7
Критические значения W-критерия Вилкоксона для сопряженных пар
| n | р | n | р | |||
| 0,05 | 0,01 | 0,05 | 0,01 | |||
| 6 | 1 | 16 | 31 | 21 | ||
| 7 | 3 | 17 | 36 | 24 | ||
| 8 | 5 | 1 | 18 | 41 | 29 | |
| 9 | 7 | 3 | 19 | 47 | 33 | |
| 10 | 9 | 4 | 20 | 53 | 39 | |
| 11 | 12 | 6 | 21 | 60 | 44 | |
| 12 | 15 | 8 | 22 | 67 | 50 | |
| 13 | 18 | 11 | 23 | 74 | 56 | |
| 14 | 22 | 14 | 24 | 82 | 62 | |
| 15 | 26 | 17 | 25 | 90 | 69 | |
Примечание. Таблица из [17].
Таблица П 3.8
Линеаризующие преобразования
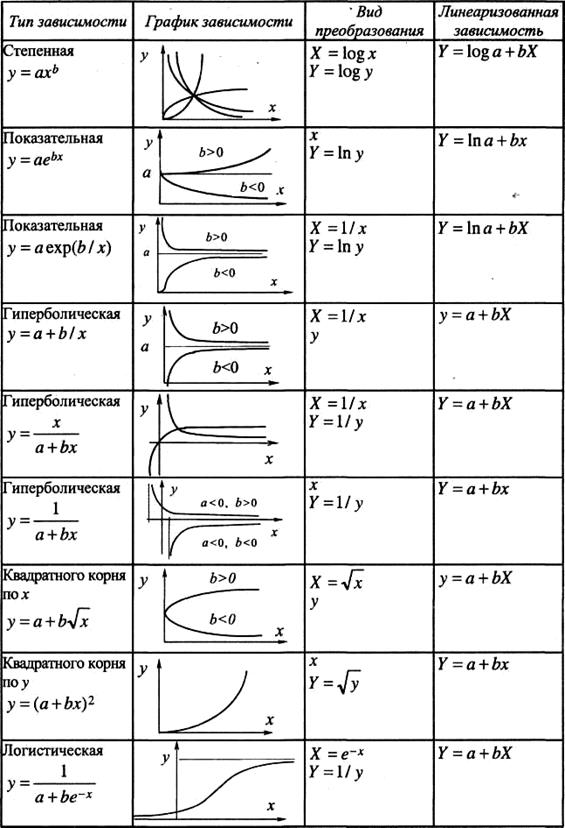
Примечание. Таблица из [1].
Литература
Основная
1. Большаков, А.А. Методы обработки многомерных данных и временных рядов: учеб. пособие / А.А. Большаков, Р.Н. Каримов. –М.: Главная линия – Телеком, 2007.
2. Вероятность и математическая статистика: Энциклопедия / под. ред. Ю.В. Прохорова. – М.: Большая Российская энциклопедия, 2003.
3. Воронов, И.А. Информационные технологии в физической культуре и спорте: учеб. Пособие / И.А. Воронов. – СПб.: СПбГУП, 2007.
4. Дюк, В.А. Информационные технологии в медико-биологических исследованиях / В.А. Дюк, В.Л. Эммануэль. – СПб.: Питер, 2003.








