5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
´Задача 3.9 [7]. Для решения требуется программа SPSS и файл данных MDS -2. sav. Квадратная симметричная матрица различий.
Преподавателю необходимо рассадить 12 учащихся в соответствии с результатами их тестирования по пяти показателям. Поскольку результаты тестирования не относятся к данным, характеризующим различия, необходимо сначала вычислить различия по имеющимся данным и таким образом свести задачу к предыдущей.
Исходные данные для этой задачи естественно представить в виде прямоугольной матрицы 12 × 5, в которой для каждого из 12 учащихся указаны результаты 5 тестов (файл MDS -2. sav). Затем по исходным данным строится квадратная (12 × 12) матрица различий между учащимися. Наконец, как и в предыдущем примере, SPSS создает матрицу координат 12 × 2 и визуально представляет ее в виде диаграммы.
Обратите внимание на два ключевых свойства матрицы различий: она является квадратной и симметричной. Несмотря на то, что исходная матрица является прямоугольной, т. е. ее строки (объекты) соответствуют учащимся, а столбцы (переменные) – тестам, в матрице различий как строки, так и столбцы соответствуют учащимся, и, следовательно, матрица является квадратной с размером 12 × 12. Далее, поскольку, к примеру, учащийся 1 отличается от учащегося 5 по результатам тестирования так же, как учащийся 5 от учащегося 1, матрица различий является симметричной.
В следующем примере демонстрируется двухмерное шкалирование квадратной симметричной матрицы различий, которую SPSS создает при задании переменных из файла данных. Данные матрицы различий имеют интервальный тип. В этом примере используется файл данных MDS -2. sav.
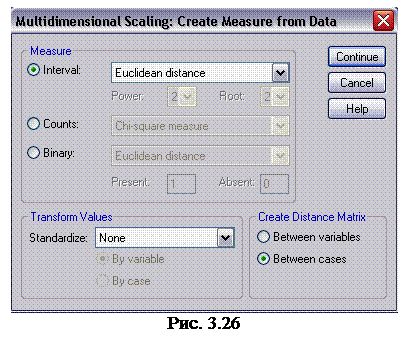
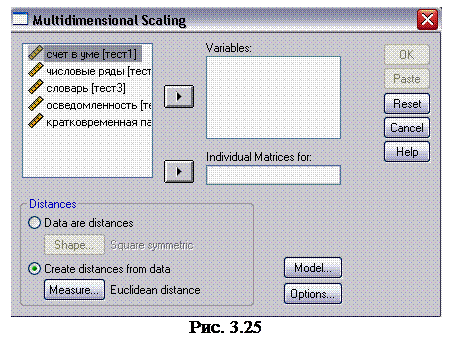 1. Откройте файл MDS -2. sav . В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные тест1 – тест5 в список Variables (переменные) (рис. 3.25).
1. Откройте файл MDS -2. sav . В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные тест1 – тест5 в список Variables (переменные) (рис. 3.25).
2. В группе Distances (расстояния) установите переключатель Create distances from data (вычислить расстояния по данным) и щелкните на кнопке Measure (мера), чтобы открыть диалоговое окно Multidimensional Scaling : Create Measure from Data (многомерное шкалирование: Создание меры для данных). В группе Create Distance Matrix (создание матрицы расстояний) установите переключатель Between cases (между объектами) и щелкните па кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.26).
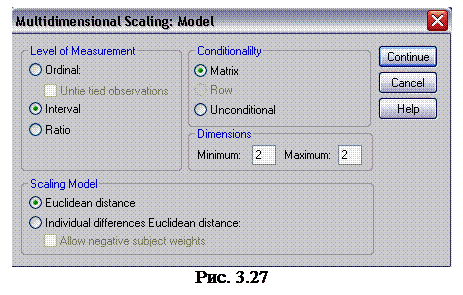
3. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling : Model (многомерное шкалирование: модель). В группе Level of Measurement (уровень измерения) установите переключатель Interval (интервальный) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.27).
 4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling : Options (многомерное шкалирование: Параметры). Установите флажок Group plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).
4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling : Options (многомерное шкалирование: Параметры). Установите флажок Group plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).
5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
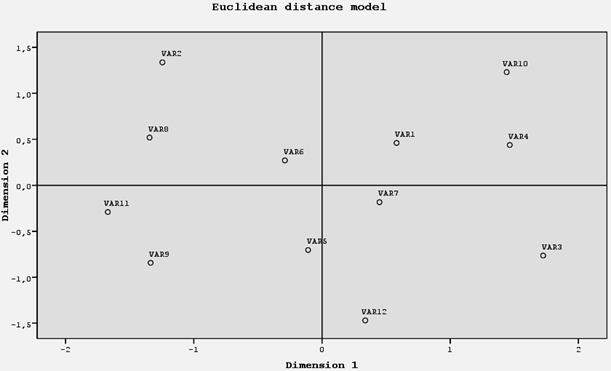
 ´Задача 3.10 [7]. Для решения требуется программа SPSS и файл данных MDS -3. sav. Пример двухмерного шкалирования с использованием квадратных симметричных матриц и модели индивидуальных различий. В обоих рассмотренных примерах создавалась единственная матрица различий, на основе которой вычислялись координаты точек-объектов для визуального представления. Однако в некоторых случаях возможно координатное представление нескольких матриц различий; примером может служить ситуация, когда несколько экспертов оценивают один и тот же набор объектов. В этих случаях говорят о ММШ индивидуальных различий.
´Задача 3.10 [7]. Для решения требуется программа SPSS и файл данных MDS -3. sav. Пример двухмерного шкалирования с использованием квадратных симметричных матриц и модели индивидуальных различий. В обоих рассмотренных примерах создавалась единственная матрица различий, на основе которой вычислялись координаты точек-объектов для визуального представления. Однако в некоторых случаях возможно координатное представление нескольких матриц различий; примером может служить ситуация, когда несколько экспертов оценивают один и тот же набор объектов. В этих случаях говорят о ММШ индивидуальных различий.
Шести студентам предложили сравнить между собой 5 многомерных статистических методов: множественный регрессионный анализ (МР), факторный анализ (ФА), кластерный анализ (КА), дискриминантный анализ (ДА) и многомерное шкалирование (МШ). Каждым студентом предъявляются все возможные пары из этих методов для оценки различия между ними (1 – максимально сходны, ..., 5 – максимально различны). Затем по данным для 6 студентов составляется 6 матриц различий (5×5 каждая).
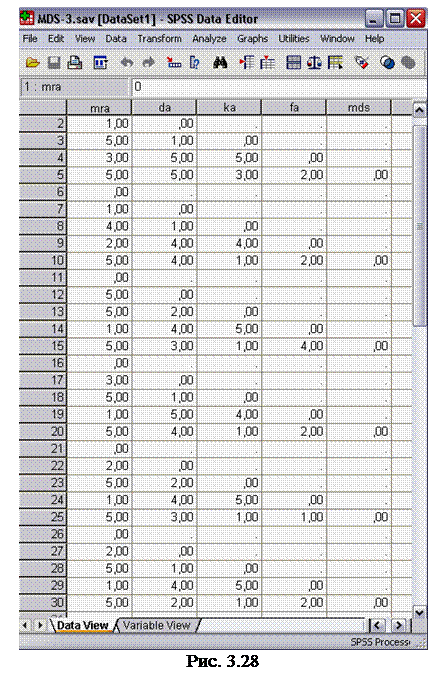
Поскольку SPSS предъявляет определенные требования к формату данных при использовании модели индивидуальных различий, был создан специальный файл MDS -3. sav (рис. 3.28). Требования к формату файла сводятся к наличию в этом файле нескольких квадратных матриц одинакового размера. В файле MDS -3. sav присутствует 6 матриц размером 5×5. Первые 5 строк файла соответствуют первой матрице, следующие 5 строк – второй матрице, и т. д. Всего под матрицы отведено 30 строк.
1. Откройте файл данных MDS -3. sav. В меню Analyze (анализ) выберите команду Sca - le ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные mra – mds в список Variables (переменные) (рис. 3.21).
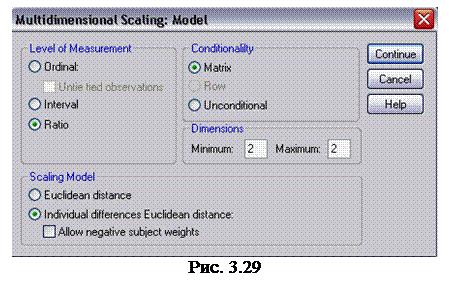
 2. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling : Model (многомерное шкалирование: модель), показанное на рис. 3.29. В группе Level of Measurement (уровень измерения) установите переключатель Ratio (отношение), а в группе Scaling Model (модель шкалирования) – переключатель Individual differences Euclidian distance (индивидуальные различия. Евклидово расстояние), после чего щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование).
2. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling : Model (многомерное шкалирование: модель), показанное на рис. 3.29. В группе Level of Measurement (уровень измерения) установите переключатель Ratio (отношение), а в группе Scaling Model (модель шкалирования) – переключатель Individual differences Euclidian distance (индивидуальные различия. Евклидово расстояние), после чего щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование).
3. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling : Options (многомерное шкалирование: параметры). Установите флажок Croup plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).
4. Щелкните на кнопке ОК, чтобы открыть окно вывода.
|
|
|
|
|
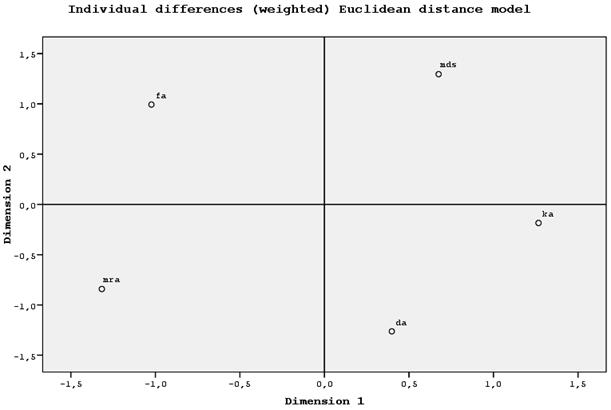
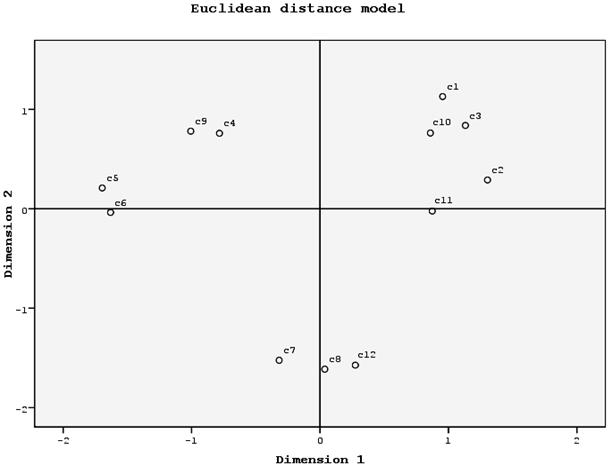
Dimension 1 (абсцисса) – слева расположены методы, основанные на корреляции, справа – на различиях по расстоянию.
Dimension 2 (ордината) – сверху структурные методы, снизу – методы предсказания.
Контрольные вопросы
1. Множественный регрессионный анализ (МР).
2. Факторный анализ (ФА).
3. Многомерное шкалирование (МШ).
4. Кластерный анализ (КА).
5. Дискриминантный анализ (ДА).
4. ТЕХНИКИ ЭКСПЕРИМЕНТОВ O , P , Q , R , S , T
В 1946 г. Р. Кеттелл предложил схемы эксперимента для выборок с малым n, названные «техника P» и «техника O» [27].
Техника P заключается в том, что одному испытуемому предъявляется не очень большое количество тестов, повторяющихся через некоторые интервалы времени и в результате получают «серию случаев». Обычно определяются корреляции между каждой парой таких «переменных», что дает коэффициенты, показывающие, в какой мере два теста (например, тесты на психологическую и физиологическую реакцию на стресс), выполняемые данным испытуемым в течение какого-то времени, характеризуются одинаковым колебанием результатов. В этом случае можно определить основные влияния, лежащие в основе этих колебаний и изменений, и характерные для индивидуальных особенностей испытуемого.
Техника P позволяет изучать: 1) индивидуальные, неповторимые свойства испытуемых; 2) их психосоматические связи.
Техника О применятся при исследовании одного испытуемого. Но в отличие от техники Р здесь коррелируют не тесты, выполняемые человеком в течение довольно большой серии случаев, а сами эти случаи. Например, используется большая серия тестов (не менее 20 – 25). С их помощью обследуется один человек в течение, скажем, m дней. Каждый день мы получаем какой-либо набор оценок из всех тестов серии. Здесь коррелируют не тесты, а дни.
Техника О является транспонированной к технике Р (табл. 4.1).
Таблица 4.1
| Тесты | Дни | |||||
| 1 | 2 | 3 | … | m | ||
| А | А 1 | А 2 | А 3 | А m | ||
| B | B1 | B2 | B3 | Bm | Строки, | |
| C | C1 | C2 | C3 | Cm | коррелирующие | |
| … | при технике Р | |||||
| N | N1 | N2 | N3 | Nm | ||
| Столбцы, коррелирующие при технике O | ||||||
Когда же речь заходит об экспериментах для выборок с большими n, применяют «технику R» и «технику Q».
 Техника R применяется при исследовании по возможности больших групп объектов с помощью одноразового единовременного тестирования признаков относительно небольшим количеством тестов. В этом случае определяют попарные взаимосвязи показателей признаков.
Техника R применяется при исследовании по возможности больших групп объектов с помощью одноразового единовременного тестирования признаков относительно небольшим количеством тестов. В этом случае определяют попарные взаимосвязи показателей признаков.
Техника Q исследует корреляции (или близости) между относительно небольшим количеством объектов, единовременно прошедших большую серию тестов. Полученные данные (коэффициент корреляции или расстояние) показывают, в какой мере два объекта одинаковы при выполнении одних и тех же тестов. Техника Q является транспонированной к технике R (табл. 4.2).
Таблица 4.2
| Испытуемые | Тесты | |||||
| (объекты) | 1 | 2 | 3 | … | m | |
| А | А 1 | А 2 | А 3 | А m | ||
| B | B1 | B2 | B3 | Bm | Строки, | |
| C | C1 | C2 | C3 | Cm | коррелирующие | |
| … | при технике Q | |||||
| N | N1 | N2 | N3 | Nm | ||
| Столбцы, коррелирующие при технике R | ||||||
Последнее время все чаще начинают применяться еще две техники, названные «техника S» и «техника T».
В технике S сопоставляются результаты двух испытуемых при выполнении одного теста в течение целой серии случаев. Она имеет особое значение для социальной психологии, поскольку может помочь при измерении сходства-различия реакций двух человек на идентичные задания в течение целой серии случаев. Исследование таких групп, состоящих из двух человек, как, например, близнецы, мужья и жены, руководители и их подчиненные и т. п., даст материал, с помощью которого можно будет изучить, насколько одинаково или неодинаково выполняли два человека определенные задания в данной серии случаев. Эта техника может иметь большое значение для эмпирического определения группы людей с учетом их реакции на задания или ситуации. Именно этим социальным аспектом объясняется обозначение техники буквой S (англ. social).
В технике Т сопоставляются два случая выполнения одного теста большой группой испытуемых. Она представляет собой попросту анализ надежности, определяемой для одного и того же теста и для тех же самых испытуемых в различных обстоятельствах. Много респондентов выполняют один и тот же тест два раза. Возникает вопрос: будут ли результаты первого испытания теми же, что и второго, т. е. будет ли группа людей, плохо выполнивших тест в первый раз, той же, что и группа людей, плохо выполнивших тест во второй раз? Техника T является транспонированной к технике S (табл. 4.3).
Таким образом, существуют три основные экспериментальные модели, каждая из которых включает две техники. Всего таких техник шесть. Каждая основная схема включает три главных элемента: «испытуемый объект», «тест» (задание) и «случай». В каждой такой схеме один из элементов является постоянным, а два остальных – переменными. Таким образом: а)
а) первая схема с техниками R и Q относится к одному случаю (случай – constant);
б) вторая схема с техниками О и Р относится к одному испытуемому;
в) третья схема с техниками S и Т относится к одному тесту.
Таблица 4.3
| Испытуемые | Случаи | |||||
| (объекты) | 1 | 2 | 3 | … | m | |
| А | А 1 | А 2 | А 3 | А m | ||
| B | B1 | B2 | B3 | Bm | Строки, | |
| C | C1 | C2 | C3 | Cm | коррелирующие | |
| … | при технике S | |||||
| N | N1 | N2 | N3 | Nm | ||
| Столбцы, коррелирующие при технике T | ||||||
Техники Р и S используют серию случаев, техники О и Q – серию тестов, техники R и Т – группу испытуемых.
В техниках Р и R коррелируют тесты, О и Т – случаи, Q и S – испытуемые объекты.
Таблица 4.4
| Техника | Исследуют | Применяют | Коррелируют | Строки-столбцы |
| O | 1 испытуемого | Серию тестов | Случаи | ║ |
| P | Серию случаев | Тесты | ═ | |
| Q | 1 случай | Серию тестов | Испытуемые | ═ |
| R | Группу испытуемых | Тесты | ║ | |
| S | 1 тест | Серию случаев | Испытуемые | ═ |
| T | Группу испытуемых | Случаи | ║ |
Контрольные вопросы
1. Техника эксперимента типа «O».
2. Техника эксперимента типа «P».
3. Техника эксперимента типа «Q».
4. Техника эксперимента типа «R».
5. Техника эксперимента типа «S».
6. Техника эксперимента типа «T».
7. Какими техниками эксперимента исследуется объект?
8. Какими техниками эксперимента исследуются условия?
9. Какими техниками эксперимента исследуется методика?
Приложение 1
Пример экспериментального плана с малым объемом выборки








